2. 广东工业大学土木与交通工程学院, 广州, 510006
2. School of Civil and Transportation Engineering, Guangdong University of Technology, Guangzhou, 510006, China
分类(Classification)[1]是从一个数据集(例如体检时测得的身高、体重、血糖、血压等数据)到一组预先定义的、非交叠的类别(例如正常、异常)的映射过程,主要包含映射关系的生成(即分类器的选取、建立和训练)和映射关系的应用(即用分类器判定新数据的类别)。模式识别、机器学习和数据挖掘等领域已经研究出种类繁多的分类器(或者分类算法)[2-4],而在实际应用中这些分类器的分类准确率主要取决于数据的内在特点。因此,如何根据数据的特点选取合适且有效的分类器成为分类成败的关键,同时也是数据挖掘研究领域急需解决的一个难题[5]。对于实际的分类任务,分类器的选取一般采用试错法(Trial-and-error strategy),即将不同种类的分类器分别尝试,最终选取分类准确率最高的那个。用试错法选取分类器十分耗时低效,计算代价极高。在2002年,Ho和Basu首次正式提出分类复杂度的概念[6],并在总结相关研究工作的基础上提出分类复杂度的量化模型及其计算方法[7]。该模型面向两类分类问题,以训练数据集为基础,通过评估数据在类别混叠、几何分布和分类边界等方面的特性来衡量分类问题的难易程度,从而对分类算法的选择提供有效的指导。此后,多位学者对Ho的分类复杂度量化模型进行了改进和补充[8, 9]。类别混叠度是分类复杂度的一种,它从几何统计和信息论两个角度定量地衡量数据分类的难易程度。利用类别混叠度指标,可以降低选取分类器过程中代价极高的盲目试错行为,在类别均衡的分类问题中得到了成功应用[10, 11]。
真实世界中广泛存在非均衡数据,这些数据在类别分布上通常具有非均衡性,即不同类别的数据在样本数量上差别较大,而且分类的重点是保证小类的准确率(即数据量少的小类更重要)[12]。例如,在人体的健康监测中,生理指标正常的数据占绝大多数,异常的数据只占很小的比例,而监测的重点就是要识别这些异常数据,以达到疾病预警的目的。在网络入侵检测中,极少量的黑客攻击数据淹没在海量的常规访问流量数据中,而检测的目的就是要识别出有攻击嫌疑的数据,以保证网络系统的信息安全。对于分类问题,类别分布不均衡往往会严重降低分类器的实际性能,极端情况下会使分类器失效,因此非均衡数据的分类器选取比均衡数据更加困难[13]。虽然分类复杂度(含类别混叠度)能够衡量类别均衡数据的分类难易程度,为分类算法的选取提供有效信息,但是对于非均衡数据,分类复杂度量化指标是否依然有效则需要进一步研究[14]。本文作者等通过在非均衡仿真数据上的实验研究,发现基于几何统计的类别混叠度指标的有效性会随着数据非均衡程度的加剧而减弱[15, 16]。在此基础上,需要更深入地研究其它的类别混叠度指标对非均衡数据的有效性,分析数据的非均衡程度对类别混叠度的影响规律,找出类别混叠度指导非均衡数据分类的有效方法。
本文在已有的研究基础上,采用实验研究的方法,验证类别混叠度量化指标指导非均衡数据分类的有效性,以减少甚至避免盲目试错带来的庞大计算开销。本文的主要贡献有:(1)针对两类分类问题,设计验证实验,在非均衡仿真数据上研究类别混叠度(基于几何统计和信息论两类衡量指标)的有效性;(2)在实验研究的基础上,分析数据的非均衡性对类别混叠度的影响规律,找出类别混叠度指导非均衡分类的有效方法;(3)在真实的非均衡数据上验证类别混叠度指导非均衡分类的实际效果。
1 非均衡数据与类别混叠度本节先介绍数据的非均衡率,然后讨论类别混叠度的概念及其量化指标。
1.1 数据的非均衡率真实世界中许多数据在类别分布上具有非均衡性,即不同类别的数据在样本数量上差别较大,其中数据量大的那类称为大类,反之则为小类。在非均衡分类问题中,分类的重点一般是保证小类的准确率,即数据量少的小类更重要。类别分布不均衡往往会严重降低分类器的实际性能,极端情况下会使分类器失效,因此非均衡数据的分类器选取比常规的均衡数据更加困难。
非均衡率(Imbalance ratio,IR)是大类样本数量与小类样本数量的比例,如下
| $ {\rm{IR}} = \frac{{{N_1}}}{{{N_2}}} $ | (1) |
式中: N1为大类样本数,N2为小类样本数。
IR用以衡量数据非均衡的严重程度,IR值越大,大类与小类的样本数量相差越悬殊,非均衡性也越强。一般来讲,IR>9的数据属于非均衡程度严重的数据[17]。
1.2 类别混叠度及其量化指标类别混叠度,又名数据混淆度(Cla ss overlap of data, COD)[16, 18], 是指不同类别数据之间互相交叠、混合的程度。混叠度越高,分类的难度越大。常用的类别混叠度量化指标包括基于几何统计的和基于信息论的两大类,前者用单个特征在不同类别取值区间的交叠程度来衡量,而后者则用单个特征能够给分类提供的信息量来衡量。本文采用的类别混叠度指标如表 1所示。
| 表 1 类别混叠度指标 Tab. 1 Measures of class overlap of data |
表 1中,F1,F2,F3,I1和I2的取值范围均为[0, 1]。其中,F1,F2和F3从几何统计的角度来衡量类别混叠度,而I1和I2从信息论的角度来衡量类别混叠度,它们的计算方法详见文献[18, 19]。
根据几何统计理论,F1衡量单个特征的类间差异占该特征的总差异(类间差异与类内差异之和)的比例,低的F1值表明类间差异比重较小,数据的混叠程度较严重;针对单个特征,F2衡量两类数据的交集与并集的比例,高的F2值表明交集比重较大,数据的混叠程度较严重;F3衡量单个特征对分类的贡献程度,低的F3值表明该特征对分类的贡献度较小,数据的混叠程度较严重。根据信息论的原理,I1和I 2衡量单个特征能够给分类提供的信息量,低的I1和I2值表明提供的信息量较少,数据的混叠程度较严重。
2 类别混叠度的有效性研究方法本节先介绍类别混叠度有效性验证实验的总体方案,然后分析仿真数据生成的关键因素,最后介绍所采用的真实数据。
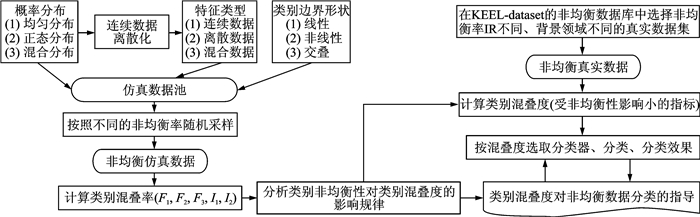
2.1 总体方案如图 1所示,本文采用的实验验证方法主要包括以下8个步骤:
|
图 1 实验研究方案流程图 Fig. 1 Evaluation pocedure |
(1) 生成仿真数据池,含不同特征类型(连续数据、离散数据、混合数据)、不同概率分布(均匀分布、正态分布、混合分布)、不同边界形状(线性边界、非线性边界、边界上不同类别数据交叠)的数据;
(2) 分别以不同的非均衡率IR对仿真数据进行随机采样,得到非均衡性各异的仿真数据;
(3) 计算混叠度指标F1, F2, F3, I1, I2;
(4) 通过F-test检验上述5个指标受IR影响的程度,分析受影响的规律,;
(5) 根据步骤(4)中的结论,找出对IR具有较强鲁棒性的指标;
(6) 根据步骤(4)中的结论,找出对分类的指导信息;
(7) 从KEEL-dataset数据库中选择IR不同、背景领域不同的非均衡真实数据;
(8) 根据步骤(6)中得到的指导信息,用步骤(5)中得到的鲁棒性较强的混叠度指标,指导真实数据分类,评价分类效果,验证从仿真数据实验中得到结论的实际有效性。
2.2 仿真数据为了研究混叠度对非均衡数据的有效性,本文借鉴前期工作[15-16, 18],生成了不同特征类型、不同概率分布、不同类别边界、不同非均衡率的仿真数据。每个仿真数据集含4个特征变量和1个类别变量。特征变量的概率分布公式和类别边界的判别函数如表 2所示。
| 表 2 特征变量的概率分布、类别边界形状及判别函数 Tab. 2 Probability distribution of explanatory variables, boundary shapes and decision functions |
2.3 真实数据
本文从国际公共数据库KEEL-dataset[17]中选取背景领域不同、特征类型不同、非均衡率IR取值介于1~130之间的10个真实数据集,用于验证仿真数据实验结果的实际有效性。真实数据集的具体信息见表 3所示。
| 表 3 非均衡真实数据 Tab. 3 Real-world imbalanced data |
3 实验与结果分析
本节首先介绍验证实验的关键配置,然后分析仿真数据的实验结果,最后讨论真实数据的实验结果。
3.1 实验配置本文的实验按照图 1所示的流程进行。在步骤(1)中,仿真数据的正态分布取N (0, 1), 均匀分布取U(-3, +3),连续数据离散化采用无监督学习的等距分箱法[18],数据池中的样本数为3 000 000。在步骤(2)中,分别按照IR=1, 3, 7, 9, 19, 24, 49, 99共8个等级随机采样,生成非均衡率不同、数据类型不同、概率分布不同、边界形状不同的数据集,共计120个,每个数据集含10000个样本。在步骤(4)中,F-test检验取置信度α=5%。在实验中,仿真数据的生成算法、类别混叠度量化指标的计算方法、真实数据的分类算法均用MATLAB实现。单个混叠度指标的变化率按式(2)计算
| $ 变化率 = \frac{{\left| {{\rm{IR}}为99时的值 - {\rm{IR}}为1时的值} \right|}}{{\;\;\;\;\;{\rm{IR}}为1时的值\;\;\;\;\;\;\;\;\;\;\;}} \;\;\; \times 100\% ,\;其中\left| \cdot \right|表示绝对值 $ | (2) |
类别混叠度有效性的实验研究在120个非均衡仿真数据集上进行,共获得15组实验结果。因篇幅限制,本文仅给出其中的3组结果,即混叠度在混合数据加混合分布上随IR变化的情况,具体如表 4所示。15组实验结果中的混叠度变化率与对应的数据情况之间的关系如表 5所示。
| 表 4 混叠度随IR变化的情况(混合数据加混合分布) Tab. 4 COD under different IR (mixed variables plus composite distributions) |
| 表 5 不同数据情况下的混叠度变化率 Tab. 5 COD change rate with different data characteristics |
综合分析仿真数据集上的实验结果,可以得出类别混叠度的量化指标对非均衡数据适应性的结论如下:
(1) 随着非均衡度IR的增加,混叠度指标都会受到不同程度的影响;
(2) 当非均衡度IR发生变化时,在不同的类别边界形状(线性、非线性、交叠)、不同的数据类型(连续、离散、混合)、不同的概率分布(正态分布、均匀分布、混合分布)下,混叠度的变化程度差别较大,其中,类别边界形状是影响最严重的一个因素。
(3) 当类别边界无交叠混合或者交叠混合轻微(即数据在现有特征空间可分)时,随着非均衡率IR的增加,F1是所有指标中变化率最小的;当类别边界交叠混合严重时(即数据在现有特征空间不可分),I2是所有指标中变化率最小的。
(4) 对于F1,当类别边界无交叠混合或者交叠混合轻微时,随着非均衡率IR的增加,其变化率在不同的数据类型、不同的概率分布下差别较小(10%以内)。
(5) 对于I2,当类别边界交叠混合严重时,随着非均衡率IR的增加,其变化率在不同的概率分布、不同的数据类型下,差别相对有些大(50%以内)。
进一步分析上述结论,可以得到如下信息:
(1) 对于类别非均衡数据,可以选用F1和I2两个混叠度指标进行分类指导;
(2) 如果知道类别边界的大致形状,当类别边界无交叠混合或者交叠混合轻微,可以选择F1指导分类;当类别边界交叠混合严重时,可以选择I2指导分类;
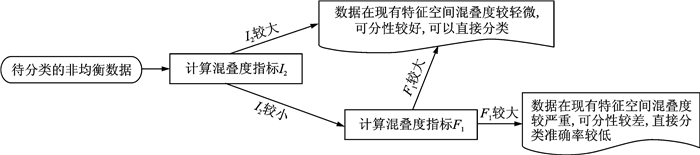
(3) 对于实际的非均衡分类问题,一般无法在分类前知道类别边界的情况,只能根据IR,F1,I2来指导分类,如图 2所示主要包含以下步骤:
|
图 2 F1和I2指导非均衡数据分类的信息 Fig. 2 Guidelines of F1 and I2 to classify imbalanced data |
(3a) 计算非均衡数据的I2,如果I2较大,执行步骤(3b), 如果I2较小,执行步骤(3c);
(3b) 对非均衡数据分类,准确率较高;
(3c) 计算F1,如果F1较大,对非均衡数据分类;如果F1较小,直接分类准确率较低。
3.3 真实数据的实验结果与分析本文采用表 3列出的10个真实的非均衡数据集,验证图 2所示的分类指导信息的实际有效性。取F1> 0.6为较大,I2>0.2为较大,采用经典的贝叶斯分类器,经过5-Folds的交叉验证,实验结果如表 6所示。
| 表 6 F1和I2指导非均衡真实数据分类 Tab. 6 Classification of real-world imbalanced data with the guidelines of F1 and I2 |
在表 6中,序号为2和3的数据集I2>0.2,按照图 2中的指导信息,直接分类,且准确率高于90%。序号为1, 4, 5, 6, 7, 8, 9, 10的数据集I2 < 0.2,按照图 2所示需要进一步计算F1。序号为4, 5, 7, 9的数据集F1>0.6,直接分类,且准确率高于90%。序号为1, 6, 8, 10的数据集F1 < 0.6,直接分类得到的准确率均较低。综上所述,在仿真数据上总结出的类别混叠度指导非均衡数据分类的信息,在真实的非均衡数据分类中是有效的。
本文采用的5个混叠度量化指标F1, F2, F3, I1和I2都是在单个特征的维度上衡量非均衡数据的最大混叠程度,其中对数据的非均衡率具有较强鲁棒性的F1和I2用来指导非均衡数据的分类。因为是从单个特征的角度衡量混叠度,所以特征维度的高低只影响计算开销的大小。因此,本文的验证实验所得的结论对高维的非均衡数据是有效的。
4 结束语类别混叠度衡量不同类别数据之间互相交叠、混合的程度,其量化指标包含基于几何统计的和基于信息论的两类,可以用来指导均衡数据的分类。在实际的分类问题中,存在大量非均衡的数据。本文通过实验研究,验证了类别混叠度量化指标会随着数据非均衡性的增加而发生变化。在所研究的5个混叠度指标中,F1是基于几何统计的指标中受影响最小的,I2是基于信息论的指标中受影响最小的。通过仿真数据和真实数据上的实验结果,F1和I2可以用来指导非均衡数据的分类。
本文的工作可以从两个方面加以改进:(1)选取更多的非均衡数据验证类别混叠度的有效性,包括不同应用背景、不同数据类型和特征维度更高的非均衡数据集;(2)改进现有的混叠度量化指标,使其具有更强的鲁棒性,能够适用于极端非均衡率的情况。
| [1] |
Witten I H, Frank E, Hall M A, et al. Data ming:Practical machine learning tools and techniques[M]. 4th ed. [S.l.]: Elsevier Inc, 2016.
|
| [2] |
Liao S H, Chu P H, Hsiao P Y. Data mini ng techniques and applications-A decade review from 2000 to 2011[J]. Expert Systems with Applications, 2012, 39: 11303-11311. DOI:10.1016/j.eswa.2012.02.063 |
| [3] |
邸鹏, 段利国. 一种新型朴素贝叶斯文本分类算法[J]. 数据采集与处理, 2014, 29(1): 71-75. Di Peng, Du an Liguo. New naive Bayes text classification algorithm[J]. Journal of Data Acqu isition and Processing, 2014, 29(1): 71-75. DOI:10.3969/j.issn.1004-9037.2014.01.010 |
| [4] |
李亚克, 田青, 高航. 结合类标签关联度的有序核判别回归学习[J]. 数据采集与处理, 2016, 31(3): 532-540. Li Yake, Tian Qing, Gao Hang. Kernel discriminant learning for ordinal regression using label membership[J]. Journal of Data Acquisition and Processing, 2016, 31(3): 532-540. |
| [5] |
Kotsiantis S B. Supervised ma chine learning:A review of classification techniques[J]. Informatica, 2007, 31: 249-269. |
| [6] |
Ho T K, Basu M. Complexity measures of supervised classification problems[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(3): 289-300. DOI:10.1109/34.990132 |
| [7] |
Ho T K, Basu M, Law M H C. Data complexity in pattern recognition[M]. London: Springer-Verlag, 2006: 1-23.
|
| [8] |
Kwon O, Sim J M. Effects of data set features on the performances of classification algorithms[J]. Expert Systems with Applications, 2013, 40: 1847-1857. DOI:10.1016/j.eswa.2012.09.017 |
| [9] |
Macià N, Bernadó-Mansilla E, Orriols-Puig A, et al. Learner excellence biased by data set selection:a case for data characterisation and artificial data sets[J]. Pattern Recognition, 2013, 46: 1054-1066. DOI:10.1016/j.patcog.2012.09.022 |
| [10] |
Sotoca J M, Sánchez J S, Mollineda R A. A review of data complexity measures and their applicability to pattern classification problems[C]//Proceedings of the A ctas del Ⅲ Taller Nacional de Mineria de Datosy Aprendizaje, TAMIDA 2005. Granada, Spain: Thomson, 2005: 77-83.
|
| [11] |
Cano J R. Analysis of data complexity measures for classification[J]. Expert Systems with Applications, 2013, 40(12): 4820-4831. DOI:10.1016/j.eswa.2013.02.025 |
| [12] |
Guo H, Li Y, Shang J, et al. Learning from class-imbalanced data:Review of methods and applications[J]. Expert Systems with Applications, 2017, 73: 220-239. DOI:10.1016/j.eswa.2016.12.035 |
| [13] |
López V, Fernández A, García S, et al. An insight into classification with imbalanced data:Empirical results and current trends on using data intrinsic characteristics[J]. Information Sciences, 2013, 250: 113-141. DOI:10.1016/j.ins.2013.07.007 |
| [14] |
Anwar N, Jones G, Ganesh S. Measurement of data complexity for classification problems with unbalanced data[J]. Statistical Analysis and Data Mining, 2014, 7: 194-211. DOI:10.1002/sam.11228 |
| [15] |
Xing Y, Cai H, Cai Y, et al. Preliminary evaluation of classification complexity measures on imbalanced data[C]//Proceedings of the 2013 Chinese Intelligent Automation Conference. Yang zhou, China: Springer: 2013: 189-196.
|
| [16] |
刘锟, 非均衡数据几何复杂度及其应用研究[D].广州: 东工业大学, 2012. Liu Kun. Research on measures of geometrical complexity in imbalanced classification problems and its application[D]. Guangzhou: Guangdong University of Technology, 2012. 非均衡数据几何复杂度及其应用研究 |
| [17] |
Alcalá-Fdez J, Ferná ndez A, Luengo J, et al. KEEL data-mining software tool:Data set repository, integration of algorithms and experimental analysis framework[J]. Journal of Multiple-Valued Logic and Soft Computing, 2011, 17: 255-287. |
| [18] |
贾小彦.类别非均衡性对数据混淆度影响的研究[D].广州: 广东工业大学, 2016. Jia Xiaoyan. The effects of data imbalance on the performance of data complexity measures[D]. Gu angzhou: Guangdong University of Technology, 2016. http://cdmd.cnki.com.cn/Article/CDMD-11845-1016156803.htm |
| [19] |
Orriols-Puig A, Maci à, Ho T K. Documentation for the data complexity library in C++. G RSI Report No. 2010001[R]. http://www.nuriamacia.com/files/DocumentationDCoL10.pdf, 2010.
|
 2018, Vol. 33
2018, Vol. 33

