2. 南通理工学院计算机与信息工程学院, 南通, 226002
2. School of Computer and Information Engineering, Nantong Institute of Technology, Nantong, 226002, China
基于图像的建模方法,由于其建模速度快、易操作和成本低等优点,逐渐成为计算机视觉和图形学界热点研究内容。图像包含丰富的几何场景信息和颜色信息,利用一组图像序列重建出三维立体点云模型,实现高逼真场景再展现,可应用于医学、考古和建筑等多个领域。由于输入图像包含复杂的背景环境,以及模型自身可能存在的凹几何遮挡等原因,重建出的点云模型会包含许多离群点。手动去噪过程不仅耗时耗力,而且无法批量、重复性处理多个点云模型。因此,迫切需要找到一种鲁棒的方法实现离群点自动检测和滤除。
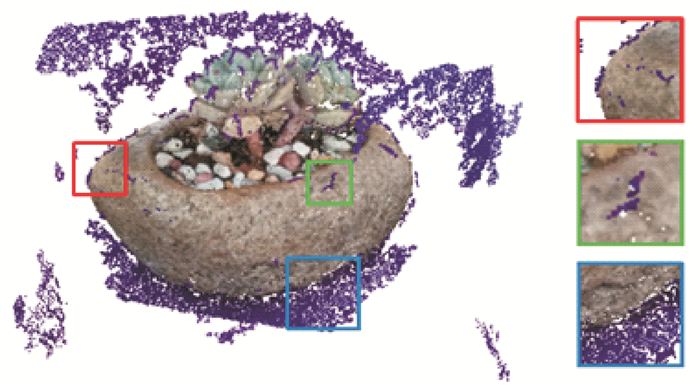
由于离群点的形成受多方面因素影响,所以离群点的分布无规律、无特定位置和状态。从局部密度来看,离群点可能孤立存在也可能形成高密度点簇。从空间位置来看,离群点可能远离模型主体,也可能围绕在模型周围甚至附着在模型表面。如图 1中Buddha模型所示,红色方框中表示的是距离模型主体较远的离群点簇,此类离群点簇单单根据空间距离来判断就很容易被检测和剔除。绿色方框中表示的是模型主体附近以及与附着在模型表面的离群点,这些离群点由于距离模型表面过近,很难同模型表面点云进行区分。蓝色方框中表示的是由于凹几何遮挡等原因,与模型主体分离的较小点簇,这些点簇同属模型表面有效点簇,如果只从空间位置关系度量来看,易被视为离群点簇而滤除。上述这些情况都给自动有效地检测离群点带来了巨大挑战。

|
图 1 Buddha模型中的离群点分布情况 Fig. 1 Outlier distribution in Buddha model |
常见的离群点检测算法有许多,根据离群点的分布状态,可从密度、聚类和空间距离等维度进行检测。如文献[1, 2]提出的基于距离的离群点检测方法,根据事先设定的空间距离阈值,将距离小于该阈值的两点归为同一个点簇。依据此方法,将点云模型分为数量大小不同的点簇,包含数据点数量最多的点簇视为模型所在的有效点簇,其他较小点簇则被视为离群点簇被滤除。此方法会错误地滤除与模型主体分离的较小有效点簇,同时,也无法正确识别与模型相连接以及附着在模型表面的离群点。K-近邻(K-nearest neighbor, KNN)算法[3]同样是依靠数据点之间空间距离关系来进行判断的方法。不同的是,该方法需要先人为设定离群点个数, 然后分别计算每个数据点与其第k个最近邻点的空间距离并进行排序,去距离最大的k个点作为离群点。该算法需要人为输入离群点数量,从视觉感官上很难精准估算每个模型中包含的离群点个数,而且,对于模型周围距离较近的离群点无法有效滤除。文献[4]提出的KNN改进算法,采用高斯影响函数作为核函数来估计当前测试点对周围邻近点的影响力,避免了人为判断离群点数量。遗憾的是,该算法只能检测孤立离群点,对于其他类型离群点同样不能有效检测。文献[5-7]基于密度的方法对离群点进行检测,首先对点云模型所在空间进行单元格划分,然后根据数据点所在单元格及其邻域内包含的点个数,来判断其是否为离群点。该方法适用于包含较少孤立离群点的点云模型,但在实际模型中,离群点不仅数量庞大,而且密集聚集在一起,无法通过邻域内数据点个数判断其离群程度。文献[8]中提出了一种表面传播方法,该方法认定点云模型表面能够形成平滑面片,而随机分布的离群点则不能。稀罕的是,此方法针对扫描仪建模等模型有效,基于图形的建模在许多时候同样会生成平滑的离群点簇。除此之外,许多平滑算法都被用来检测离群点。除上述算法之外,许多其他的平滑算法均被用来检测离群点,对于有序或部分有序的点云,可以用最小二乘滤波[9]、维纳滤波[10]和平滑滤波[11]等。对于散乱点云,可以用平均曲率流[12]、双边滤波器[13, 14]、移动最小二乘法[15-17]等方法。但是对于密集分布在一起且数量较大的离群点簇,以上算法都不能达到较好的检测效果。
本文提出了一种综合的离群点检测方法,能够有效检测距离模型主体较远的离群点、与模型表面相连以及附着在模型表面的离群点。针对不同的分布特点,采用不同的检测方法。其中,距离模型主体较远的离群点可通过空间距离进行判断;与模型主体距离较近的点簇通过边界匹配法,在保留有效数据点簇的同时滤除离群点簇;而对于与模型表面相连以及附着在模型表面的离群点,可通过基于RGB颜色值的聚类分析法结合已识别的离群点进行检测和滤除。
1 空间拓扑关系建立基于图像的三维重建,为保证重建点云模型的高精度和高逼真效果,输入的图像序列往往多达数十张,重建出的点云模型包含几十万乃几百万个数据点。当建模对象所处的背景复杂或背景颜色与模型相近时,重建出的点云模型会包含大量离群点。这些离群点可能分布在点云模型所在空间各个地方。因此,在离群点检测过程中,需要遍历所有数据点,这无疑会消耗大量运算时间。为了加快相邻数据点搜索速度,首先需要在点云模型所在的空间构建空间拓扑关系。
针对基于图像重建出的点云模型,通过单元格划分法对点云所在最小空间进行划分,将所有数据点划分至不同的单元格中,以此来确定数据点之间空间拓扑关系。
假设点云模型中共包含N个数据点,最小包围盒体积为V。如果单元格设置太大,则无法有效识别距离模型表面较近的离群点,同时,每个单元格包含数据点的数量增多,单元格内数据点的搜索速度相应下降;如果单元格过小,则会降低单元格的搜索速度,所以需要首先确定单元格边长cell_size。单元格边长可以通过模型的V和N的大小关系得到,即
| $ {\rm{cell}}\_{\rm{size}} = r\sqrt[3]{{V/N}} $ | (1) |
式中:r为调节因子,该边长大小反映了点云数据在空间中的分布情况。
根据已知的单元格边长,平行于坐标轴分别对点云空间进行划分,可得到m×n×l个小单元格。划分单元格后,利用哈希表法构造数据点与存储位置之间的映射关系。对于点云模型中任意一点P(Px, Py, Pz),根据其所在单元格索引以及在单元格内部的索引序号,能够快速定位找到该数据点和它的邻域。
在划分好的最小包围盒空间中,认定位置相邻且非空的单元格属于同一个连通域,连通域内,单元格包含的所有数据点属于同一个点簇。基于上述定义,可以得到多个大小不同的连通域,已知最大的单元格连通域包含点云模型主体部分,其他距离模型主体较远的连通域视为离群点簇所在连通域,从而被滤除。
由于重建点云模型中,存在距离模型主体过远的离群点,使得最小包围盒体积过大,单元格划分后的空单元格较多。求最大连通域的目的是为滤除那些远离模型主体的离群点,减少空单元格数量,避免每个单元格内包含的数据点过多或过少,从而加快数据点搜索速度。在滤除位置较远的离群点后,可以根据需要对最小包围盒进行重新划分,边长cell_size相应缩小。在后续求点簇的操作中,同属一个连通域内的所有数据点被当做一个点簇处理。
2 有效点簇检测建模对象可能存在的凹几何结构遮挡,或者模型表面光线反射等因素会造成重建点云模型表面部分区域数据点稀疏甚至是空洞现象,从而导致模型表面被分割为多个部分,较小点簇与最大点簇分离,而非理想的完整点簇。如果单单依靠空间距离进行判断,很容易将这些较小点簇错误地当做离群点滤除掉。由于这些较小的点簇和最大点簇一样,同属模型表面一部分,因此可以通过扩展其边界实现与最大点簇相连。与之相反,离群点簇不具有模型表面几何形状特征,在扩展边界的时候与最大点簇相连的可能性较低。综上,从距离最大点簇最近的较小点簇开始计算,依次进行边界匹配操作,如果匹配结果为有效点簇,则归入最大点簇。依据此方法能够区分点云中的有效点簇和离群点簇。
假设在同一平面上,点P是其所在数据点簇的边界点,易知P的k个近邻点分布偏向于P的同一侧。如果P为内部点,则k个近邻点将分布于P的各个方向。在三维空间中,点簇中所有点很难同时位于同一水平面上。所以,需要先将P的k个近邻点投影至点P所在的切平面,然后通过最大开角一致性[18]来判断P是边界点还是内部点。
假设在重建点云模型中,最大的点簇G是由模型主体表面数据点构成的有效点簇。按照与最大点簇距离的大小顺序,可采用边界匹配方法[19]将其他较小点簇依次与最大点簇进行对比。根据比对结果将较小有效点簇加入到最大点簇中,同时剔除离群点簇。具体比对过程如下:对于较小候选点簇中的任意一个边界点ci,在G中可以找到距离ci最近的一点gi。如果gi同样是G上的边界点,那么〈ci, gi〉就是C到G的一个边界匹配对。设m为簇C中边界点的总个数,n为C到G的匹配对个数,r(C, G)=m/n为C到G的边界匹配率,如果边界匹配率大于0.25(由经验给出),则认为C可以通过边界扩展与G相连,即C簇是由模型表面数据点组成的有效点簇,如果边界匹配率小于0.25,则认为C为离群点簇。
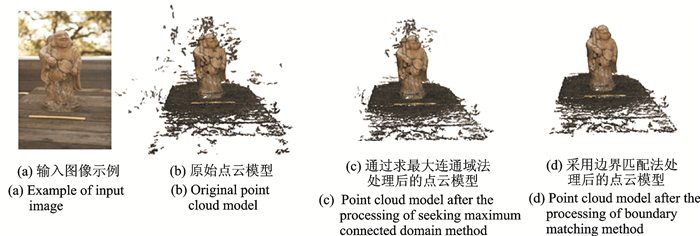
图 2显示了Buddha模型离群点的检测过程。从图 2(b)可以看出,点云中包含大量的离群点;经过求最大连通域法处理后,距离模型主体较远距离的离群点被滤除(见图 2(c)); 而采用边界匹配法处理后,在保留较小有效点簇的同时,模型周围的离群点被滤除(见图 2(d))。
|
图 2 边界匹配法离群点检测 Fig. 2 Outlier detection by using boundary matching method |
3 与模型表面相连的离群点剔除
对于重建点云模型,除上述距离模型主体较远的和模型周围的离群点之外,还包含其他分布状态的离群点。如图 2中Buddha模型底座部分,以及图 3所示紫色数据点。这些离群点要么与模型表面直接相连,要么附着在模型表面,通过空间距离无法有效识别。同时,它们往往具有和模型表面点云相似的密度大小,通过基于密度的方法也无法进行滤除。庆幸的是,这些离群点的产生原因与已识别的离群点一样,都是因为建模对象所处背景的干扰,因此可以采用基于颜色聚类分析的方法来检测。
|
图 3 与模型表面相连的离群点 Fig. 3 Outliers associated with the model surface |
3.1 K-means算法
K-means算法是最为经典的基于划分的聚类方法,其基本思想为:在样本空间中随机选取k个点作为初始聚类中心,然后将剩下的点分别与聚类中心进行比较,将其划分到相似度最高的类中,并采用均值法重新计算该类的聚类中心。迭代上述过程,直至所有点都划分到这k个类中。传统K-means算法存在较为明显的缺陷:(1)需要事先人为设定聚类数目k,这在样本空间未知的情况下,很难精确估算;(2)随机选取初始聚类中心,初始聚类中心的选取会在一定程度上影响最后的聚类结果。
为解决K-means算法的缺陷问题,本文提出了一种改进的K-means方法:首先计算样本空间的局部最大密度区域,将最大密度区域的质心作为初始聚类中心,从而实现自动确定初始聚类数目和位置,避免人为原因造成的误差。
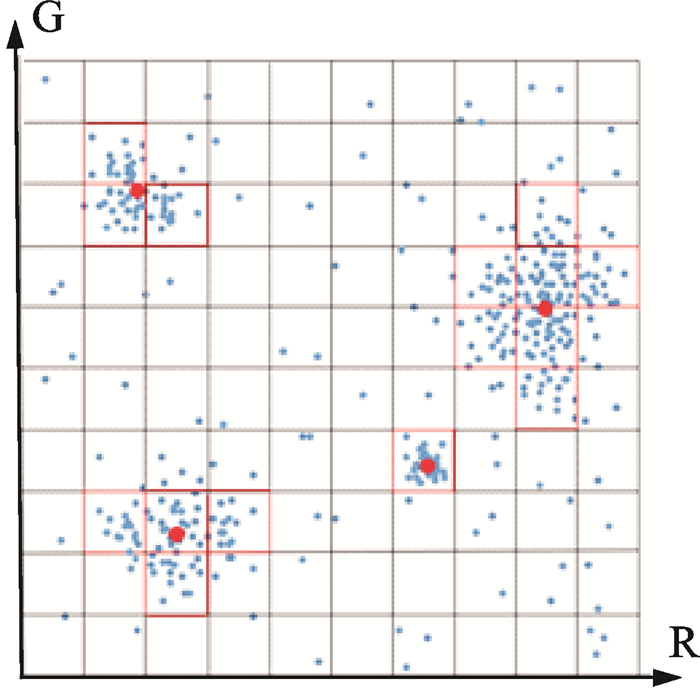
3.2 初始聚类中心选取求局部最大密度是选取初始聚类中心的关键。局部最大密度区域的选取原则为:(1)该区域比周围区域密度大;(2)该区域密度大于ρ。在搜索最大密度区域时,采用划分单元格求连通域的思想。首先根据数据点R,G和B颜色值构建三维空间,以R,G和B为3个坐标轴方向,构造立方体最小包围盒;然后用单元格法对该数据空间进行划分,最后求出每个连通域(连通域中每个单元格包含的数据点密度需大于ρ),将每个连通域当做是一个局部区域。以二维空间为例,如图 4所示,红色方框代表连通域即局部密度最大区域。在这些区域中,每个单元格内密度均大于ρ,ρ=N/p_cell_num,其中N为点云中数据点总个数,p_cell_num为非空单元格数量。
|
图 4 局部最大密度区域 Fig. 4 Local maximum density region |
根据局部最大密度区域法划分可得到聚类数目k,然后,将数据点当做等质量的物理粒子,分别计算每个局部最大密度区域的质心,距离质心最近的数据点视为初始聚类中心,从而得到k个初始聚类中心。在本文的两组试验中,Flowerpot模型的聚类数目为21个,Buddha模型由于模型颜色与背景颜色相似,聚类数目仅为3个。
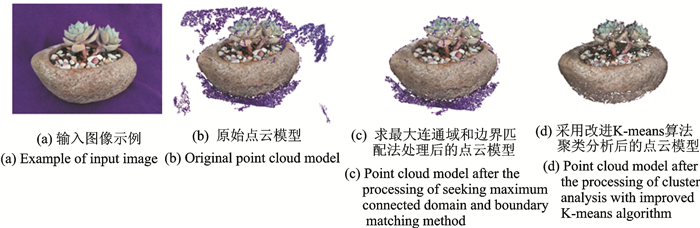
3.3 基于聚类分析的离群点检测首先通过求最大连通域法和边界匹配法检测点云模型中远离模型主体以及模型周围的离群点,并对这些离群点进行标记。然后采用改进K-means方法,在R,G和B颜色值空间对所有数据点进行聚类分析。在每个聚类结果中,如果该类中已经识别的离群点数量所占比例大于δ,那么认定该簇内所有点均为离群点;如果该簇内离群点所占比例小于δ,那么滤除已识别的离群点,只保留非离群点。如图 5所示,对Flowerpot模型进行离群点检测(本实验中δ值取0.3)。通过该方法,与模型表面相连的紫色离群点被成功检测和滤除。
|
图 5 基于聚类分析的离群点检测 Fig. 5 Outlier detection based on clustering analysis |
4 算法实例与分析
对于基于图像重建的三维点云模型,为验证本文所提算法的有效性,针对该离群点检测算法进行了仿真实验。实验所用设备为主频3.4 GHz、内存4.0 GB、Windows 7和64位操作系统的戴尔PC机。
4.1 算法比较首先输入一组以花盆为对象的多角度图像,得到重建三维点云模型Flowerpot如图 5(b)所示。针对该模型,分别采用KNN近邻、区域增长法等5种不同的算法对其进行离群点检测实验。其中,KNN算法通过比较每个数据点与其第k个最近点之间的距离来判断该点是否为离群点;区域增长(Region growth,RG)算法[2]基于距离将点云中所有数据点划分为大小不同的点簇,认定最大的簇为模型表面数据点形成的有效点簇,其他较小簇为离群点簇;表面传播(Surface propagation,SP)算法[8]认定模型表面有效数据点能够形成平滑面片,通过平滑面片传播将有效数据点连接在一起;基于密度(Based on density,BD)算法[6]根据该点邻域内包含的数据点个数来判断它是否为离群点;最后是本文提出的算法。
5种算法在Flowerpot模型和Buddha模型上的离群点检测效果分别如图 6,7所示,执行时间和离群点检测率如表 1,2所示。根据实验结果可以看出,KNN和BD算法能够滤除稀疏离群点,但对于密集聚集的离群点簇无效,当模型表面存在数据点稀疏部分时,这些稀疏点会被视为离群点而滤除。RG和SP的方法会将与模型表面主体分离的有效点簇错误地滤除,而且,SP法还会错误剔除几何形状复杂的模型,如图 6中的花瓣部分数据点。本文算法对于多种分布状态的离群点均有较好的检测效果,并且在运算速度上有较大提升。由于Buddha模型表面数据点的颜色与离群点的颜色非常相近,所以很难通过基于颜色聚类的方法去除底座。

|
图 6 各算法在Flowerpot模型上的离群点检测效果比较 Fig. 6 Outlier detection effect comparison of different algorithms on Flowerpot model |

|
图 7 各算法在Buddha模型上的离群点检测效果比较 Fig. 7 Outlier detection effect comparison of different algorithms on Buddha model |
| 表 1 5种算法在Flowerpot模型上执行时间的对比 Tab. 1 Execution time comparison of five algorithms on Flowerpot model |
| 表 2 5种算法在Buddha模型上执行时间的对比 Tab. 2 Execution time comparison of five algorithms on Buddha model |
4.2 执行时间与效果
采用本文算法分别对3组模型进行离群点检测,在经过求最大连通域、边界匹配和聚类分析后,将实验结果进行对比。执行每一步骤后点云中剩余数据点的数量对比结果如表 3所示,每一步骤的运算时间对比结果如表 4所示。其中,Buddha模型与底座颜色相似,无法用聚类分析进行有效检测,而Stone模型,模型表面点云由一个整体构成,所以不需要进行边界检测和匹配操作。
| 表 3 离群点滤除 Tab. 3 Outliers removal |
| 表 4 算法执行时间 Tab. 4 Algorithm execution time |
5 结束语
本文针对多种离群点的分布状态,提出了一种综合的离群点检测方法。首先通过求最大连通域法滤除远离模型主体的离群点,然后采用边界匹配法,在保留较小有效点簇的同时,滤除模型周围较小离群点簇,最后通过改进的K-means算法对点云数据进行聚类分析,滤除与模型表面相连离群点。为加快数据点搜索速度,通过划分单元格法构建空间拓扑关系。仿真实验结果表明,本文算法相较于另外4种算法,不仅能够检测多种分布状态离群点,而且运算速度更快。但同样存在以下不足:首先,对于与模型表面相连的离群点,如果它们与有效数据点颜色相似,将很难通过颜色聚类方法对其进行检测和滤除,如Buddha模型中的底座部分;其次,需要根据不同的模型人为设定判断点簇是否为离群点簇的比例阈值δ,降低了算法的普适性。这些不足将是以后的研究重点。
| [1] |
Teutsch C. A parallel point cloud clustering algorithm for subset segmentation and outlier detection[J]. Proc Spie, 2011, 8085(17): 1-714. |
| [2] |
Sotoodeh S. Hierarchical clustered outlier detection in laser scanner point clouds[J]. Laser, 2007(1): 383. |
| [3] |
Joachims T. Text categorization with support vector machines: Learning with many relevant features[C]//The 10th European Conferenece on Machine Learning. Chemnitz, Germany: Springer, 1998, 1398(6): 137-142.
|
| [4] |
张毅, 刘旭敏, 隋颖, 等. 基于K-近邻点云去噪算法的研究与改进[J]. 计算机应用, 2009, 29(4): 1011-1014. Zhang Yi, Liu Xumin, Sui Ying, et al. Research and improvement of denoising method based on K-neighbors[J]. Journal of Computer Applications, 2009, 29(4): 1011-1014. |
| [5] |
Rusu R B, Marton Z C, Blodow N, et al. Towards 3D point cloud based object maps for household environments[J]. Robotics & Autonomous Systems, 2008, 56(11): 927-941. |
| [6] |
Weyrich T, Pauly M, Keiser R, et al. Post-processing of scanned 3D surface data[C]//Eurographics Conference on Point-based Graphics. Switzerland: Eurographics Association Aire-la-Ville, 2004: 85-94.
|
| [7] |
Ma M X, Ngan H Y T, Liu W. Density-based outlier detection by local outlier factor on large scale traffic data[J]. Electronic Imaging, 2016(2): 385. |
| [8] |
Shen J, Yoon D, Shehu D, et al. Spectral moving removal of non-isolated surface outlier clusters[J]. Computer-Aided Design, 2009, 41(4): 256-267. DOI:10.1016/j.cad.2008.09.003 |
| [9] |
Jung J, Hong S, Yoon S, et al. Automated 3D wireframe modeling of indoor structures from point clouds using constrained least-squares adjustment for as-built BIM[J]. Journal of Computing in Civil Engineering, 2015, 30(4): 0401-5074. |
| [10] |
Diwakar M, Kumar M. CT image noise reduction based on adaptive wiener filtering with wavelet packet thresholding[C]//International Conference on Parallel, Distributed and Grid Computing.Solan, India: IEEE, 2015: 94-98.
|
| [11] |
Mazhari M, Hasanzadeh R P R. Suppression of noise in SEM images using weighted local hysteresis smoothing filter[J]. Scanning, 2016, 38(6): 634-643. DOI:10.1002/sca.v38.6 |
| [12] |
Colding T, Minicozzi W I, Pedersen E. Mean curvature flow[J]. Bulletin of the American Mathematical Society, 2015, 52(9): 4551-4587. |
| [13] |
Fleishman S, Drori I, Cohen-Or D. Bilateral mesh denoising[J]. ACM Transactions on Graphics, 2003, 22(3): 950-953. DOI:10.1145/882262 |
| [14] |
Jones T R, Durand Desbrun M. Non-iterative, feature-preserving mesh smoothing[J]. ACM Transactions on Graphics, 2003, 22(3): 943-949. DOI:10.1145/882262 |
| [15] |
Alexa M, Behr J, Cohen-Or D, et al. Point set surfaces[C]//Proceedings of the IEEE Conference on Visualization.[S.l.]: IEEE, 2001, 22(4): 21-28.
|
| [16] |
Fleishman S, Cohen-Or D, Silva, et al. Robust moving least-squares fitting with sharp features[J]. ACM Transactions on Graphics, 2005, 24(3): 544-552. DOI:10.1145/1073204 |
| [17] |
Oztireli A. C, Guennebaud G, Gross M. Feature preserving point set surfaces based on non-linear kernel regression[J]. Computer Graphics Forum, 2009, 28(2): 493-501. |
| [18] |
Mederos B, Velho L, De Figueiredo L H. Robust smoothing of noisy point clouds[C]//Proc SIAM Conference on Geometric Design & Computing. Brentwood, TN: Nashboro Press, 2003: 405-416.
|
| [19] |
Wang Y, Feng H Y. Outlier detection for scanned point clouds using majority voting[J]. Computer-Aided Design, 2015, 62(C): 31-43. |
 2018, Vol. 33
2018, Vol. 33


