2. 安徽大学计算机智能与信号处理教育部重点实验室, 合肥, 230601
2. Key Laboratory of Intelligent Computing and Signal Processing of Ministry of Education, Anhui University, Hefei, 230601, China
随着互联网的发展,各种复杂网络如雨后春笋般出现,链路预测作为数据挖掘领域的研究方向之一,得到越来越多的关注。链路预测是指如何通过已知的网络节点以及网络结构等信息,预测网络中尚未产生连边的两个节点之间产生链接的可能性[1-3]。这种预测既包含了对未知链接的预测,也包含了对未来链接的预测。链路预测对一些实际问题具有重要的理论研究意义,如网络的动态演化等。刘宏鲲等利用链路预测的方法推断出影响航空网络演化的重要因素[4]。链路预测也具有广泛的实际应用价值,如电子商务网站向用户推荐感兴趣的商品,在线社交网络中的好友推荐[5];在蛋白质相互作用网络中,利用链路预测算法预测尚未发现的蛋白质分子之间的相互作用关系,有助于加快揭开蛋白质网络的真实面目[6, 7];在科学家合作网络中识别科学家之间潜在的合作可能[8];此外链路预测方法在识别犯罪网络、检测和发现恐怖袭击等社会安全领域也能发挥重要作用。
1 链路预测研究现状链路预测早期的研究方法主要是基于马尔科夫链和机器学习。文献[9]应用马尔科夫链进行网络的链路预测与路径分析。之后文献[10]将基于马尔科夫链的预测方法扩展到自适应网站的预测中。通过提取网络的特征,机器学习方法通过训练模型来进行链路预测。O′Madadhain等应用了几种分类器来预测网络中的潜在链接[11]。以上的两种方法比较复杂,从复杂网络的角度进行链路预测研究是一种新的方式,这种方法较简单,且具有普适性。基于拓扑相似性的链路预测算法是近几年的主流方法,这种方法的一个重要假设就是两个节点越相似,则节点间存在链接的可能性越大,因此该方法的的一个关键问题就是如何来定义节点之间的相似性[12]。
通常可以将拓扑网络中的各种信息融合在一起来定义节点之间的相似性,其中最重要的信息是节点属性和网络结构,节点属性信息有较高的预测精度,但是收集这些信息不易。即使可以获得节点属性信息,从这些复杂的信息中鉴别出哪些信息对预测有用也是一件困难的事。与节点属性信息相比较,网络结构信息更容易获取。并且,基于网络结构信息的链路预测方法对结构相似的网络具有普遍适用性。因此,近些年来基于网络结构相似性链路预测方法受到越来越多的关注。
基于局部信息、基于路径和基于随机游走的相似性算法是最主要的3种基于结构相似性的链路预测方法。共同邻居指标(Common neighbors, CN)[13]是最简单的基于局部信息的相似性指标,该指标认为两节点的相似度正比于共同邻居节点数量。与CN相似的Jaccard算法[14]就是CN算法中计算节点相似性的归一化形式。如果考虑共同邻居节点的度,著名的有Admic-Adar指标(AA)[15]。受到网络中资源分配过程的启发,周涛等提出了资源分配指标(Resource allocation, RA)[16]。基于路径的相似性指标有局部路径指标(Local path, LP)[16, 17],它只考虑了二阶路径数目。Katz指标[18]考虑了网络的所有路径。有相当数量的相似性指标基于随机游走过程定义,包括平均通勤时间(Average commute time, ACT)[19], 余弦相似性指标cos+[20],有重启的随机游走指标(Random walk with restart, RWR)[21]以及基于局部游走的LRW(Local random walk)和SRW(Superposed random walk)指标[22]。以上的链路预测方法除了Katz指标[18],其他的都是基于局部的相似性指标。这种指标由于其复杂度较低,得到了广泛的应用。
随着链路预测得到越来越多的关注,近年来各种新颖的链路预测方法相继被提出。文献[23]根据网络中路径上潜在的资源传播的思想,提出一种扩展的RA算法。文献[24]的目的是利用社团结构信息来提高基本的链路预测方法的性能。该信息来自于同一个社团内的两个节点所处的社团层次数目(利用了分层的社团发现算法)。结果显示有价值的社团信息可以提高链路预测的效果。但是无论是经典方法,还是最新方法,很多都忽略了每个节点的贡献度不同以及共同邻居节点之间的链接紧密度信息。因此,本文提出一种新的链路预测算法,综合考虑每个共同邻居节点的差异性以及链接的紧密度。
2 问题描述及预测方法 2.1 问题描述定义一个无向无权网络G(V, E),其中V代表节点的集合,E为边的集合。网络的节点总数为N,边的数量为M,所有的节点对组成全集U。这样,链路预测问题可描述为:定义某种相似性指标,对没有连边的节点对(x, y),计算其相似度Sxy,Sxy越大,则节点对(x, y)出现连边的可能性越大。
为了测试算法精度,将集合E分为训练集ET和测试集EP。将属于全集U但不属于集合E的边称为不存在的边,属于U但不属于训练集ET的边称为未知边。在本文中,训练集所占比例为90%,测试集为10%。
2.2 链路预测方法基于局部信息的相似性算法由于其计算复杂度低,适合规模较大的复杂网络,故得到广泛使用。在本文中,将会和CN,AA,RA和Jaccard这4种经典的相似性算法以及基于节点连接密度的算法CNBIDE进行比较。本文使用的符号说明如表 1所示。
| 表 1 符号说明 Tab. 1 Symbolic representation |
CN算法[13]。该算法中,两个节点x和y的相似性就定义为它们共同邻居的数量,即
| $ \mathit{\boldsymbol{S}}_{xy}^{{\rm{CN}}} = \left| {\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} \right| $ | (1) |
Jaccard算法[13]。Jaccard指标代表了一个随机选择的节点x或y的邻居是x和y的共同邻居的可能性,即
| $ \mathit{\boldsymbol{S}}_{xy}^{{\rm{Jaccard}}} = \frac{{\left| {\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} \right|}}{{\left| {\mathit{\Gamma }\left( x \right) \cup \mathit{\Gamma }\left( y \right)} \right|}} $ | (2) |
AA算法[15]。该算法认为度小的共同邻居节点对连边影响更大, 即
| $ \mathit{\boldsymbol{S}}_{xy}^{{\rm{AA}}} = \sum\limits_{z \subset \mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} {\frac{1}{{\log {k_z}}}} $ | (3) |
RA算法[16]。受网络资源分配过程的启发,周涛等提出了AA算法。该算法惩罚了度大的共同邻居节点,即
| $ \mathit{\boldsymbol{S}}_{xy}^{{\rm{RA}}} = \sum\limits_{z \subset \mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} {\frac{1}{{{k_z}}}} $ | (4) |
CNBIDE算法[25]。该算法考虑了共同邻居的链接紧密度,然后和CN算法相结合,即
| $ \mathit{\boldsymbol{S}}_{xy}^{{\rm{CNBIDE}}} = \left| {\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} \right| * \left( {1 + \frac{{\left| Z \right|}}{{\frac{1}{2}\left| {\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} \right|\left( {\left| {\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} \right| - 1} \right)}}} \right) $ | (5) |
式中Z={(a, b)|(a, b)∈E,a∈Γ(x)∩Γ(y),b∈Γ(x) ∩Γ(y)}。
这几种链路预测算法都是从共同邻居节点的角度提出。CN算法只考虑了共同邻居的数量,未对它们的重要性做任何区分。Jaccard考虑了除共同邻居之外的其他邻居节点,但也只是考虑到了邻居节点的数量对链接产生的影响。AA和RA算法比较相似,区别在于定义共同邻居节点权重的方式,前者以1/logk的形式递减,后者以1/k的形式递减。CNBIDE算法考虑了共同邻居数量,也考虑了共同邻居之间的链接密度。然而,这几种算法并未考虑到每个共同邻居节点对连边的贡献度是不同的,即不能简单地将邻居节点同等对待。本文针对以上问题提出一个新的节点相似性算法,既考虑了共同邻居的链接紧密度,也考虑了共同邻居节点的贡献度。
3 结合共同邻居贡献度和连接紧密度的链路预测方法 3.1 共同邻居节点的链接紧密度在基于节点相似性的链路预测算法中,计算节点间的连边概率通常是基于它们的共同邻居节点信息。但是,在以往的算法中,利用的大多是共同邻居的数量信息或者度信息,忽略了共同邻居之间的相互关系,而共同邻居之间的链接关系往往对连边有极大的影响。
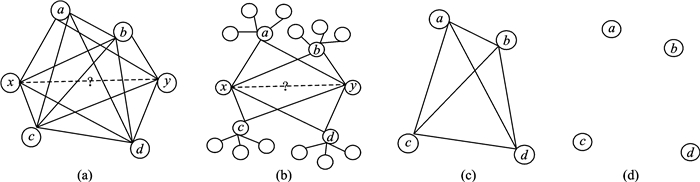
图 1表示2个简单的网络拓扑结构图及抽取的x和y节点共同邻居的拓扑结构。目的是通过图 1,分析节点x和y之间存在链接的概率大小。图 1中(a),(b)两个网络拓扑图中,节点x和y的共同邻居节点都是4个,都是a, b, c, d, 且两图中的a, b, c, d节点的度值均相等。如果利用基于共同邻居的链路预测算法来进行预测(如CN等),则两图中x和y节点的相似性概率相同。如果利用基于共同邻居的度信息的链路预测算法(如AA,RA等)进行预测,两图中x和y节点之间存在链接的概率也相等。图 1中(c),(d)分别是由(a),(b)中节点x和y的共同邻居节点a, b, c, d及它们之间的连边组成的子网络。通过比较(c)和(d), 可以看出图(c)中节点之间两两互连,而图(d)的各个节点之间并无关联。假设节点x和y代表现实中的两个人,他们都有a, b, c, d 4个相同的朋友,但是一种情况是这4个共同朋友都认识,彼此是朋友关系,可以理解为都在同一个单位或者有共同的爱好,在这种情况下,x和y通过共同朋友结识或者产生联系的概率大大增大。而如果共同朋友没有任何交集,彼此孤立存在,则x和y认识的机会则大为降低。
|
图 1 x,y节点及其共同邻居组成的小网络 Fig. 1 Small network composed of x, y nodes and their neighbors |
考虑到共同邻居的链接紧密程度对最终的链接产生的影响,本文引入了链接紧密度的概念。如果共同邻居节点之间有更多的连边,也就是链接更紧密,则认为被预测节点之间存在链接的概率更高。本文定义一个表示邻居节点集合中各节点链接紧密程度的指标—链接紧密度,具体定义如下
| $ LD\left( {x,y} \right) = \left\{ \begin{array}{l} 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right) \in \emptyset \\ \frac{{\left| Z \right|}}{{\left| {\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} \right|}}\;\;\;\;\;\;\mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right) \notin \emptyset \end{array} \right. $ | (6) |
式中Z={(a, b)|(a, b)∈E,a∈Γ(x)∩Γ(y),b∈Γ(x)∩Γ(y)},Γ(x)∩Γ(y)表示节点x和y的共同邻居节点集合。
3.2 节点贡献度基于相似性的的链路预测方法大都仅考虑共同邻居节点的数量或度值信息来评估节点间连边的概率。这些方法将每个共同邻居节点都看成是没有差别的,但是在实际的网络中,不同节点的影响力是不同的。例如在社交网络中,外向的人往往要比内向的人引导两个人相识的作用更强。因此,如果对每个共同邻居节点的差异性不加以区分,将它们对节点连边的贡献度看成是相同的,可能对链路预测的准确性产生影响。
在社交网络中,两个节点如果都和同一个节点相链接,把两节点间的节点称为两节点的共同邻居节点,不同的共同邻居节点对节点连边的贡献度是不同的,本文把节点耦合聚簇系数[26]看成每个共同邻居节点对连边产生的贡献度。该指标综合了每个节点的度信息和聚簇系数信息,体现了每个节点的差异性。
节点贡献度公式为
| $ NC\left( n \right) = \frac{{\sum\limits_{i \in {C_n}} {\left( {\frac{1}{{{k_i}}} + C\left( i \right)} \right)} }}{{\sum\limits_{j \in {\mathit{\Gamma }_n}} {\left( {\frac{1}{{{k_j}}} + C\left( j \right)} \right)} }} $ | (7) |
式中Γ(n)是节点n的邻居节点集合。如果(M, N)代表待预测的节点对,则n∈Γ(M)∩Γ(N)。Cn表示节点n的邻居节点和待预测节点M,N的邻居节点的交集再加上M和N节点所组成的集合,也即是Cn=Γ(M)∩Γ(N)∩Γ(n)∪{M, N}。
C(n)表示节点n的聚簇系数,其计算公式为
| $ C\left( n \right) = \frac{{2 \times {E_n}}}{{{k_n} \times \left( {{k_n} - 1} \right)}} $ | (8) |
式中En表示节点n的邻居节点之间的链接数目。kn表示节点n的度值。
在式(2)中,因为Cn⊆Γ(n),则有
传统的链路预测方法大多考虑的网络结构较少,有的只考虑共同邻居个数和度信息,有的只考虑了路径的数量。如果考虑更多的网络结构信息,对预测的准确率可能会有一个提升。基于此,本文从待预测节点的共同邻居节点出发,既考虑了每个节点的差异性,用节点耦合聚簇系数来表示每个共同邻居节点对待预测节点产生连边的贡献度。同时,共同邻居节点之间的紧密程度也可以用来衡量待预测节点之间的相似程度。如果共同邻居节点之间链接越紧密,说明待预测节点之间有更多的相似性性质,相似性程度越高。
将节点贡献度和链接紧密度相结合,本文提出了结合共同邻居贡献度和连接紧密度的链路预测(Node contribution and link density of the common neighbor nodes, LDNC)算法。LDNC算法中节点x和y的相似度矩阵Sxy定义为
| $ {\mathit{\boldsymbol{S}}_{xy}} = \frac{1}{{1 + {{\rm{e}}^{ - LD\left( {x,y} \right)}}}} + \sum\limits_{z \in \mathit{\Gamma }\left( x \right) \cap \mathit{\Gamma }\left( y \right)} {NC\left( z \right)} $ | (9) |
式中: LD(x; y)是x, y节点的共同邻居之间的链接紧密度; NC(z)表示x; y节点的共同邻居节点z对x, y节点连边的贡献度。由于网络中连边密度的差异,节点之间的链接紧密度差异较大,经反复实验,将节点的链接紧密度进行归一化后,预测精确度最高。
LDNC算法的具体过程如下:
输入:无向无权网络Network
输出:评价指标结果(AUC,Precision)
开始:
(1) 统计网络中被预测节点对(x, y)的共同邻居个数以及它们之间的连边个数,使用式(6)得出节点对(x, y)的共同邻居节点连边紧密度。
(2) 使用式(7)得出被预测节点对(x, y)的每个共同邻居节点对其产生连边的贡献度。
(3) 根据式(9)计算被预测节点对(x, y)之间的相似度Sxy。最后求得相似度矩阵SIM。
(4) 根据相似度矩阵SIM计算评价指标(AUC,Precision)的结果。
结束
3.4 算法复杂度分析链路预测算法一般分为基于局部信息和基于全局信息。前者的优势在于时间复杂度较低,适合大规模的网络应用,而后者的时间复杂度则较高。基于局部信息的最简单的链路预测算法是CN算法[13],它的时间复杂度为O(n2)。Katz算法[18]是一种代表性的基于全局信息的链路预测算法,它的时间复杂度为O(n3)。而本文提出的LDNC算法的时间复杂度为O(n2), 和CN算法相同,可适用于大规模网络。
4 实验结果与分析 4.1 评价指标链路预测的评价指标主要有AUC(Area under the receiver operating characteristic curve)、精确度(Precision)。AUC是比较常用的一种评价指标,它是从整体上衡量算法的精确度[27]。Precisi on只考虑排在前L位的边是否预测准确[28]。
AUC指标[27]。AUC可以理解为在测试集中边的分数值比随机选择的一个不存在边的分数值高的概率,也就是说,每次随机从测试集中选取一条边与随机选择的不存在的边进行比较,如果测试集中的边的分数值大于不存在边的分数值,就加1分;如果两个分数值相等,就加0.5分。这样独立地比较n次,如果n′次测试集中的边的分数值大于不存在的边的分数,n″次两个分数值相等,则AUC定义为
| $ {\rm{AUC}} = \frac{{n' + 0.5n''}}{n} $ | (10) |
若所有分数都随机产生,则AUC=0.5。因此,AUC大于0.5的程度衡量了算法比随机算法准确的程度。
Precision指标[28]。Precision指标定义为在前L个预测连边中被预测准确的比例。如果有m个预测准确,即排在前L的连边中有m个在测试集中,则Precision定义为
| $ {\rm{Precision}} = m/L $ | (11) |
Precision值的大小与参数L有关,对于给定的L,Precision值越大,则预测结果越准确。
4.2 实验数据集实验时,在保证网络连通的情况下,将网络中的连边随机的划分为训练集和测试集,其中训练集占90%,测试集占10%。为了验证LDNC算法是否有效,实验时选取了9个涵盖不同领域的真实网络数据集,分别是:
(1) 食物链网络1(FWMW)[29]
这是红树林河口湿季的食物链网络,包含97个节点和1 492条边,其中节点表示生物,边表示生物之间的捕食关系。本文将该网络进行无向处理。
(2) 食物链网络2(FWFW)[30]
这是佛罗里达海湾雨季的食物链网络。包含128种节点和2 075条边, 其中节点表示生物,边表示生物之间的捕食关系。本文将该网络进行无向处理。
(3) 爵士音乐家合作网络(Jazz)[31]
这是一个爵士音乐家合作网络,包含198个节点和2 742条边,其中音乐家用节点表示,节点间的连边表示两个音乐家是朋友关系。
(4) 线虫的神经网络(C.elegans)[32]
这是秀丽隐杆菌(C.elegans)的神经网络,包含了297个节点和2 345条边, 其中神经元用节点来表示,边代表神经元突触或者间隙连接。本文将该网络进行无向处理。
(5) 美国航空网络(USAir)[33]
这是美国航空网络,有332个节点和2 126条边, 其中机场用边表示,连边表示航线。如果两个机场有直飞航线,则机场所对应的两个节点之间有一条连边。
(6) 美国政治博客网络(PB)[34]
这是一个由博客网页之间的链接关系组成的网络,包含1 490个节点和19 090条有向边,其中节点为博客网页,边表示网页之间的超链接。本文将该网络进行无向处理。
(7) 科学家合作网络(NS)[35]
这个一个科学家合著网络,包含了1 589个节点和2 742条边,其中节点代表科学家,边代表科学家之间的合作关系。
(8) 蛋白质相互作用网络(Yeast)[36]
节点表示蛋白质,边表示其相互作用关系。包含2 375个节点和11 693条边。
(9) 电力网络(Power)[32]
这是美国西部电力网络,包含4 941个节点和6 594条边。其中节点代表变电站或换流站,连边表示它们之间的高压线。
表 2列出刻画网络特征常用的统计量符号及其含义,表 3列出9个真实网络数据集的统计量信息。
| 表 2 统计量符号及其含义 Tab. 2 Statistical symbols and meaning |
| 表 3 9个真实网络的统计量 Tab. 3 Statistical measure of nine real networks |
4.3 实验结果分析
本文采用AUC和Precision作为衡量链路预测算法准确性的指标。LDNC算法和CN, AA, RA, Jaccard和CNBIDE算法的比较结果如表 4和表 5所示。表 4是AUC指标的结果,表 5是Precision指标(L=100)的结果,加黑字体表示最优结果。图 2给出了6种算法的Precision值随L值变化的结果。
| 表 4 评价指标AUC的结果 Tab. 4 The results of AUC on 9 real-networks |
| 表 5 评价指标Precision的结果(L=100) Tab. 5 The result of precision on 9 real-networks (L=100) |
|
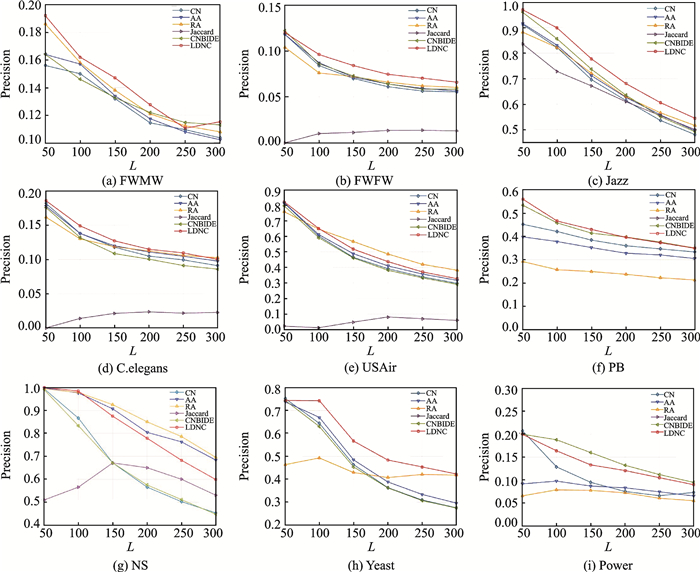
图 2 精确度Precision与L的关系 Fig. 2 Relationship between Precision and L |
观察表 4 AUC指标的结果,在FWMW,FWFW,USAir,NS,Yeast和Power这6个网络上,LDNC算法均取得了最优值,而在C.elegans网络上,LDNC和RA的AUC值相同,也是最优。从表 4也可以看出,除了LDNC算法,RA算法在各个数据集上表现得最好,这说明网络中节点度对预测结果的影响是巨大的。而当网络的平均度较大时,RA指标表现最好。Jazz和PB这两个网络的平均度较大,在AUC评价指标上也好于LDNC, 但是用Precision指标进行比较,LDNC预测准确性好于RA。
观察表 5 Precision指标的结果,在FWMW,FWFW,Jazz,C.elegans,USAir,PB,NS和Yea st这8个网络中,LDNC算法的预测准确率最高。其中在NS和Yeast网络中,预测精度提升超过了10%。在Power网络中CNBIDE取得了最优的预测精度,但LDNC算法的预测精度也超过了4种经典算法。Precison定义为前L个预测边中预测准确的比例,是一种局部评价指标。而LDNC算法在Precision上表现较好,说明LDNC算法对排名靠前的边预测准确率高。
实验结果表明,和CN,AA,RA和Jaccard 4种传统链路预测算法相比,LDNC算法预测准确性更高,具有较好的预测效果。同时和基于链接紧密度的链路预测算法CNBIDE算法相比,也取得了更优的预测效果,说明不同的邻居节点对节点连边的贡献度是不同的,LDNC算法考虑了这种差异性,取得了更好的效果。另外,由于Precision评价指标的最终结果和L的取值有关,在图 2中列出了LDNC算法和CN,AA,RA,Jaccard和CNBID E算法的Precision值随L值变化的情况。其中L的取值范围是[50, 300],间隔是50。结果表明,随着L值的增加,各个算法的Precision值总体呈下降趋势,但是LDNC算法总体上是最优的。
5 结束语本文提出了一种新的链路预测算法,为一种结合共同邻居贡献度的节点相似性链路预测算法。该算法既考虑了共同邻居节点的差异性,用节点耦合聚簇系数来定义每个节点对连边产生的贡献度,又考虑了共同邻居之间的连边情况,用连边的紧密程度来衡量待预测节点之间的相似程度。与4种传统的预测算法和基于节点紧密度的算法CNBI DE在9组真实网络数据集上进行实验,结果表明,LDNC算法具有更高的预测准确度。今后的研究主要从两方面进行。首先,可以考虑更多的节点边信息,不仅要考虑连边数量,也要考虑路径信息。其次,社团也是网络的一个重要结构,如果两节点在同一社团内,它们之间的相似性程度则相对较高,则它们之间的连边概率则相对较大,因此如何将社团信息与其他的网络信息相结合,也是未来的一个研究方向。
| [1] |
Lü L, Zhou T. Link prediction in complex networks:A survey[J]. Physica A Statistical Mechanics & Its Applications, 2011, 390(6): 1150-1170. |
| [2] |
吕琳媛. 复杂网络链路预测[J]. 电子科技大学学报, 2010, 39(5): 651-661. Lü Linyuan. Link prediction on complex networks[J]. Journal of University of Electronic Science and Tech nology of China, 2010, 39(5): 651-661. DOI:10.3969/j.issn.1001-0548.2010.05.002 |
| [3] |
Getoor L, Diehl C P. Link mining:A survey[J]. ACM Sigkdd Explorations Newsletter, 2005, 7(2): 3-12. DOI:10.1145/1117454 |
| [4] |
刘宏鲲, 吕琳媛, 周涛. 利用链路预测推断网络演化机制[J]. 中国科学:物理学力学天文学, 2011, 41: 816-823. Liu Hongkun, Lü Linyuan, Zhou Tao. Uncovering the network evolution mechanism by link prediction[J]. Sci Sin Phys Mech Astron, 2011, 41: 816-823. |
| [5] |
Aiello L M, Barrat A, Schifanella R, et al. Friendship prediction and homophily in social media[J]. ACM Transactions on the Web, 2012, 6(2): 1-33. |
| [6] |
Yu H, Braun P, Yildirim M A, et al. High-quality binary protein interaction map of the yeast interactome network[J]. Science, 2008, 322(5898): 104-110. DOI:10.1126/science.1158684 |
| [7] |
Stumpf M P H, Thorne T, Silva E D, et al. Estimating the size of human interactome[J]. Proceedings of the National Academy of Sciences, 2008, 105(19): 6959-6964. DOI:10.1073/pnas.0708078105 |
| [8] |
Gu Q, Zhou J, Ding C H Q. Collaborative filtering: Weighted nonnegative matrix factorization incorporating user and item graphs[C]//SIAM International Conference on Data Mining.Columbus, Ohio, USA: [s.n.], 2010: 199-210.
|
| [9] |
Sarukkai R R. Link prediction and path analysis using Markov chains[J]. Computer Networks, 2000, 33(1-6): 377-386. DOI:10.1016/S1389-1286(00)00044-X |
| [10] |
Zhu J, Hong J, Hughes J G. Using markov chains for link prediction in adaptive web sites[J]. Lecture Notes in Computer Science, 2004, 2311: 60-73. |
| [11] |
Lü Linyuan. Research status and prospect of link predict ion[EB/OL]. http://blog.sciencenet.cn/home.php?mod=space&uid=329471&do=blog&id=318268,2010-04-30.
|
| [12] |
Lorrain F, White H C. Structural equivalence of in dividuals in social networks[J]. Journal of Mathematical Sociology, 1971, 1(1): 49-80. DOI:10.1080/0022250X.1971.9989788 |
| [13] |
Jaccard P. Etude de la distribution florale dans une portion des Alpes et du Jura[J]. Bulletin De La Societe Vaudoise Des Sciences Naturelles, 1901, 37(142): 547-579. |
| [14] |
O'Madadhain J, Hutchins J, Smyth P. Prediction and ranking algorithms for event-based network data[J]. A CM Sig kdd Explorations Newsletter, 2005, 7(2): 23-30. DOI:10.1145/1117454 |
| [15] |
Adamic L A, Adar E. Friends and neighbors on the Web[J]. Social Networks, 2003, 25(3): 211-230. DOI:10.1016/S0378-8733(03)00009-1 |
| [16] |
Zhou T, Lü L, Zhang Y C. Predicting missing links via local information[J]. The European Physical Journal B, 2009, 71(4): 623-630. DOI:10.1140/epjb/e2009-00335-8 |
| [17] |
Lü L, Jin C H, Zhou T. Similarity index based on local paths for link prediction of complex net works[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2009, 80(2): 593-598. |
| [18] |
Katz L. A new status index derived from sociometric an alysis[J]. Psychometrika, 1953, 18(1): 39-43. DOI:10.1007/BF02289026 |
| [19] |
Klein D J, Randic M. Re sistance distance[J]. Journal of Mathematical Chemistry, 1993, 12(1): 81-95. DOI:10.1007/BF01164627 |
| [20] |
Fouss F, Pirotte A, Renders J M, et al. Random-walk computation of similarities between nodes of a graph with application to collaborative recommendation[J]. IEEE Transactions on Knowledge & Data Engineering, 2007, 19(3): 355-369. |
| [21] |
Brin S, Page L. Reprint of:The anatomy of a large-scale hypertextual web search engine[J]. Computer Networks, 2012, 56(18): 3825-3833. DOI:10.1016/j.comnet.2012.10.007 |
| [22] |
Liu W, Lu L. Link prediction based on local random walk[J]. EPL, 2010, 89(5): 58007-58012. DOI:10.1209/0295-5075/89/58007 |
| [23] |
Liu S, Ji X, Liu C, et al. Extended resource allocation in dex for link prediction of complex network[J]. Physica A Statistical Mechanics & Its Applications, 2017, 479: 174-183. |
| [24] |
Deylami H A, Asadpour M. Link prediction in social networks using hierarchical community detection[C]//Information and Knowledge Technology (IKT), 20157th Conference on.[S.l.]: IEEE, 2015: 1-5.
|
| [25] |
李淑玲.基于相似性的链接预测方法研究[D].哈尔滨: 哈尔滨工程大学, 2012. Li Shuling.Research on link prediction methods based on the similarity[D]. Harbin: Harbin Engineering University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10217-1012517903.htm |
| [26] |
Li F, He J, Huang G, et al. Node-coupling clustering approaches for link prediction[J]. Knowledge-Based Systems, 2015, 89(C): 669-680. |
| [27] |
Hanley J A, Mcneil B J. The meaning and use of the area under a receiver operating characteristic (ROC) curve[J]. Radiology, 1982, 143(1): 29-36. DOI:10.1148/radiology.143.1.7063747 |
| [28] |
Herlocker J L. Evaluating collaborative filtering recommender systems[J]. ACM Transactions on Information Systems, 2004, 22(1): 5-53. |
| [29] |
Baird D, Luczkovich J, Christian R R. Assessment of spatial and temporal variability in ecosystem attributes of the St Marks National Wildlife Refuge, Apalachee Bay, Florida[J]. Estuarine Coastal & Shelf Science, 1998, 47(3): 329-349. |
| [30] |
Ulanowicz R E, Bondavalli C, Egnotovich M S. Network analysis of trophic dynamics in south Florida ecosystem, fy 97: The florida bay ecosystem[EB/OL]. http://www.cbl.umces.edu/~atlss/FBay701.html, 1998.
|
| [31] |
Gleiser P M, Danon L. Community structure in jazz[J]. Advances in Complex Systems, 2003, 6(4): 565-573. DOI:10.1142/S0219525903001067 |
| [32] |
Watts D J, Strogatz S H. Collectivedynamics of 'small-world' net works[J]. Nature, 1998, 440-442. |
| [33] |
Batagelj V, Mrvar A. Pajek-program for large network analysis[J]. Connections, 1998, 21(2): 47-57. |
| [34] |
Adamic L A, Glance N. The political blogosphere and the 2004 US election: Divided they blog[C]//Proceedings of the 3rd International Workshop on Link Discovery. New York: ACM, 2005: 36-43.
|
| [35] |
Newman M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Physical Review E, 2006, 74(3): 036104. DOI:10.1103/PhysRevE.74.036104 |
| [36] |
Von M C, Krause R, Snel B, et al. Comparative assessment of large-scale data sets of protein-protein interactions[J]. Nature, 2002, 417(6887): 399-403. DOI:10.1038/nature750 |
 2018, Vol. 33
2018, Vol. 33

