在日常生活中,很多情景都涉及到评价问题,需要从某些已存在的对象中选择出最符合要求的对象。其中存在如下一种情况:这些待评价的对象数目较大,并且对象间具有一定的层级关系,也就是说某些对象在物理上能映射到一个对象上,比如,某些学生属于同一个班级,班级和学生都是需要评价的对象。在目前已有的评价模型中,如周海平等[1]的工作,还没有能反映当前层次的决策属性的模型。基于这种情况,建立一个能对各级对象做出评价的模型具有重要的意义。
因此,本文针对这种评价对象多、评价对象之间具有层级关系的问题,提出了一种基于逼近理想点排序法(Technique for order performance by similarity to ideal solution,TOPSIS)的三支决策评价模型。本模型在评价前增加了预分类的思想,预分类的结果在一定程度上影响最终的评价结果。考虑到企业的需求,高层决策者往往并不关心对象之间的绝对序关系,而更关注哪些对象比较好、哪些对象比较差等。因此,本文结合三支决策思想,将需要评价的对象分到好、中、差3个类中。
1 相关工作TOPSIS根据有限个评价对象与理想化目标的接近程度进行排序,在现有的对象中进行相对优劣的评价。其基本原理是通过检测评价对象与最优解、最劣解的距离来进行排序,若评价对象最靠近最优解的同时又最远离最劣解,则为最好,否则不为最优。其中最优解的指标值都达到各评价指标的最优值; 最劣解的各指标值都达到评价指标的最差值。
TOPSIS是由Hwang和Yoon[2]在1981年提出,并由Chen和Hwang[3]在1992年完善。大多数研究用该方法来解决供应商选择问题[4]。Büyüközkan和Çifçi[5]在2012年结合模糊集和TOPSIS方法来解决多目标决策问题。随后,结合模糊集的基于层次分析法(Analytic hierarchy process,AHP)和TOPSIS的改进方法被广泛应用在很多决策问题中[6-7]。更多的关于TOPSIS和Fuzzy TOPSIS的讨论请见Madi等[8]的工作。
陆伟锋和唐厚头[9]认为,尽管TOPSIS方法比一般加权求和法更具合理性,但自身也存在一些不足,主要表现在出现逆序和无法绝对排序以及权重的设定不合理等方面。因此,本文提出的方法选用AHP来计算属性的权重以弥补TOPSIS方法的不足。AHP方法因其灵活性和分解决策问题的能力经常被用作权重的计算,它将众多因素构成的复杂系统分不同层次进行评价,利用下层对上层的重要性来计算属性权重。AHP最开始由Wind和Saaty[10]提出,已经在社会科学和管理领域广泛应用,比如项目管理[11]和军事应用等。AHP合并了专家的观点评价权重,并且把复杂的决策系统变为简单基本层次结构系统。评价方法依据比例尺度两两比较属性之间的重要性[12]。
三支决策是现实生活中常用的策略之一,现实世界中的许多场景都面临着决策问题,人们通常使用可信的信息与证据来做出决策。在广泛使用的二支决策(接受或者拒绝)中,通常称之为正决策(正域决策)或者负决策(负域决策)。但是,面对信息不充分、证据不明显的情况,人们往往难以做出正决策或者负决策,这时候一般会选择既不接受、也不拒绝的第三种方案,即延迟决策,或者称之为边界决策(边界域决策)。三支决策就是在传统的二支决策中加入第三种决策。三支决策已经在群决策[13]、垃圾邮件过滤[14]、医疗诊断决策[15]、参数选择[16]和三支决策聚类等[17]诸多领域得到了非常广泛的应用。
在许多应用领域,绝对的序关系已经逐渐被等级制代替。在精细化的评分体制下,排名和数字刺激着人们敏感的神经。近些年,越来越多的机构逐渐改革评价体系,如英国在2011年实施食品卫生评级制[18],清华大学在2015年使用等级制取代百分制分数[19]。
诸多事实证明,评级制在一定程度上更适合作为评价的标准。本文也选用评级制对对象进行评价,即结合了三支决策的思想,将每个属性、每个对象都分成好(Good)、中(Medium)、差(Poor)三级评价,也称之为三支决策。
2 问题描述在本文研究的问题中,每个层级的对象用集合来描述。每个对象在某层评价完成后,会根据其层级关系映射到所属下一级的对象中。具体运算时,前一级的评价结果会成为下一级对象的输入属性。
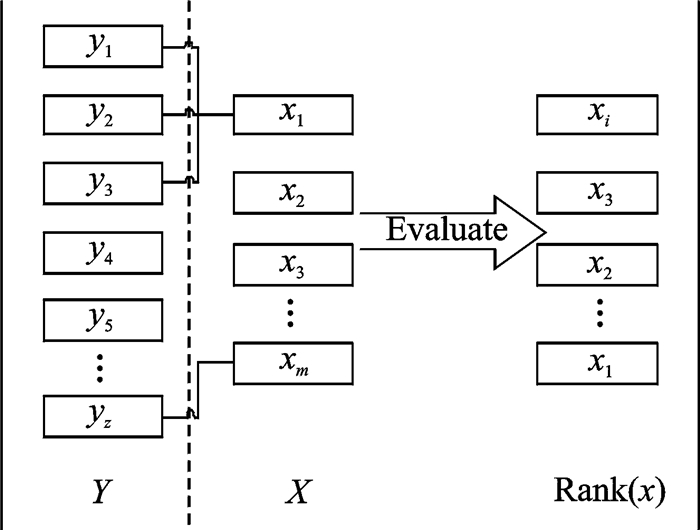
图 1给出了一个对象层级关系示例图。在Y这个层级,评价的对象有z个,并且每个对象都有一个好、中、差的评价结果。图 1中,Y级的对象y1, y2, y3属于X级的对象x1。这样,在X这个层级,对对象x进行评价时,Y层级的评价结果将被记录在X层级对象x的属性中,这类属性称为上层评价结果属性。也就是说,Rank(x)的值域是{好,中,差}。
|
图 1 对象层级关系实例 Fig. 1 Example of hierarchy relationships in objects |
Yoon和Hwang[2]认为对象的属性一般有3类:收益属性(Benefit attribute),这类属性值越大越好,如生产效率;消耗属性(Cost attribute),这类属性值越低越好,如亏损程度;不单调属性(Non monotonic attribute), 既有收益也有消耗,这类属性有一个最优值,属性值越靠近最优值越好。这种关于属性的分类方法被广泛应用在已有的研究工作中。
在本文提出的模型中,认为待评价的对象具有的属性可能有4类。除了上述3类,还有一类是融合了上层评价结果的“上层评价结果属性”。也就是说,评价对象集合中的每个对象都有一个来自上层评价的“上层评价结果属性”集合。这个“上层评价结果属性”集合包含3个属性,其值分别表示在这个评价对象集合中,其对应的上层对象属于好、中、差的三支评价结果的个数。例如,图 1中,如果y1, y2, y3分别被评价为“好”“好”“中”,则x1的“上层评价结果属性”集合对应的3个属性值就是2/|z|, 1/|z|, 0。
综上所述,本文研究的问题即为:针对可能具有如上所述4类评价属性的对象,寻找有效的对这些对象进行三支评价的方法。即:研究对象是一些待评价对象组成的集合X={x1, …, xm}。每个对象存在4类属性来描述,即属性集合A=A1∪A2∪A3∪A4={a1, …, an}。其中,A1表示“上层评价结果属性”集合,有|A1|=3且A1={a1, a2, a3},属性a1, a2, a3用于反映前一个层级在好、中、差三方面的评价结果值。A2,A3和A4分别表示收益属性、消耗属性和不单调属性。
3 三支决策评价模型本文提出的评价模型分为3个步骤:第1步选用AHP法计算属性权重;第2步预分类;第3步使用改进的TOPSIS三支评价方法对数据集进行评价,得到最终的三支分类结果。第1步的计算方法请参见文献[10],本节将详细介绍其他两个步骤。
3.1 预分类生活中当评价某个人时,往往都会先进行观察。仅仅凭借这次观察,对这个人所属的类别会有一个大概的判断;并且很多时候这种判断和最终的判断往往都相差不远。也就是说,如果将决策者与对象之间的第一次判断类似于“第一次见面”,那么这个“第一印象”在最终决策时也应该有一定的影响。因此,将这种思想借鉴到评价模型中,即首先对属性值、对象进行预分类。
预分类的过程包含两方面工作。首先,对每个属性值先进行预分类。给定评价属性的三支决策阈值α和β, 且α, β∈[0, 1]。则针对每个属性的三支决策规则为:距离最优值最近的α*100%个属性值为第1类(“好”);距离最优值最远的β*100%个属性值为第3类(“差”);其余为第2类(“中”)。接下来,针对每个对象,如果在其描述属性中某种类别出现次数最多,那就置其预分类类别为此类别。在这里,将属性值域离散到值域{1, 0.5, 0}。Rankpre(x)的值为{1, 0.5, 0}就分别对应于{好,中,差},这样赋值的意义在于与改进的TOPSIS三支评价方法融合时使最终计算结果的值域保持为[0, 1]。例如,如果对象x的属性中2出现的次数最多,那就初步认为x的类别是2,即Rankpre(x)=0.5。当出现类别个数一样多的时候,Rankpre(x)取值较低的一类,比如,当1和2同时最多的时候,有Rankpre(x)=0.5。
3.2 改进的TOPSIS三支评价方法在对对象预分类之后,接下来使用改进的TOPSIS三支评价方法进行评价。基本思想就是在已有的TOPSIS评价基础上通过加权的方式融合预分类的结果,结果以等级制给出, 具体步骤如下所述,其中步骤(1)—(4)来自文献[2],步骤(5)是本文新增加的步骤。
(1) 初始化评判矩阵R=(rij)m×n
矩阵R中rij表示第i个对象的第j个属性(评判指标)值,其中i∈[1, m],j∈[1, n], 则初始评判矩阵可以表示为
| $ \mathit{\boldsymbol{R}} = {\left( {{r_{ij}}} \right)_{m \times n}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1n}}}\\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2n}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{r_{m1}}}&{{r_{m2}}}& \cdots &{{r_{mn}}} \end{array}} \right] $ | (1) |
(2) 标准化(归一化)决策矩阵B=(bij)m×n
如前所述,属性类型不同,而且不同属性具有不同的量纲和量纲单位,不具备可比度,因此需要对属性进行归一化处理。相应的计算公式为
对于收益属性,有
| $ {b_{ij}} = \frac{{{r_{ij}} - \mathop {\min \left( {{r_{ij}}} \right)}\limits_j }}{{\mathop {\max \left( {{r_{ij}}} \right)}\limits_j - \mathop {\min \left( {{r_{ij}}} \right)}\limits_j }} $ | (2) |
对于消耗属性,有
| $ {b_{ij}} = \frac{{\mathop {\max \left( {{r_{ij}}} \right)}\limits_j - {r_{ij}}}}{{\mathop {\max \left( {{r_{ij}}} \right)}\limits_j - \mathop {\min \left( {{r_{ij}}} \right)}\limits_j }} $ | (3) |
对于不单调属性,有
| $ {b_{ij}} = {{\rm{e}}^{ - \frac{{{\theta ^2}}}{2}}},\theta = \frac{{\left( {{r_{ij}} - r_j^0} \right)}}{{{\sigma _j}}} $ | (4) |
式中:rj0为理想值(最有利),σj为每个属性与第j个属性值的标准差。
(3) 加权化标准矩阵P=(pij)m×n
令W[n]为根据AHP方法计算得到的属性权重矩阵。将矩阵B的列向量与W相乘,可得加权标准化决策矩阵P为
| $ \mathit{\boldsymbol{P}} = {\left( {{p_{ij}}} \right)_{m \times n}} = \left[ {\begin{array}{*{20}{c}} {{W_1}{b_{11}}}&{{W_2}{b_{12}}}& \cdots &{{W_n}{b_{1n}}}\\ {{W_1}{b_{21}}}&{{W_2}{b_{22}}}& \cdots &{{W_n}{b_{2n}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{W_1}{b_{m1}}}&{{W_2}{b_{m2}}}& \cdots &{{W_n}{b_{mn}}} \end{array}} \right] $ | (5) |
(4) 贴近度分析
| $ \left\{ \begin{array}{l} {P^ + } = \left\{ {\left( {\mathop {\max }\limits_n {p_{ij}}\left| {i \in {A_2} \cup {A_4}} \right.} \right),\left( {\mathop {\max }\limits_n {p_{ij}}\left| {i \in {A_3}} \right.} \right)} \right\}\\ {P^ - } = \left\{ {\left( {\mathop {\min }\limits_n {p_{ij}}\left| {i \in {A_2} \cup {A_4}} \right.} \right),\left( {\mathop {\max }\limits_n {p_{ij}}\left| {i \in {A_3}} \right.} \right)} \right\} \end{array} \right. $ | (6) |
式中P+与P-分别为正理想解和负理想解。
随后使用式(7)计算评判对象与正理想解和负理想解的距离。
| $ \left\{ \begin{array}{l} {D^ + }\left( {{x_i}} \right) = \sqrt {\sum\limits_{j = 1}^n {{{\left( {{p_{ij}} - p_j^ + } \right)}^2}} } \\ {D^ - }\left( {{x_i}} \right) = \sqrt {\sum\limits_{j = 1}^n {{{\left( {{p_{ij}} - p_j^ - } \right)}^2}} } \end{array} \right. $ | (7) |
式中:D+(xi),D-(xi)分别为待评判对象xi与正理想解和负理想解的距离;pj+和pj-分别为P+与P-相对应的元素。
最后,使用式(8)计算各个对象的贴近度
| $ \underline {{C^ + }} \left( {{x_i}} \right) = {D^ - }\left( {{x_i}} \right)/\left( {{D^ + }\left( {{x_i}} \right) + {D^ - }\left( {{x_i}} \right)} \right) $ | (8) |
显然,0≤
(5) 三支分类Rank
给定预分类结果权重ω1,贴近度计算值权重ω2。那么,评价结果计算公式为
| $ {\rm{Rank}}\left( {{x_i}} \right) = {\omega _1}{\rm{Ran}}{{\rm{k}}_{{\rm{pre}}}}\left( {{x_i}} \right) + {\omega _2}\underline {{C^ + }} \left( {{x_i}} \right) $ | (9) |
显然,0≤Rank(xi)≤1。
根据给定的三支评价阈值α和β,得到最终的评价分类结果。Rank(xi)值最高的α*100%个对象为第1类;Rank(xi)值最小的β*100%个对象为第3类;其余为第2类,分别置第1,2,3类对象Rank(xi)值为{1,2,3}。计算结果向上取整。
4 实例分析本节用一个实例来说明所提方法的评价过程。数据集来自文献[20],是一个关于人力资源选择问题。表 1描述了17个对象的客观属性,表 2给出了4位专家在2个客观属性上的评分值。在这个例子中的7个属性都为收益属性,分别为Language test (LT),Professional test (PT),Safety rule test (SRT),Professional skills (PS),Computer skills (CS),Panel interview (PI),1-on-1 interview (1-on-1)。
| 表 1 客观属性 Tab. 1 Objective attributes |
| 表 2 主观属性 Tab. 2 Subjective attributes |
为了反映本文所描述的对象具有层级关系,这里的每个对象都具有来自前一层级的评价值,即具有属性Good,Medium,Poor的值。
在得到数据集后,首先根据专家打分计算属性权重。为了方便与原文对比,由于原文未给出专家打分矩阵,在这里直接使用原文中专家给出的属性权重。由于本文所提出的方法新增加了A1类属性,也就是上层结果评价属性,因此从7个属性权重中抽取十分之一赋予这3个属性,形成新的属性权重集合如表 3所示。当然,如果在有原始打分信息的情况下,可以使用AHP方法来形成属性权重。
| 表 3 属性权重 Tab. 3 Weight on attributes |
在开始评价前,需要人为设置阈值以及式(9)的权值。决策者可以根据自己的需求选择每个类中对象的比例以及两次分类的权重。α和β代表值域为{好}和{差}的对象占总评价对象个数的比例。ω1和ω2代表预分类权重和改进的TOPSIS三支评价方法权重。
然后,对所有属性和对象进行预分类,本文设定α=0.2和β=0.8,分类结果如表 4所示, 其中,Rankpre表示预分类结果。
| 表 4 预分类 Tab. 4 Pre-classification |
最后,使用本文提出的改进的TOPSIS方法进行评价,通过式(1~9)的计算得到最终的排名。本文设定Rankpre权重ω1=0.2,
| 表 5 评价结果 Tab. 5 Evaluation results |
此外,表 5也对比了本文方法与文献[20]的评价结果。为了便于比较分析,将记录对象的有关值按文献[20]的评价结果值进行排序。从表 5可以看出,本文的评价结果与原文评价结果大致相同,但还是存在差别。在本文分的3个类中,第1类中有3个对象与原评价结果相同;第2类中有5个对象与原评价结果相同;第3类中有2个对象与原评价结果相同。原文中排名为4的对象在本文中属于第2类,也就是评价为{中},而原本排名为5的对象则属于第1类。这种现象有可能是因为他们继承了上层层级评价结果值的影响造成的。除此之外,第3类的对象也与原文的排名略有不同。同时可以发现,两个评价中评价不同的对象都处于每个类的边界。笔者认为,出现这种偏差的原因在于对原始数据进行了整合,使其满足本模型的需求,比如权重的整合以及上层评价结果的构造。实例分析说明,本文提出的基于TOPSIS的三支决策评价模型有效。
5 结束语本文针对评价对象之间具有层级关系的问题,提出了一种基于TOPSIS的三支决策评价模型。该模型与已有模型的主要不同点在于:对象具有层级关系,上层评价结果会影响下层(当前层)的评价;评价值不是给出严格的序关系,而是给出决策者关注的类别关系。但是,鉴于数据采集的原因,本文方法还未在真实数据上进行验证,只是给出了其在公开数据上的应用。而且因为数据集的特殊性,实例分析中只用到了两类属性,事实上本文方法针对4类属性都可以计算。接下来,该模型中的具体实现步骤还需要进一步完善,以适应真实的案例评价。
| [1] |
周海平, 黄凑英, 刘妮, 等. 基于评分预测的协同过滤推荐算法[J]. 数据采集与处理, 2016, 31(6): 1234-1241. Zhou Haiping, Huang Couying, Liu Ni, et al. Collaborative filtering recommendation algorithm based on rating prediction[J]. Journal of Data Acquisition and Processing, 2016, 31(6): 1234-1241. |
| [2] |
Hwang C L, Yoon K. Methods for multiple attribute decision making[M]. [S.l.]: Springer Berlin Heidelberg, 1981: 58-191.
|
| [3] |
Chen S J, Hwang C L. Fuzzy multiple attribute decision making methods[M]. [S.l.]: Springer Berlin Heidelberg, 1992: 289-486.
|
| [4] |
Boran F E, Genc S, Kurt M, et al. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method[J]. Expert Systems with Applications, 2009, 36(8): 11363-11368. DOI:10.1016/j.eswa.2009.03.039 |
| [5] |
Büyüközkan G, Çifçi G. A novel hybrid MCDM approach based on fuzzy DEMATEL, fuzzy ANP and fuzzy TOPSIS to evaluate green suppliers[J]. Expert Systems with Applications, 2012, 39(3): 3000-3011. DOI:10.1016/j.eswa.2011.08.162 |
| [6] |
Büyüközkan G, Güleryüz S. An application of intuitionistic fuzzy TOPSIS on mobile phone selection[C]//Fuzzy Systems (FUZZ-IEEE), 2015 IEEE International Conference on.[S.l.]: IEEE, 2015: 1-8.
|
| [7] |
Solanki R, Gulati G, Tiwari A, et al. A correlation based Intuitionistic fuzzy TOPSIS method on supplier selection problem[C]//Fuzzy Systems (FUZZ-IEEE), 2016 IEEE International Conference on.[S.l.]: IEEE, 2016: 2106-2112.
|
| [8] |
Madi E N, Garibaldi J M, Wagner C. An exploration of issues and limitations in current methods of TOPSIS and fuzzy TOPSIS[C]//Fuzzy Systems (FUZZ-IEEE), 2016 IEEE International Conference on.[S.l.]: IEEE, 2016: 2098-2105.
|
| [9] |
陆伟锋, 唐厚头. 关于多属性决策TOPSIS方法的一种综合改进[J]. 统计与决策, 2012(19): 38-40. |
| [10] |
Wind Y, Saaty T L. Marketing applications of the analytic hierarchy process[J]. Management Science, 1980, 26(7): 641-658. DOI:10.1287/mnsc.26.7.641 |
| [11] |
Al-Harbi K M A S. Application of the AHP in project management[J]. International Journal of Project Management, 2001, 19(1): 19-27. DOI:10.1016/S0263-7863(99)00038-1 |
| [12] |
Wang J W, Cheng C H, Huang K C. Fuzzy hierarchical TOPSIS for supplier selection[J]. Applied Soft Computing, 2009, 9(1): 377-386. DOI:10.1016/j.asoc.2008.04.014 |
| [13] |
Liang D, Liu D, Kobina A. Three-way group decisions with decision-theoretic rough sets[J]. Information Sciences, 2016, 345: 46-64. DOI:10.1016/j.ins.2016.01.065 |
| [14] |
Zhou B, Yao Y, Luo J. Cost-sensitive three-way email spam filtering[J]. Journal of Intelligent Information Systems, 2014, 42(1): 19-45. DOI:10.1007/s10844-013-0254-7 |
| [15] |
Yao J T, Azam N. Web-based medical decision support systems for three-way medical decision making with game-theoretic rough sets[J]. IEEE Transactions on Fuzzy Systems, 2015, 23(1): 3-15. DOI:10.1109/TFUZZ.2014.2360548 |
| [16] |
杨霁琳, 张贤勇, 唐孝. 基于三支决策的模糊信息系统OWA算子参数选择[J]. 数据采集与处理, 2016, 31(6): 1156-1163. Yang Jilin, Zhang Xianyong, Tang Xiao. Three-way decisions based parameter selection of OWA operators in fuzzy information system[J]. Journal of Data Acquisition and Processing, 2016, 31(6): 1156-1163. |
| [17] |
于洪, 王国胤, 李天瑞, 等. 三支决策:复杂问题求解方法与实践[M]. 北京: 科学出版社, 2015.
|
| [18] |
杨艳.英国实施食品卫生评级制[N].中国食品安全报, 2011-06-25 B04.
|
| [19] |
Tsinghua.edu.cn.清华缘何告别百分制?[EB/OL]. [2016-12-24]. http://news.tsinghua.edu.cn/publish/thunews/9669/2015/20150525175754264220001/20150525175754264220001_.html.
|
| [20] |
Shih H S, Shyur H J, Lee E S. An extension of TOPSIS for group decision making[J]. Mathematical and Computer Modelling, 2007, 45(7): 801-813. |
 2018, Vol. 33
2018, Vol. 33

