引言

多项式相位信号在雷达、声呐、地震波和无线通信等领域都有广泛的应用^[1-8]。作为一种多项式相位信号，线性调频信号(Linear FM signal, LFM)也出现在这些科学和工程领域。对于固定的接收机，LFM信号可用来估计移动目标的运动轨迹；另外，在一定条件下，它也提供了一种成功的数字调制方法。由于它的广泛应用，很多研究者都比较关注于它的检测与参数估计，也提出了很多理论与方法^[9-12], 这些方法中有些研究者提出了用稀疏分解来实现对LFM信号的参数估计，比如文献[6]使用Gabor原子实现对LFM信号的参数估计，其运算量大，在确定了最匹配的原子后，需采用Hough变换对处于直线分布的原子进行参数提取，这种变换也进一步加大了运算量。另外采用Gabor原子来实现LFM信号的稀疏分解，从结果来看，它的稀疏度并不高，并不利于对LFM信号的参数估计。文献[11, 12]采用了与LFM信号结构相同的Chirplet原子来实现对LFM信号的稀疏分解，然而它的运算量依然很大，其复杂度为O(N²)。

贪婪方法和凸松弛方法是信号稀疏分解的两类主要分解方法，前者的主要代表是匹配追踪(Matching pursuit, MP)^[13]，后者为基追踪(Basis pursuit, BP)^[14]。不论是贪婪方法或者凸松弛方法，过完备字典中原子都存在数量巨大的问题，从而出现较高的计算复杂度。许多研究者为了提高稀疏分解速度，提出了相应的智能算法，比如遗传算法和粒子群算法^[15-18]，然而由于这些智能算法中存在一定的随机性，因此它们在某些应用场合可能并不适用，并且即使采用了这些智能算法，其分解速度也有待进一步的提高。另外，基于原子集合划分的快速算法也被一些研究者提出^[19]，虽然，随机性问题在这类快速算法中不存在，但这类快速算法主要以Gabor原子为研究对象，以减少原子库中原子数量为目的，收敛速度和稀疏分解速度仍然需要进一步的提高。还有一些研究者利用分数阶傅里叶变换对多项式相位信号进行稀疏分解^{[20, 21]}, 虽然分数阶傅里叶变换对多项式相位信号具有能量聚集特性，能反映出信号在时域和频域的信息，但它在稀疏分解中仍然面临过完备字典中原子数量庞大的问题。

为了减少冗余字典中的原子数量，加快LFM信号稀疏分解速度，同时提高稀疏分解的收敛速度，本文提出了一种LFM信号快速稀疏分解算法。这种算法采用级联字典的方式，在每个字典中，其原子结构更接近于LFM信号，并利用快速的傅里叶变换，极大加快了LFM信号的稀疏分解和它的收敛速度。这种方法通过实验结果证实，不仅稀疏分解速度快、稀疏度高，而且有利于LFM信号的参数估计。

1 信号的稀疏分解

稀疏分解就是信号用较少的原子通过线性组合来表示^{[13, 22]}，它的模型表达为

$ y = \mathit{\Phi }\alpha \;满足\left\| \alpha \right\| $

(1)

式中：信号y∈R^N×1，α∈R^M×1；||α||₀为稀疏度，||α||₀=M, 字典Φ∈R^N×M。对于式(1)的求解，只能用组合方法，需要系统地检验所有项的潜在组合，这是非确定性问题(Non-deterministic polynomial, NP)难的组合优化问题。为了解决该问题，Mallat和Zhang提出了利用贪婪技术的匹配追踪算法^[9]。匹配追踪的具体做法为：设定初始残余信号R⁰y等于y，接着计算R⁰y与冗余字典Φ中所有原子的内积，并在这些内积中寻找最大内积的原子，通过该原子得到分解系数α₀，然后计算下一步残余信号R¹y和逼近。在第k步，求解α_k=[R^ky, g_k]=max|[R^ky, g_m]|，同时计算新的残余信号R^k+1y和新的逼近，即R^k+1y=R^ky－α_kg_k和$y = \sum\limits_{i = 1}^k {{\alpha _i}{g_i}} + {R^{k + 1}}y$。

由于Gabor原子频率不随时间变化，对于LFM信号的稀疏分解，采用时频域内聚集性好的Chirplet原子通过稀疏分解更有利于LFM信号的参数估计，并且更稀疏。Chirplet原子可表示为

$ {g_r}\left( {s,u,\xi ,c} \right) = \frac{1}{{\sqrt s }}g\left( {\frac{{t - u}}{s}} \right)\exp \left[ {{\rm{j}}\left( {\xi \left( {t - u} \right) + \frac{c}{2}{{\left( {t - u} \right)}^2}} \right)} \right] $

(2)

式中：s和u分别为尺度因子和信号的时间中心; ξ和c分别为频率中心和信号调频斜率。

2 LFM信号的快速稀疏分解算法

设LFM信号模型为^[23]

$ y\left( t \right) = A\exp \left\{ {{\rm{j}}2{\rm{ \mathsf{ π} }}\left( {{f_0}t + \frac{{K{t^2}}}{2}} \right)} \right\} $

(3)

式中：f₀为初始频率，K为调频斜率，A为信号幅度。当A=1时，离散LFM信号模型表示为

$ y\left( n \right) = \exp \left\{ {{\rm{j}}2{\rm{ \mathsf{ π} }}\left[ {{f_0}n + \frac{{K{n^2}}}{2}} \right]} \right\} $

(4)

对LFM信号，采用Chirplet原子进行稀疏分解时，由于采用匹配追踪算法时需要对原子进行归一化处理，即

$ \begin{array}{*{20}{c}} {{{g'}_r}\left( t \right) = \frac{{{g_r}\left( t \right)}}{{\sqrt {{g_r}\left( t \right)_2^2} }} = }\\ {\frac{{g\left( {\frac{{t - u}}{s}} \right)\exp \left[ {{\rm{j}}\left( {\xi \left( {t - u} \right) + \frac{c}{2}{{\left( {t - u} \right)}^2}} \right)} \right]}}{{{{\left[ {{{\left\{ {g\left( {\frac{{t - u}}{s}} \right)\exp \left[ {{\rm{j}}\left( {\xi \left( {t - u} \right) + \frac{c}{2}{{\left( {t - u} \right)}^2}} \right)} \right]} \right\}}^{ - {\rm{T}}}} \times \left\{ {g\left( {\frac{{t - u}}{s}} \right)\exp \left[ {{\rm{j}}\left( {\xi \left( {t - u} \right) + \frac{c}{2}{{\left( {t - u} \right)}^2}} \right)} \right]} \right\}} \right]}^{\frac{1}{2}}}}}} \end{array} $

(5)

从式(5)可以看出，原子的归一化处理使得尺度因子失去了作用，另外，为了使构建的原子更接近LFM信号的特点，可进一步去掉高斯窗函数$g\left( {\frac{{t - u}}{s}} \right)$和位移因子u，根据LFM信号模型，过完备字典的原子可表示为

$ {g_\gamma } = \left( {\frac{1}{N}} \right)\exp \left[ {{\rm{j}}2{\rm{ \mathsf{ π} }}\left( {{f_u}n + \frac{{{K_v}{n^2}}}{2}} \right)} \right] $

(6)

式中：f_u为LFM信号的起始频率，K_v为LFM信号的调频斜率。根据搜索精度和范围，以均匀取值的方式，设定f_u的搜索个数为U，K_v搜索个数为V，可构造为

$ {G_f}{\left\{ {{g_\gamma }} \right\}_{\gamma \in \mathit{\Gamma }}} = \left[ {\begin{array}{*{20}{c}} {{g_{\gamma = \left( {{f_1},{K_1}} \right)}}}&{{g_{\gamma = \left( {{f_1},{K_2}} \right)}}}& \cdots &{{g_{\gamma = \left( {{f_1},{K_V}} \right)}}}\\ {{g_{\gamma = \left( {{f_2},{K_1}} \right)}}}&{{g_{\gamma = \left( {{f_2},{K_2}} \right)}}}& \cdots &{{g_{\gamma = \left( {{f_2},{K_V}} \right)}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{g_{\gamma = \left( {{f_U},{K_1}} \right)}}}&{{g_{\gamma = \left( {{f_U},{K_2}} \right)}}}& \cdots &{{g_{\gamma = \left( {{f_U},{K_V}} \right)}}} \end{array}} \right] $

(7)

式中：γ=(f_u, K_v)为原子时频参数组，Γ为γ的集合，冗余字典的原子个数为U×V，假设信号长度N=256，U=V=500，则有U×V=250 000，很明显原子个数比信号长度N大得多。如果字典中采用Gabor原子，则原子数量为L_D=52(Nlog₂N+N－1)=119 756。可以看出，这种原子数量远远超过采用Gabor原子得到的原子数量，因此，为了加快稀疏分解速度，需要利用相应的算法来减少计算量，从而实现快速稀疏分解的目的。

根据匹配追踪算法，展开系数α₀的选取采用求解R⁰y与原子集合{g_m}的最大内积来获得，根据式(6)的原子，有

$ \begin{array}{*{20}{c}} {{\alpha _0} = \left[ {{R^0}y,{\psi _0}} \right] = \max \left| {\left[ {{R^0}y,{\psi _m}} \right]} \right| = }\\ {\max \left| {\sum\limits_{n = 1}^N {\frac{1}{N}\exp \left\{ {{\rm{j2 \mathsf{ π} }}\left[ {{f_0}n + \frac{{K{n^2}}}{2}} \right]} \right\}\exp \left[ { - {\rm{j2 \mathsf{ π} }}\left( {{f_u}n + \frac{{{K_v}{n^2}}}{2}} \right)} \right]} } \right| = }\\ {\max \left| {\sum\limits_{n = 1}^N {\frac{1}{N}\exp \left\{ {{\rm{j2 \mathsf{ π} }}\left[ {\left( {{f_0} - {f_u}} \right)n + \frac{{\left( {K - {K_v}} \right){n^2}}}{2}} \right]} \right\}} } \right|} \end{array} $

(8)

从式(8)可以看出，当f₀－f_u=0和K－K_v=0时，α₀必将取得最大值；当K－K_v=0且f₀－f≠0，$\exp \left\{ {{\rm{j}}2{\rm{ \mathsf{ π} }}\left[ {\left( {{f_0} - {f_n}} \right)n + \frac{{\left( {K - {K_v}} \right){n^2}}}{2}} \right]} \right\}$是一个正弦波信号，通过傅里叶变换，它必将在f=f₀－f_u取得最大值。

通过以上分析可知，当LFM信号的二次相位系数与调频斜率参量K_v匹配时，就有一个正弦波信号出现，这样就可以用快速傅里叶变换的方法来实现快速的稀疏分解。

由于采用式(6)的原子来构建过完备字典时原子数量庞大，下面将采用两个字典联合的方式对LFM信号进行稀疏分解。

根据式(6)，可得

$ {g_\gamma } = \left( {\frac{1}{N}} \right)\exp \left[ {{\rm{j2 \mathsf{ π} }}\left( {{f_u}n + \frac{{{K_v}{n^2}}}{2}} \right)} \right] = \left( {\frac{1}{N}} \right)\exp \left[ {{\rm{j2 \mathsf{ π} }}\frac{{{K_v}{n^2}}}{2}} \right]\exp \left[ {{\rm{j2 \mathsf{ π} }}{f_u}n} \right] $

(9)

根据式(7)，在构造第一个字典Φ₁中，可设定基于调频斜率参量K_v的原子，为

$ \left\{ \begin{array}{l} {g_{{\gamma _1}}} = \exp \left[ {{\rm{j2 \mathsf{ π} }}\frac{{{K_v}{n^2}}}{2}} \right]\\ {G_f}{\left\{ {{g_{{\gamma _1}}}} \right\}_{\gamma \in {\mathit{\Gamma }_1}}} = \left[ {\begin{array}{*{20}{c}} {{g_{{\gamma _1} = \left( {{K_1}} \right)}}}&{{g_{{\gamma _1} = \left( {{K_2}} \right)}}}& \cdots &{{g_{{\gamma _1} = \left( {{K_V}} \right)}}} \end{array}} \right] \end{array} \right. $

(10)

可以看出，字典Φ₁中原子的数量为U，因此有

$ \begin{array}{*{20}{c}} {{\alpha _0} = \left[ {{R^0}y,{\psi _0}} \right] = \max \left| {\left[ {{R^0}y,{\psi _m}} \right]} \right| = \\ \max \left| {\sum\limits_{n = 1}^N {\exp \left\{ {{\rm{j2 \mathsf{ π} }}\left[ {{f_0}n + \frac{{K{n^2}}}{2}} \right]} \right\}\exp \left[ { - {\rm{j2 \mathsf{ π} }}\frac{{{K_v}{n^2}}}{2}} \right]} } \right| = }\\ {\max \left| {\sum\limits_{n = 1}^N {\exp \left\{ {{\rm{j2 \mathsf{ π} }}\left[ {{f_0}n + \frac{{\left( {K - {K_v}} \right){n^2}}}{2}} \right]} \right\}} } \right|} \end{array} $

(11)

在式(11)中，当K－K_v越接近0，很明显，$\exp \left\{ {{\rm{j}}2{\rm{ \mathsf{ π} }}\left[ {{f_0}n + \frac{{\left( {K - {K_v}} \right){n^2}}}{2}} \right]} \right\}$越接近正弦信号，通过傅里叶变换其绝对值越大。从图 1可看出，当K－K_v=1.25×10^－10时，信号傅里叶变换的绝对值存在一个明显的尖峰，而K－K_v=1.25×10^－3和K－K_v=2.25×10^－3则没有出现这样的尖峰。很明显，当K－K_v越小，在信号傅里叶变换后的绝对值中存在的最大值也越大。

基于起始频率f_u来构建第2个字典Φ₂，为

$ \left\{ \begin{array}{l} {g_{{\gamma _2}}} = \exp \left[ {{\rm{j2 \mathsf{ π} }}{f_u}n} \right]\\ {G_f}{\left\{ {{g_{{\gamma _2}}}} \right\}_{\gamma \in {\mathit{\Gamma }_2}}} = \left[ {\begin{array}{*{20}{c}} {{g_{{\gamma _2} = \left( {{f_1}} \right)}}}&{{g_{{\gamma _2} = \left( {{f_2}} \right)}}}& \cdots &{{g_{{\gamma _1} = \left( {{f_U}} \right)}}} \end{array}} \right] \end{array} \right. $

(12)

对于式(12)中f_u参数的设定，根据傅里叶变换表达为

$ \left\{ \begin{array}{l} Y\left( k \right) = \sum\limits_{j = 1}^N {y\left( j \right)\omega _N^{\left( {j - 1} \right)\left( {k - 1} \right)}} \\ \;\;\;{\omega _N} = {{\rm{e}}^{\left( { - 2{\rm{ \mathsf{ π} i}}} \right)/N}} \end{array} \right. $

(13)

可以看出，f_u的设定对应于傅里叶变换中的ω_N，这就意味着可通过快速傅里叶变换来寻找字典Φ₂中最匹配的原子。

根据上面分析，得出LFM信号的快速稀疏分解算法为：

(1) 构造基于调频斜率参量K_v的字典Φ₁，其原子设为${g_{{\gamma _1}}} = \exp \left[ {{\rm{j}}2{\rm{ \mathsf{ π} }}\frac{{{K_v}{n^2}}}{2}} \right]$，根据搜索精度可设定原子的个数为V。

(2) LFM信号与每一个原子共轭相乘，并对乘积后的信号进行快速傅里叶变换。

(3) 求取所有傅里叶变换的最大值，其对应的原子即为最匹配的原子，并且最大值所对应的频率就是构建的基于起始频率f_u的第2个字典Φ₂中最匹配的原子频率。

(4) 根据Φ₁和Φ₂中最匹配的原子参数，得到LFM信号最匹配的原子。

3 算法复杂度分析

采用Gabor原子的冗余字典，其原子数量为${L_D} = \sum\limits_{j = 1}^{{{\log }_2}N} {\sum\limits_{p = 1}^{N \times {2^{ - j + 1}}} {\sum\limits_{k = 0}^{{2^{j + 1}}} {\sum\limits_{i = 0}^{12} 1 } } } $，简化为L_D=52(Nlog₂N+N－1)^[24]，可以看出，原子数量L_D是一个非常大的数，例如当信号长度N=1 024，则原子数量L_D=585 676，这使得稀疏分解的计算量很大。而在本文提出的算法里，由于采用了级联字典，对比于采用一个字典，整个原子的数量极大减少了。其级联字典中原子的数量由参数范围和设定的精度决定，与信号的长度无关，比如K_v的搜索范围设定为1×10^－3, 5×10^－3，精度设为1×10^－6，则冗余字典Φ₁中原子数量为4 001个，而字典Φ₂中原子的数量由快速傅里叶变换的点数决定，其原子数量也是一个比较小的数，比如信号长度为712，为了提高快速傅里叶变换的精度，设定其点数为1 024，则Φ₂中原子个数为1 024。这样总的原子数为5 025个，这个数与采用Gabor原子相比，其计算复杂度必然大大减少。

从算法的复杂度看，采用Gabor原子的计算复杂度为O(N⁴)，而本文提出的算法，对于第1个字典，它的稀疏分解复杂度为O(N)。对于第2个字典，由于每个原子的处理都要用到FFT，而FFT的计算复杂度为O(NlogN)，因此它的稀疏分解复杂度为O(N²logN)。

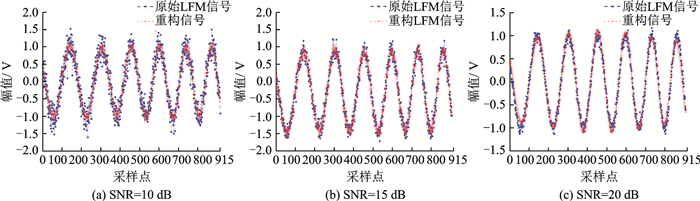
4 实验及结果分析

为了验证算法的快速性，实验中采用主频为3.40 GHz的双核Intel(R) Core(TM) i7-6700 CPU计算机，软件环境为Matlab 7.0。实验设定LFM信号为y=exp(j(a₂t²+a₁t))+u(t)，其中u(t)表示加性高斯白噪声。信号的信噪比分别设为SNR=10, 15和20 dB，参数a₂, a₁设为(a₂, a₁)=(1.25×10^－3, 4.487 4)，采样时间间隔t_s=1 s，信号长度设为N=915，根据本文提出的快速稀疏分解算法，首先构造字典Φ₁，其原子设为${g_{{\gamma _1}}} = \exp \left[ {{\rm{j}}2{\rm{ \mathsf{ π} }}\frac{{{K_v}{n^2}}}{2}} \right]$，其中K_v的搜索范围设为$\frac{{\left[ {1 \times {{10}^{ - 3}},\;2 \times {{10}^{ - 3}}} \right]}}{{\rm{ \mathsf{ π} }}}$, 搜索精度设为$\frac{{\left( {1 \times {{10}^{ - 6}}} \right)}}{{\rm{ \mathsf{ π} }}}$，则原子个数为1 000。然后，进行算法的其余3步，找到最匹配的原子。在第3步设定字典Φ₂中原子个数时，设定原子个数为1 024个。在稀疏分解中，设定迭代次数为20次。重构信号如图 2所示，从图 2可以看出，采用本文提出基于级联字典的快速稀疏分解算法，重构信号能较好地逼近初始信号。

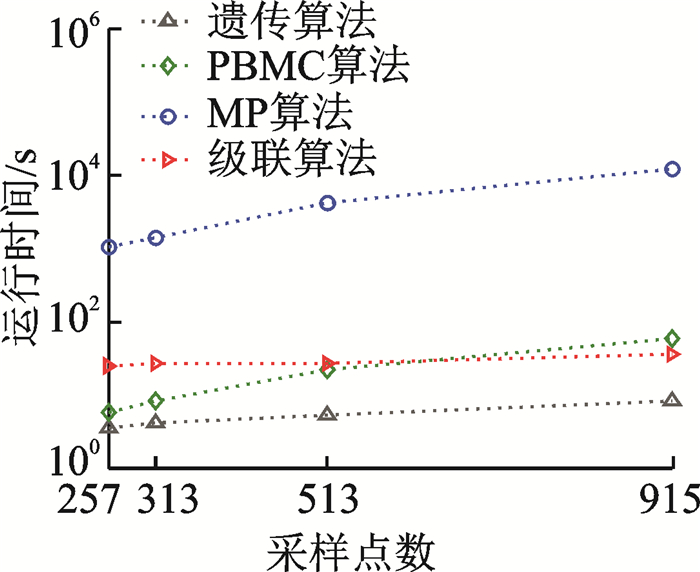
对于本文提出的算法，为了更好地体现它的快速性和收敛速度，以基于Gabor原子的匹配追踪算法，基于遗传算法的快速稀疏分解以及最近提出的基于调制相关划分(Partition the over-complete dictionary based on modulation correlation，PBMC)^[19]的快速稀疏分解进行对比。首先考虑的是在相同迭代次数条件下不同信号长度的运算时间，设定稀疏分解的迭代次数为100次，信号长度分别定义为257，313，513和915，这4种算法的计算时间如图 3所示，从图 3可知，对于相同的迭代次数，基于遗传算法的信号稀疏分解速度很明显最快，最慢的是采用MP算法进行的信号稀疏分解，其计算复杂度必然是最高的。而随着信号长度的增加，从图 3中的两条相交曲线可以看出，在信号长度为513时，PBMC算法的稀疏分解时间与本文所提出的基于级联字典的快速稀疏分解算法所用时间比较接近，之后逐渐超过，在信号长度为915时，计算时间超过比较明显。

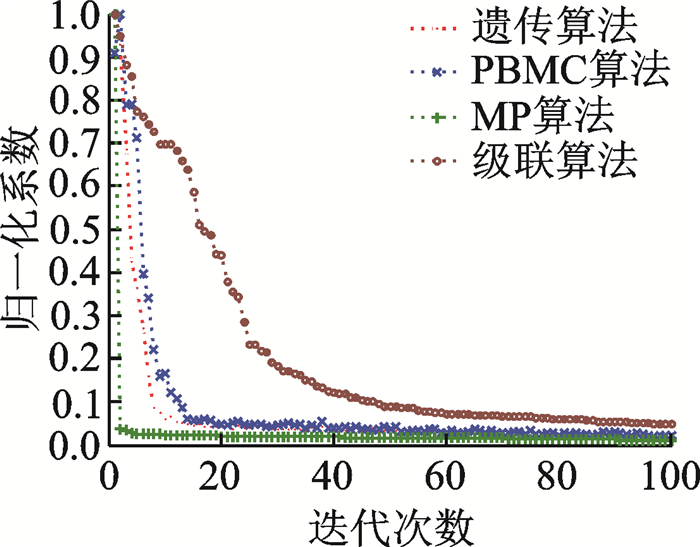
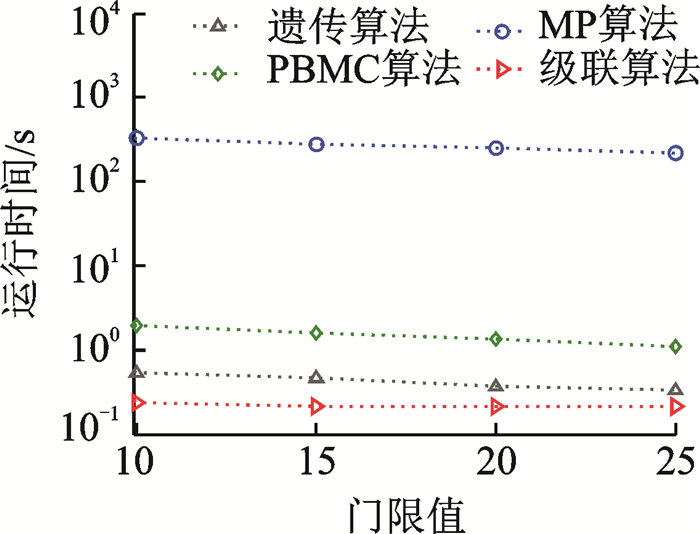
对于相同的迭代次数，本文提出的快速算法，虽然它的稀疏分解速度不是最快的，然而这种算法的收敛速度非常快，如图 4所示。从图 4可以看出，通过4种算法得到的归一化分解系数比较，可以看出本文提出的快速算法进行稀疏分解时，其分解系数的绝对值比其他算法向零衰减的速度要快得多，这意味着根据相同的稀疏分解门限，采用该算法进行稀疏分解，所需的迭代次数最少。对此，设定稀疏分解门限为10，15，20和35，则4种算法在信号长度为257时所用的时间如图 5所示。可以看出，在相同的信号长度下，对于相同的稀疏分解门限，本文所提出的算法比其他3种算法都有较快的稀疏分解速度，其中比PBMC算法快1个数量级，比MP算法快4个数量级，而且随着信号长度的增加，表现更加突出。从实验结果来看，本文提出的快速算法不仅具有快速的稀疏分解特性，而且有很好的收敛性。

5 结束语

本文提出的快速稀疏分解算法主要根据LFM信号的特点，采用级联字典的方式，对比采用一个冗余字典，极大地减少了原子数量，同时利用快速傅里叶变换，大大加快了稀疏分解的速度，同时也具有较好的收敛速度。在分解速度和收敛速度上，本文提出的快速稀疏分解算法在实验中通过对比显示了它具有较好的性能。另外，本文提出的针对LFM信号的快速稀疏分解算法，不仅对LFM信号的稀疏分解有重要意义，而且对于LFM信号的检测和参数估计，同样具有重要的意义。