引言

多输入多输出(Multiple-input multiple-output，MIMO)雷达的相关研究已成为学术界关注的重点。该种体制的雷达在发射和接收两端均配备多根天线用于发射和接收信号，相比于传统体制雷达，其自由度大幅提高，在抗干扰性能、参数估计准确度、空间分辨率等方面有显著提升^[1-4]。

波达角(Direction of arrival, DOA)估计是MIMO雷达的一项基本任务，以此为基础，MIMO雷达中的多参数估计研究，如波达角和多普勒频率联合估计，也日益受到学术界重视。已有的工作多以经典的子空间算法为基础扩展而来，如多重信号分类算法(Multiple signal classification，MUSIC)^[5-8]、基于旋转不变技术的估计算法(Estimation method of signal parameters via rotational invariance techniques，ESPRIT)^[9-11]、传播算子算法(Propagator method, PM)^[12-13]等。MUSIC算法^[5]是一种经典的超分辨算法，其利用噪声子空间和方向矢量之间的正交性，通过谱峰搜索得到参数估计。文献[6]将经典MUSIC算法推广到MIMO雷达领域。虽然MUSIC算法具有估计精度高、可适用于任意构型的阵列的优点，但其谱峰搜索运算带来了巨大复杂度、且要求阵列各阵元位置完全已知，这些缺点使得MUSIC算法难以应用到实际中。目前基于MUSIC算法的研究以降低复杂度为主要研究目标^[7-8]。不同于MUSIC，ESPRIT算法^[9-11]利用了阵列流型的旋转不变特性和信号子空间，实现了对DOA的闭式解估计。与MUSIC相比，ESPRIT的计算复杂度大大降低。文献[14]针对二维DOA和频率联合估计，提出了一种扩展的ESPRIT算法，但其需要额外配对。文献[15]研究了双基地MIMO下的DOA和频率估计问题，其利用时延采样之间的旋转不限性实现了参数的闭式解估计，且可自动配对。MUSIC算法和ESPRIT算法通常均通过对接收信号的奇异值分解(Singular value decomposition, SVD)或对接收信号协方差矩阵的特征值分解(Eigen value decomposition, EVD)得到对特征子空间的估计。PM算法通过对接收信号矩阵(或接收信号的协方差矩阵)的简单运算得到传播算子，并由传播算子估计特征子空间，因而其无需SVD或EVD，节省了计算复杂度。低复杂度的优点使得PM算法在雷达、通信等对数据处理实时性要求较高的领域具有广泛应用前景。

在实际的电磁环境中，多径传播现象导致信号常呈现相干特性，这使得协方差矩阵存在秩亏欠，经典的子空间算法因此将不能有效估计相干信源的DOA。学术界对于相干信号的参数估计已开展了大量的研究工作。文献[16, 17]提出了一种有效的空间平滑技术(Spatial smoothing, SS)，其将均匀分布的阵列分成一系列相同而又重合的子阵列，通过计算各子阵列平均协方差的方式保证了协方差矩阵的非奇异特性。文献[18-21]研究了改进的空间平滑技术，降低了阵列孔径损失。文献[22]将ESPRIT算法和前向空间平滑(Forward spatial smoothing, FSS)技术结合，解决了单基地MIMO雷达中的DOA和多普勒频率联合估计问题。除了空间平滑技术之外，文献[23]通过构造特殊的Toeplitz矩阵实现了信号的解相干，为MIMO雷达下相干信号参数估计提供了另一种思路。

PM方法复杂度相比MUSIC，ESPRIT有优势。基于PM方法，本文提出了一种降维的前向平滑-传播算子(RD-FSS-PM)算法。所提算法首先对接收信号进行降维变换，剔除了冗余数据；随后，利用前向空间平滑技术和PM算法实现了信号的解相干，以及波达角和多普勒频率的联合估计，且无需额外配对。所提算法对DOA和多普勒估计均可通过闭式解求解，无需谱峰搜索，也无需SVD或者EVD分解运算，复杂度较低。与传统的FSS-PM法相比，所提算法降低计算复杂度的同时，波达角估计精度改善而多普勒估计频率接近。此外，本文进行了误差分析，给出了详尽的仿真实验以验证算法的估计性能。

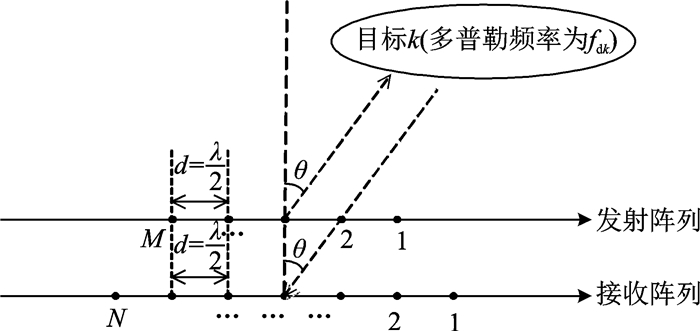
1 单基地MIMO雷达数据模型

如图 1所示，假设一单基地MIMO雷达系统在收发两端采用均匀线阵，其天线数分别为M和N，相邻天线之间的距离为d，且d≤λ/2，λ为发射波形波长。在发射端，M根天线同时发射具有相同带宽和载频的正交波形信号。假设空间中存在K个远场目标(信源数K已知，若未知，其估计方法参考文献[17-20])，其中相干目标和非相干目标同时存在，K个目标的波达角分别为θ =[θ₁, …, θ_K]^T。此时，接收端信号输出经匹配滤波器滤波之后可表示为如下矩阵形式

$ \mathit{\boldsymbol{x}}\left( t \right) = \mathit{\boldsymbol{A}}\left( \theta \right)\mathit{\boldsymbol{S}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right) $

(1)

式中：A=[a_r(θ₁)⊗a_t(θ₁), …, a_r(θ_K)⊗a_t(θ_K)]为MN×K的阵列流型矩阵，a_t(θ_k)=[1, e^{-j2πdsinθ_k/λ}, …, e^{-j(M-1)2πdsinθ_k/λ}]^T和a_r(θ_k)=[1, e^{-j2πdsinθ_k/λ}, …, e^{-j(N-1)2πdsinθ_k/λ}]^T为对应于第k个目标的发射和接收方向矢量，⊗表示克罗内克积(Kronecker produce); S(t)=[s₁(t), s₂(t), …, s_K(t)]^T∈C^K×1为回波信号矢量, 其第k个元素s_k(t)=β_ke^{j2πf_dkt/f_s}，β_k为第k个点目标的雷达截面系数(Radar cross section，RCS)，f_dk为第k个点目标的多普勒频率，f_s为发射波形的脉冲重复频率; n(t)∈C^MN×1表示加性高斯白噪声。

阵列流型矩阵A可以表示成

$ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{A}}_{\rm{R}}} \circ {\mathit{\boldsymbol{A}}_{\rm{T}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{\rm{T}}}{D_1}\left( {{\mathit{\boldsymbol{A}}_{\rm{R}}}} \right)}\\ {{\mathit{\boldsymbol{A}}_{\rm{T}}}{D_2}\left( {{\mathit{\boldsymbol{A}}_{\rm{R}}}} \right)}\\ \vdots \\ {{\mathit{\boldsymbol{A}}_{\rm{T}}}{D_N}\left( {{\mathit{\boldsymbol{A}}_{\rm{R}}}} \right)} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{\rm{T}}}}\\ {{\mathit{\boldsymbol{A}}_{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}\\ \vdots \\ {{\mathit{\boldsymbol{A}}_{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{N - 1}}} \end{array}} \right] $

(2)

式中：A_T=[a_t(θ₁), a_t(θ₂), …, a_t(θ_K)]∈C^M×K和A_R=[a_r(θ₁), a_r(θ₂), …, a_r(θ_K)]∈C^N×K分别为包含了K个发射和接收阵列流型矢量的范德蒙(Vandermode)矩阵; $ \circ $表示Khatri-Rao积; D_i(A_R)取A_R的第i行并将其对角化; Φ=D₂(A_R)=diag(e^{-j2πdsinθ₁/λ}, …, e^{-j2πdsinθ_K/λ})∈C^K×K。

2 算法推导 2.1 降维变换

定义一个MN×(M+N-1)的变换矩阵G^[24]为

$ \mathit{\boldsymbol{G}} = \left[ {\left. {\begin{array}{*{20}{c}} {\left. {\begin{array}{*{20}{c}} 1&0& \cdots &0&0&0& \cdots &0\\ 0&1& \cdots &0&0&0& \cdots &0\\ \vdots&\vdots&\ddots&\vdots&\vdots&\ddots&\vdots &{}\\ 0&0& \cdots &1&0&0& \cdots &0 \end{array}} \right\}M}\\ {\left. {\begin{array}{*{20}{c}} 0&1&0& \cdots &0&0& \cdots &0\\ 0&0&1& \cdots &0&0& \cdots &0\\ \vdots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots &{}\\ 0&0&0& \cdots &0&1& \cdots &0 \end{array}} \right\}M}\\ \vdots \\ {\left. {\begin{array}{*{20}{c}} 0& \cdots &0&1&0&0& \cdots &0\\ 0& \cdots &0&0&1&0& \cdots &0\\ \vdots&\ddots&\vdots&\vdots&\vdots&\vdots&\ddots&\vdots \\ 0& \cdots &0&0&0&0& \cdots &1 \end{array}} \right\}M} \end{array}} \right\}M \times N} \right] $

(3)

对应于第k个目标的阵列流型矢量a_r(θ_k)⊗a_t(θ_k)可以表示为

$ {\mathit{\boldsymbol{a}}_{\rm{r}}}\left( {{\theta _k}} \right) \otimes {\mathit{\boldsymbol{a}}_{\rm{t}}}\left( {{\theta _k}} \right) = \mathit{\boldsymbol{Gb}}\left( {{\theta _k}} \right) $

(4)

式中b(θ_k)=[1, e^{-j2πdsinθ_k/λ}, …, e^{-j2π(M+N-2)dsinθ_k/λ}]^T。定义W=G^HG，其详细表达式为

$ \mathit{\boldsymbol{W}} = {\rm{diag}}\left( {1,2, \cdots ,\underbrace {\min \left( {M,N} \right), \cdots ,\min \left( {M,N} \right)}_{\left| {M - N} \right| + 1}, \cdots ,2,1} \right) $

(5)

对接收信号x(t)右乘W^-1G^H矩阵可将x(t)虚拟成一个由(M+N-1)个阵元构成的均匀线阵(Uniform linear array, ULA)的接收信号，即

$ \mathit{\boldsymbol{y}}\left( t \right) = {\mathit{\boldsymbol{W}}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{H}}}\mathit{\boldsymbol{x}}\left( t \right) = {\mathit{\boldsymbol{W}}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{H}}}\left( {\mathit{\boldsymbol{G}}\left[ {\mathit{\boldsymbol{b}}\left( {{\theta _1}} \right), \cdots ,\mathit{\boldsymbol{b}}\left( {{\theta _K}} \right)} \right]\mathit{\boldsymbol{S}}\left( t \right) + \mathit{\boldsymbol{n}}\left( t \right)} \right) =\\ \mathit{\boldsymbol{BS}}\left( t \right) + {\mathit{\boldsymbol{W}}^{ - 1}}{\mathit{\boldsymbol{G}}^{\rm{H}}}\mathit{\boldsymbol{n}}\left( t \right) = \mathit{\boldsymbol{BS}}\left( t \right) + \mathit{\boldsymbol{n'}}\left( t \right) $

(6)

式中：B=[b(θ₁), …, b(θ_K)]∈C^(M+N-1)×K具有范德蒙结构; n′(t)=W^-1G^Hn(t)为一个(M+N-1)×1的加性高斯噪声矢量。为表示方便，定义K维全一矢量η=[1, …, 1]∈C^1×K，则B可以表示为

$ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\eta }}\\ {\mathit{\boldsymbol{\eta \boldsymbol{\varPhi} }}}\\ \vdots \\ {\mathit{\boldsymbol{\eta }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{M + N - 2}}} \end{array}} \right] $

(7)

式中B的第i行为B_i=ηΦ^i-1, i=1, …, Μ+Ν-1。

2.2 前向空间平滑

以均匀的采样间隔采集J个快拍的信号并依次进行变换可得

$ \mathit{\boldsymbol{Y}} = \left[ {y\left( {{t_1}} \right),y\left( {{t_2}} \right), \cdots ,y\left( {{t_J}} \right)} \right] $

(8)

取前(J-1)和后(J-1)个快拍的信号，分别记为

$ {\mathit{\boldsymbol{Y}}_1} = \left[ {y\left( {{t_1}} \right),y\left( {{t_2}} \right), \cdots ,y\left( {{t_{J - 1}}} \right)} \right] = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{S}}_1} + {{\mathit{\boldsymbol{N'}}}_1} $

(9)

$ {\mathit{\boldsymbol{Y}}_2} = \left[ {y\left( {{t_2}} \right),y\left( {{t_3}} \right), \cdots ,y\left( {{t_J}} \right)} \right] = \mathit{\boldsymbol{B\psi }}{\mathit{\boldsymbol{S}}_1} + {{\mathit{\boldsymbol{N'}}}_2} $

(10)

式中

$ {\mathit{\boldsymbol{S}}_1} = \left[ {S\left( {{t_1}} \right),S\left( {{t_2}} \right), \cdots ,S\left( {{t_{J - 1}}} \right)} \right] $

$ {{\mathit{\boldsymbol{N'}}}_1} = \left[ {n'\left( {{t_1}} \right),n'\left( {{t_2}} \right), \cdots ,n'\left( {{t_{J - 1}}} \right)} \right] $

$ {{\mathit{\boldsymbol{N'}}}_2} = \left[ {n'\left( {{t_2}} \right),n'\left( {{t_3}} \right), \cdots ,n'\left( {{t_J}} \right)} \right] $

$ \mathit{\boldsymbol{\psi }} = {\rm{diag}}\left( {{{\rm{e}}^{{\rm{j2 \mathsf{ π} }}{f_{d1}}/{f_{\rm{s}}}}},{{\rm{e}}^{{\rm{j2 \mathsf{ π} }}{f_{d2}}/{f_{\rm{s}}}}}, \cdots ,{{\rm{e}}^{{\rm{j2 \mathsf{ π} }}{f_{dK}}/{f_{\rm{s}}}}}} \right) $

Y₁和Y₂可按如下形式分成(M+N-1)块

$ {\mathit{\boldsymbol{Y}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{1,1}}}\\ \vdots \\ {{\mathit{\boldsymbol{Y}}_{1,M + N - 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{1,1}}}\\ \vdots \\ {{\mathit{\boldsymbol{B}}_{M + N - 1}}} \end{array}} \right]{\mathit{\boldsymbol{S}}_1} + {{\mathit{\boldsymbol{N'}}}_1} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\eta }}\\ {\mathit{\boldsymbol{\eta \boldsymbol{\varPhi} }}}\\ \vdots \\ {\mathit{\boldsymbol{\eta }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{M + N - 2}}} \end{array}} \right]{\mathit{\boldsymbol{S}}_1} + {{\mathit{\boldsymbol{N'}}}_1} $

$ {\mathit{\boldsymbol{Y}}_2} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{2,1}}}\\ \vdots \\ {{\mathit{\boldsymbol{Y}}_{2,M + N - 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\left( {\mathit{\boldsymbol{B\psi }}} \right)}_1}}\\ \vdots \\ {{{\left( {\mathit{\boldsymbol{B\psi }}} \right)}_{M + N - 1}}} \end{array}} \right]{\mathit{\boldsymbol{S}}_1} + {{\mathit{\boldsymbol{N'}}}_2} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\eta \psi }}}\\ {\mathit{\boldsymbol{\eta \psi \boldsymbol{\varPhi} }}}\\ \vdots \\ {\mathit{\boldsymbol{\eta \psi }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{M + N - 2}}} \end{array}} \right]{\mathit{\boldsymbol{S}}_1} + {{\mathit{\boldsymbol{N'}}}_2} $

式中：Y₁和Y₂的第i行分别为Y_{1, i}=ηΦ^i-1S₁+N′_{1, i}和Y_{2, i}=ηψΦ^i-1S₁+N′_{2, i}; (Bψ)_i, N′_{1, i}和N′_{2, i}分别为Bψ，N′₁和N′₂的第i行。取B和BψZ的第i行构造矩阵B_{E, i}，由B和Bψ的范德蒙特性可得

$ {\mathit{\boldsymbol{B}}_{E,i}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_i}}\\ {{{\left( {\mathit{\boldsymbol{B\psi }}} \right)}_i}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\eta }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{i - 1}}}\\ {\mathit{\boldsymbol{\eta \psi }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{i - 1}}} \end{array}} \right] = {\mathit{\boldsymbol{B}}_{E,1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{i - 1}} \in {{\bf{C}}^{2 \times K}} $

(11)

式中B_{E, 1}=[η^T, ηψ^T]^T。

构造矩阵Y_E，其共分为(M+N-1)个子矩阵，其第i个子矩阵由Y₁和Y₂的第i行构成，Y_E可写成

$ {\mathit{\boldsymbol{Y}}_E} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{Y}}_{1,1}}}\\ {{\mathit{\boldsymbol{Y}}_{2,1}}}\\ {{\mathit{\boldsymbol{Y}}_{1,2}}}\\ {{\mathit{\boldsymbol{Y}}_{2,2}}}\\ \vdots \\ {{\mathit{\boldsymbol{Y}}_{1,M + N - 1}}}\\ {{\mathit{\boldsymbol{Y}}_{2,M + N - 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{E,1}}}\\ {{\mathit{\boldsymbol{B}}_{E,2}}}\\ \vdots \\ {{\mathit{\boldsymbol{B}}_{E,M + N - 1}}} \end{array}} \right]{\mathit{\boldsymbol{S}}_1} + {{\mathit{\boldsymbol{N'}}}_E} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{E,1}}}\\ {{\mathit{\boldsymbol{B}}_{E,1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}\\ \vdots \\ {{\mathit{\boldsymbol{B}}_{E,1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{M + N - 2}}} \end{array}} \right]{\mathit{\boldsymbol{S}}_1} + \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{N'}}}_{E,1}}}\\ {{{\mathit{\boldsymbol{N'}}}_{E,2}}}\\ \vdots \\ {{{\mathit{\boldsymbol{N'}}}_{E,M + N - 1}}} \end{array}} \right] $

(12)

式中：第i个子矩阵表示为Y_{E, i} =B_{E, 1}Φ^i-1S₁+N′_{E, i}∈C^2×Κ; N′_E和N′_{E, i}为相应的噪声矩阵。

前向平滑技术要求将Y_E的(M+N-1)个子矩阵分成P个充分的子矩阵序列。令L表示每个子矩阵序列包含的子矩阵数量，Y_{FSS, p}, p=1, 2, …, P表示第p个子矩阵序列。取第一个序列为参考，则这P个子矩阵序列可以表示为^[17]

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{Y}}_{{\rm{FSS}},1}} = {\left[ {{\mathit{\boldsymbol{Y}}_{E,1}}^{\rm{T}}, \cdots ,{\mathit{\boldsymbol{Y}}_{E,L}}^{\rm{T}}} \right]^{\rm{T}}}\\ {\mathit{\boldsymbol{Y}}_{{\rm{FSS}},2}} = {\left[ {{\mathit{\boldsymbol{Y}}_{E,2}}^{\rm{T}}, \cdots ,{\mathit{\boldsymbol{Y}}_{E,L + 1}}^{\rm{T}}} \right]^{\rm{T}}}\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \\ {\mathit{\boldsymbol{Y}}_{{\rm{FSS}},P}} = {\left[ {{\mathit{\boldsymbol{Y}}_{E,P}}^{\rm{T}}, \cdots ,{\mathit{\boldsymbol{Y}}_{E,M + {N_{ - 1}}}}^{\rm{T}}} \right]^{\rm{T}}} \end{array} \right. $

(13)

第p个序列可表示为Y_{FSS, p} = [Y_{E, p}^T, Y_{E, p + 1}^T , …, Y_{E, p + L-1}^T]^T = B_ELΦ^{p- 1}S₁ + N_L′，其中L=M+N-P，B_EL=[B_{E, 1}^T , (B_{E, 1}Φ)^T, …, (B_{E, 1}Φ^L-1)^T]^T; N′_L为相应的噪声矩阵。

第p个序列的协方差矩阵R_{RD, p}为

$ {\mathit{\boldsymbol{R}}_{{\rm{RD}},p}} = E\left[ {{\mathit{\boldsymbol{V}}_{{\rm{FSS}},p}}\mathit{\boldsymbol{V}}_{{\rm{FSS}},p}^{\rm{H}}} \right] = {\mathit{\boldsymbol{B}}_{EL}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{p - 1}}{\mathit{\boldsymbol{R}}_s}{\left( {{\mathit{\boldsymbol{B}}_{EL}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{p - 1}}} \right)^{\rm{H}}} + {\mathit{\boldsymbol{W}}^{ - 1}}{\sigma ^2}{\mathit{\boldsymbol{I}}_{2L}} $

计算所有P个序列的协方差并计算其平均值，即可得到经过前向平滑后的阵列协方差矩阵

$ {\mathit{\boldsymbol{R}}_{{\rm{RDf}}}} = \frac{1}{P}\sum\limits_{p = 1}^P {{\mathit{\boldsymbol{R}}_{{\rm{RD}},p}}} = {\mathit{\boldsymbol{B}}_{EL}}\left( {\frac{1}{P}\sum\limits_{p = 1}^P {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{p - 1}}{\mathit{\boldsymbol{R}}_s}{{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{p - 1}}} \right)}^{\rm{H}}}} } \right){\mathit{\boldsymbol{B}}_{EL}} + {\mathit{\boldsymbol{W}}^{ - 1}}{\sigma ^2}{\mathit{\boldsymbol{I}}_{2L}} = \\{\mathit{\boldsymbol{B}}_{EL}}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_{EL}^{\rm{H}} + {\mathit{\boldsymbol{W}}^{ - 1}}{\sigma ^2}{\mathit{\boldsymbol{I}}_{2L}} $

(14)

式中平滑后的信源协方差矩阵$\mathit{\boldsymbol{R}}_s^f = \frac{1}{P}\sum\limits_{p = 1}^P {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{p - 1}}{\mathit{\boldsymbol{R}}_s}{{\left( {{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{p - 1}}} \right)}^{\rm{H}}}} $满秩(详细证明见文献[17])。

2.3 基于PM算法的DOA和多普勒频率联合估计

将B_EL按如下形式分块^[13]

$ {\mathit{\boldsymbol{B}}_{EL}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{B}}_2}} \end{array}} \right] $

(15)

式中：B₁为一K×K的非奇异矩阵，B₂∈C^(2L-K)×K。B₂可被视作B₁的线性变换

$ \mathit{\boldsymbol{P}}_{{\rm{RDc}}}^{\rm{H}}{\mathit{\boldsymbol{B}}_1} = {\mathit{\boldsymbol{B}}_2} $

(16)

式中P_RDc∈C^K×(2L-K)为传播算子矩阵。经过前向平滑后的阵列协方差矩阵R_RDf可写作

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{\rm{RDf}}}} = {\mathit{\boldsymbol{B}}_{EL}}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_{EL}^{\rm{H}} + {\mathit{\boldsymbol{I}}_{2L}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{B}}_2}} \end{array}} \right]\mathit{\boldsymbol{R}}_s^f\left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{B}}_1^{\rm{H}}}&{\mathit{\boldsymbol{B}}_2^{\rm{H}}} \end{array}} \right] + {\mathit{\boldsymbol{I}}_{2L}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_1^{\rm{H}}}&{{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_2^{\rm{H}}}\\ {{\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_1^{\rm{H}}}&{{\mathit{\boldsymbol{B}}_2}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_2^{\rm{H}}} \end{array}} \right] }\\ {+ {\mathit{\boldsymbol{I}}_{2L}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_1^{\rm{H}}}&{{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_1^{\rm{H}}{\mathit{\boldsymbol{P}}_{{\rm{RDc}}}}}\\ {\mathit{\boldsymbol{P}}_{{\rm{RDc}}}^{\rm{H}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_1^{\rm{H}}}&{\mathit{\boldsymbol{P}}_{{\rm{RDc}}}^{\rm{H}}{\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{R}}_s^f\mathit{\boldsymbol{B}}_1^{\rm{H}}{\mathit{\boldsymbol{P}}_{{\rm{RDc}}}}} \end{array}} \right] + {\mathit{\boldsymbol{I}}_{2L}}} \end{array} $

(17)

取R_RDf的前K列，记为R_RDf1，剩下的(2L-K)列记为R_RDf2，则传播算子矩阵P_RDc可由R_RDf估计得到

$ {\mathit{\boldsymbol{P}}_{{\rm{RDc}}}} = \mathit{\boldsymbol{R}}_{{\rm{RDf1}}}^ + {\mathit{\boldsymbol{R}}_{{\rm{RDf2}}}} $

(18)

式中：R_RDf1∈C^2L×K，R_RDf2∈C^2L×(2L-K)。

定义P_RD=[I_K, P_RDc]^H，由式(15, 16)得

$ {\mathit{\boldsymbol{P}}_{{\rm{RD}}}}{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_1}}\\ {{\mathit{\boldsymbol{B}}_2}} \end{array}} \right] = {\mathit{\boldsymbol{B}}_{EL}} $

(19)

根据式(12)，将P_RD同样分成L个子矩阵

$ {\mathit{\boldsymbol{P}}_{{\rm{RD}}}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{{\rm{RD,1}}}}}\\ {{\mathit{\boldsymbol{P}}_{{\rm{RD,2}}}}}\\ \vdots \\ {{\mathit{\boldsymbol{P}}_{{\rm{RD,}}L}}} \end{array}} \right] $

(20)

式中P_{RD, i}∈C^2×K, i=1, 2, …, L。取P_RD的前(L-1)和后(L-1)个子矩阵，分别记为P_RD1和P_RD2，可得

$ {\mathit{\boldsymbol{P}}_{{\rm{RD1}}}}{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{E,1}}}\\ \vdots \\ {{\mathit{\boldsymbol{B}}_{E,1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{L - 2}}} \end{array}} \right] $

(21)

$ {\mathit{\boldsymbol{P}}_{{\rm{RD2}}}}{\mathit{\boldsymbol{B}}_1} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{B}}_{E,1}}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}}\\ \vdots \\ {{\mathit{\boldsymbol{B}}_{E,1}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{L - 1}}} \end{array}} \right] $

(22)

由式(21)和式(22)可得P_RD1B₁Φ=P_RD2B₁，也即

$ {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPhi} B}}_1^{ - 1} = \mathit{\boldsymbol{P}}_{{\rm{RD1}}}^ + {\mathit{\boldsymbol{P}}_{{\rm{RD2}}}} $

(23)

令φ=P_RD1⁺P_RD2。由式(23)可得φ和Φ是相似矩阵，有相同的特征值。对φ特征值分解，记其特征值为[λ₁, λ₂, …, λ_K]，${\mathit{\boldsymbol{\hat B}}_1}$为对应的特征矢量集合，${\mathit{\boldsymbol{\hat B}}_1}$即为B₁的估计，且${\mathit{\boldsymbol{\hat B}}_1}$=B₁Π，Π为列模糊矩阵，Π^-1=Π，所以Φ的估计为${\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}$= ΠΦΠ。由φ的特征值可得DOA的估计值为

$ {{\hat \theta }_k} = \arcsin \left( { - {\rm{angle}}\left( {{\lambda _k}} \right)\lambda /2{\rm{ \mathsf{ π} }}d} \right)\;\;\;\;k = 1,2, \cdots ,K $

(24)

将P_RD右乘$ \mathit{\boldsymbol{\hat B}}_1^{ - 1}$可得B_EL的估计${{\mathit{\boldsymbol{\hat B}}}_{EL}}$。由${{\mathit{\boldsymbol{\hat B}}}_{E, 1}} = {\left[{{{\mathit{\boldsymbol{\hat \eta }}}^{\rm{T}}}, {{\left( {\mathit{\boldsymbol{\hat \eta \hat \psi }}} \right)}^{\rm{T}}}} \right]^{\rm{T}}}$和B_{E, i}=B_{E, 1}Φ^i-1，将${{\mathit{\boldsymbol{\hat B}}}_{EL}}$进行行变换得到${{\mathit{\boldsymbol{\tilde B}}}_{EL}}$

$ {{\mathit{\boldsymbol{\tilde B}}}_{EL}} = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{\eta }}\\ \vdots \\ {\mathit{\boldsymbol{\eta }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{L - 1}}}\\ {\mathit{\boldsymbol{\eta \psi }}}\\ \vdots \\ {\mathit{\boldsymbol{\eta }}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{L - 1}}\mathit{\boldsymbol{\psi }}} \end{array}} \right]\mathit{\boldsymbol{ \boldsymbol{\varPi} }} = \left[ {\begin{array}{*{20}{c}} {{{\mathit{\boldsymbol{\tilde B}}}_{ELa}}}\\ {{{\mathit{\boldsymbol{\tilde B}}}_{ELb}}} \end{array}} \right] $

(25)

式中${{\mathit{\boldsymbol{\tilde B}}}_{ELa}} $和${{\mathit{\boldsymbol{\tilde B}}}_{ELb}} $分别包含了${{\mathit{\boldsymbol{\tilde B}}}_{EL}} $的前L行和后L行。随后可得Ψ的估计

$ \mathit{\boldsymbol{\hat \psi }} = \mathit{\boldsymbol{\tilde B}}_{ELa}^ + {{\mathit{\boldsymbol{\tilde B}}}_{ELb}} = \mathit{\boldsymbol{ \boldsymbol{\varPi} \psi \boldsymbol{\varPi} }} $

(26)

则多普勒频率估计为

$ \begin{array}{*{20}{c}} {{f_{{\rm{d}}k}} = {\rm{angle}}\left( {{\gamma _k}} \right){f_{\rm{s}}}/\left( {2{\rm{ \mathsf{ π} }}} \right)}&{k = 1,2, \cdots ,K} \end{array} $

(27)

式中γ_k为${\mathit{\boldsymbol{\hat \psi }}}$的第k个对角元素。

本算法中，由于${\mathit{\boldsymbol{ \boldsymbol{\hat \varPhi} }}}$和Ψ的估计过程中列模糊矩阵相同，因而本算法对于目标的DOA和多普勒频率两项参数的估计可以实现自动配对。

本文所提RD-FSS-PM的主要步骤及相应复杂度总结如下：

(1)按式(6)对接收信号进行降维变换得到Y，并继而得到Y_E…………………………无需复乘运算；

(2)按式(13，14)由前向空间平滑得到R_RDf………………………………………O{P(J-1)(2L)²};

(3) 按式(18)估计传播算子矩阵P_RDc，构造P_RD………………………O{4LK²+2LK(2L-K)+K³};

(4) 对P_RD分块，得到P_RD1和P_RD2，由旋转不变性，按式(23，24)估计DOA……O{6K²(L-1)+2K³};

(5) 构造${{\mathit{\boldsymbol{\tilde B}}}_{ELa}}$和${{\mathit{\boldsymbol{\tilde B}}}_{ELb}}$，由式(27)估计多普勒频率……………………………O{5K²L+K³)}。

3 算法分析 3.1 复杂度分析

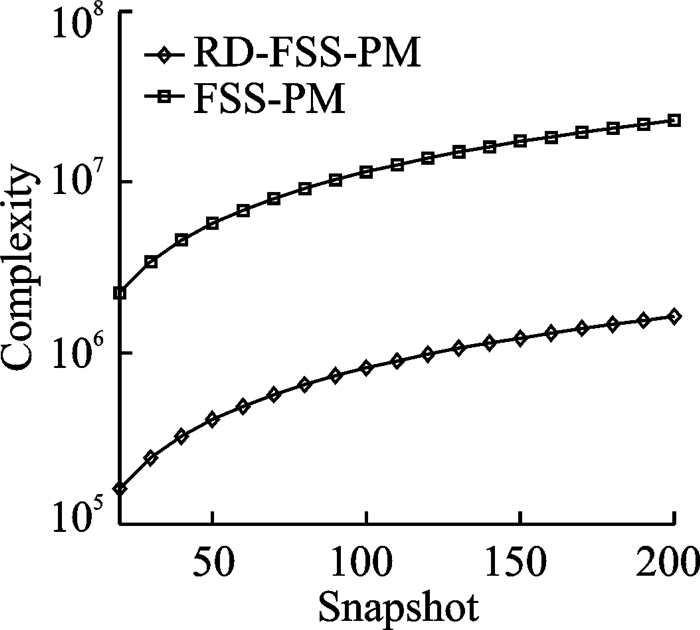
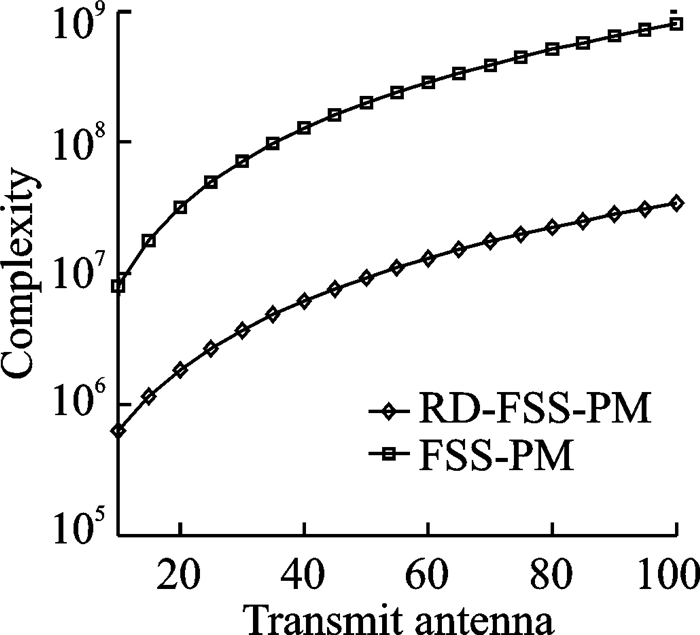
本算法所采用的降维变换可以有效降低复杂度。所提算法的复杂度为O{P(J-1)(2L)²+4L²K+13K²L-6K²+4K³}, P=M+N-L。与之对比，传统的FSS-PM算法需要O{(J-1)P(2LM)²+4L²M²K+13K²LM-6K²M+4K³}, P=N-L+1。图 2和图 3给出了RD-FSS-PM算法和传统FSS-PM算法的复杂度随快拍数和发射天线数的变化对比图。图 2中，M=12，N=12，K=3，P=8，快拍数由10增加到200。图 3中，N=12，K=3，P=8，J=100，发射天线数由10增加到100。由图 2和图 3可得，所提RD-FSS-PM算法相比FSS-PM算法，复杂度有明显降低。

3.2 误差分析

在噪声干扰下，实际协方差矩阵为

$ {{\mathit{\boldsymbol{\bar R}}}_{{\rm{RDf}}}} \buildrel \Delta \over = {\mathit{\boldsymbol{R}}_{{\rm{RDf}}}} + \partial {\mathit{\boldsymbol{R}}_{{\rm{RDf}}}} $

式中：R_RDf为真实值，∂R_RDf为误差矩阵。取R_RDf的前K行和后(2L-K)行，记为R_RDf1和R_RDf2，有

$ {{\mathit{\boldsymbol{\bar R}}}_{{\rm{RDf1}}}} \buildrel \Delta \over = {\mathit{\boldsymbol{R}}_{{\rm{RDf1}}}} + \partial {\mathit{\boldsymbol{R}}_{{\rm{RDf1}}}} $

$ {{\mathit{\boldsymbol{\bar R}}}_{{\rm{RDf2}}}} \buildrel \Delta \over = {\mathit{\boldsymbol{R}}_{{\rm{RDf2}}}} + \partial {\mathit{\boldsymbol{R}}_{{\rm{RDf2}}}} $

式中：∂R_RDf1和∂R_RDf2分别为R_RDf1和R_RDf2的误差。定义P_RDc$ \buildrel \Delta \over = $P_RDc+∂P_RDc，其中∂P_RDc为传播算子P_RDc的误差矩阵，且可由∂R_RDc^H=(R_RDf1^HR_RDf1)^-1R_RDf1^H(∂R_RDf2-∂R_RDf1R_RDc^H)估计得到。有噪情形下，P_RD可以表示为

$ {{\mathit{\boldsymbol{\bar P}}}_{{\rm{RD}}}} = \left[ \begin{array}{l} {\mathit{\boldsymbol{I}}_K}\\ {{\mathit{\boldsymbol{\bar P}}}_{{\rm{RDc}}}} \end{array} \right] = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{{\rm{RD}},1}} + \partial {\mathit{\boldsymbol{P}}_{{\rm{RD}},1}}}\\ {{\mathit{\boldsymbol{P}}_{{\rm{RD}},2}} + \partial {\mathit{\boldsymbol{P}}_{{\rm{RD}},2}}}\\ \vdots \\ {{\mathit{\boldsymbol{P}}_{{\rm{RD}},L}} + \partial {\mathit{\boldsymbol{P}}_{{\rm{RD}},L}}} \end{array}} \right] $

(28)

式中∂P_{RD, i}∈C^2×K为∂P_RD的第i个子矩阵。由(P_RD1+∂P_RD1)⁺的一阶近似，可得^[12]

$ \mathit{\boldsymbol{\hat \varphi }} = \mathit{\boldsymbol{B}}_1^{ - 1}\left( {{\mathit{\boldsymbol{I}}_K} + \mathit{\boldsymbol{P}}_{{\rm{RD1}}}^ + \left( {\partial {\mathit{\boldsymbol{P}}_{{\rm{RD}}2}} - \partial {\mathit{\boldsymbol{P}}_{{\rm{RD}}1}}} \right)} \right)\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{B}}_1} $

(29)

$ {\mathit{\boldsymbol{\hat \varphi }}}$的第k个特征值为λ_k=λ_k+∂λ_k，其中∂λ_k =∂λ_ke_k^TP_RD1⁺(∂P_RD2-∂P_RD1)e_k，e_k的第k个元素为1，其余元素为0。

根据$ {{\mathit{\boldsymbol{\hat B}}}_1} = {\mathit{\boldsymbol{B}}_1}\mathit{\boldsymbol{ \boldsymbol{\varPi} }}$，有

$ {{\mathit{\boldsymbol{\bar {\hat B}}}}_1} = {{\mathit{\boldsymbol{\hat B}}}_1} + \partial {{\mathit{\boldsymbol{\hat B}}}_1} $

(30)

式中$\partial {{\mathit{\boldsymbol{\hat B}}}_1}$为${{\mathit{\boldsymbol{\hat B}}}_1}$的误差。令P_RDo表示P_RD从第1行到第(2L-1)行中的奇数行，令P_RDe表示P_RD从第2行到第2L行中的偶数行。根据式(25，30)，有

$ {{\mathit{\boldsymbol{\bar {\tilde B}}}}_{Ela}} = {{\mathit{\boldsymbol{\bar P}}}_{{\rm{RDo}}}}{{\mathit{\boldsymbol{\bar {\hat B}}}}_1} = {\mathit{\boldsymbol{P}}_{{\rm{RDo}}}}{{\mathit{\boldsymbol{\hat B}}}_1} + {\mathit{\boldsymbol{P}}_{{\rm{RDo}}}}\partial {{\mathit{\boldsymbol{\hat B}}}_1} + \partial {\mathit{\boldsymbol{P}}_{{\rm{RDo}}}}{{\mathit{\boldsymbol{\hat B}}}_1} + \partial {\mathit{\boldsymbol{P}}_{{\rm{RDo}}}}\partial {{\mathit{\boldsymbol{\hat B}}}_1} $

$ {{\mathit{\boldsymbol{\bar {\tilde B}}}}_{Elb}} = {{\mathit{\boldsymbol{\bar P}}}_{{\rm{RDe}}}}{{\mathit{\boldsymbol{\bar {\hat B}}}}_2} = {\mathit{\boldsymbol{P}}_{{\rm{RDe}}}}{{\mathit{\boldsymbol{\hat B}}}_2} + {\mathit{\boldsymbol{P}}_{{\rm{RDe}}}}\partial {{\mathit{\boldsymbol{\hat B}}}_2} + \partial {\mathit{\boldsymbol{P}}_{{\rm{RDe}}}}{{\mathit{\boldsymbol{\hat B}}}_2} + \partial {\mathit{\boldsymbol{P}}_{{\rm{RDe}}}}\partial {{\mathit{\boldsymbol{\hat B}}}_2} $

根据${\left( {{{\mathit{\boldsymbol{\tilde B}}}_{ELa}} + \partial {{\mathit{\boldsymbol{\tilde B}}}_{ELa}}} \right)^ + }$的一阶近似，得到ψ的估计

$ \mathit{\boldsymbol{\hat \psi }} = \mathit{\boldsymbol{\psi }} + \mathit{\boldsymbol{\tilde B}}_{ELa}^ + \left( {\partial {{\mathit{\boldsymbol{\tilde B}}}_{ELb}} - \partial {{\mathit{\boldsymbol{\tilde B}}}_{ELa}}} \right)\mathit{\boldsymbol{\psi }} $

定义${{\hat\gamma}_k}={\gamma_k}+\partial{\gamma_k}$，其中γ_k和γ_k分别为ψ和$\mathit{\boldsymbol{\tilde B}}_{ELa}^+\left({\partial{{\mathit{\boldsymbol{\tilde B}}}_{ELb}}-\partial{{\mathit{\boldsymbol{\tilde B}}}_{ELa}}}\right)$ψ的第(k, k)个元素。

据此，可推导得DOA和多普勒频率估计的均方误差为

$ E\left\{ {{{\left( {\partial {\theta _i}} \right)}^2}} \right\} = {{\left( {\frac{\lambda }{{2{\rm{ \mathsf{ π} }}d\cos {\theta _i}}}} \right)}^2}{{\left[ {{\mathop{\rm Re}\nolimits} \left( {\frac{{\partial {\lambda _k}}}{{{\lambda _k}\left| {{\lambda _k}} \right|}}} \right)} \right]}^2} = \frac{1}{2}{{\left( {\frac{\lambda }{{2{\rm{ \mathsf{ π} }}d\cos {\theta _i}}}} \right)}^2}\left[ {E{{\left\{ {\left| {\frac{{\partial {\lambda _k}}}{{{\lambda _k}\left| {{\lambda _k}} \right|}}} \right|} \right\}}^2} - \\{\mathop{\rm Im}\nolimits} \left\{ {E{{\left\{ {\left| {\frac{{\partial {\lambda _k}}}{{{\lambda _k}\left| {{\lambda _k}} \right|}}} \right|} \right\}}^2}} \right\}} \right] = \frac{1}{2}{{\left( {\frac{\lambda }{{2{\rm{ \mathsf{ π} }}d}}} \right)}^2}{{\left[ {\frac{1}{{\cos {\theta _i}\sin {\theta _i}}}} \right]}^2} \cdot \left\{ {{{\left[ {\frac{\lambda }{{2{\rm{ \mathsf{ π} }}d\sin {\theta _i}}}} \right]}^2}E\left\{ {{{\left| {\partial {\lambda _k}} \right|}^2}} \right\} \\- {\mathop{\rm Im}\nolimits} \left\{ {E\left\{ {{{\left( {\lambda _k^ * } \right)}^2}{{\left( {\partial {\lambda _k}} \right)}^2}} \right\}} \right\}} \right\} $

(31)

$ E\left\{ {{{\left( {\Delta {f_i}} \right)}^2}} \right\} = {\left( {\frac{{{f_{\rm{s}}}}}{{2{\rm{ \mathsf{ π} }}{f_i}}}} \right)^2}{\left\{ {{\mathop{\rm Im}\nolimits} \left( {\frac{{\partial {\gamma _k}}}{{{\gamma _k}}}} \right)} \right\}^2} = \frac{1}{2}{\left( {\frac{{{f_{\rm{s}}}}}{{2{\rm{ \mathsf{ π} }}{f_i}}}} \right)^2}\left[ {E\left\{ {{{\left| {\partial {\gamma _k}} \right|}^2}} \right\} - {\mathop{\rm Re}\nolimits} \left\{ {E\left\{ {{{\left( {\partial {\gamma _k}} \right)}^2}{{\left( {\gamma _k^ * } \right)}^2}} \right\}} \right\}} \right] $

(32)

3.3 克拉美罗界(Cramer-Rao bound, CRB)

在估计理论中，CRB是无偏算法的理论性能上限，常作为衡量算法估计精度的基准。单基地MIMO雷达下角度和多普勒频率估计的CRB为^[25]

$ {\rm{CRB}} = \frac{{{\sigma ^2}}}{2}{\left( {{\mathop{\rm Re}\nolimits} \left( {{\mathit{\boldsymbol{D}}^{\rm{H}}}\mathit{\boldsymbol{D}}} \right)} \right)^{ - 1}} $

(33)

式中：σ²为噪声功率; D=[S^T⊗D₁, D₂⊗A], D₁= $\left[{\frac{{\partial {a_1}}}{{\partial {\theta _1}}}, \cdots, \frac{{\partial {a_K}}}{{\partial {\theta _K}}}} \right]$，D₂= $\left[{\frac{{\partial {s_1}}}{{\partial {f _1}}}, \cdots, \frac{{\partial {s_K}}}{{\partial {f _K}}}} \right]$。

3.4 算法优点

现将所提算法的优点总结如下：

(1) RD-FSS-PM算法适用于相干和非相干目标同时存在的场景，该性质在第2节算法推导和下一节仿真部分得到证实；

(2) RD-FSS-PM算法与FSS-PM算法相比复杂度大幅降低，该性质在3.1节复杂度分析部分得到证实；

(3) RD-FSS-PM算法对DOA估计精度与FSS-PM算法相比大幅改善，同时可保持相近的多普勒频率估计精度，该性质在下一节仿真部分得到证实；

(4) RD-FSS-PM算法可实现DOA和多普勒频率的自动配对，该性质在第2节算法推导部分得到证实。

4 仿真结果及分析

为检验所提算法的估计性能，使用蒙特卡洛仿真的方法进行比较各种算法的性能，并以均方根误差(Root mean squared error，RMSE)作为评价估计精度的量度

$ {\rm{RMSE}} = \frac{1}{K}\sum\limits_{k = 1}^K {\sqrt {\frac{1}{{3\;000}}\sum\limits_{l = 1}^{3\;000} {\left[ {{{\left( {{{\hat a}_{k,l}} - {a_k}} \right)}^2}} \right]} } } $

(34)

式中：${{\hat a}_{k, l}}$表示在第l次仿真中对第k个信源的DOA或多普勒频率的估计，l=1, …, 3 000, 所有仿真结果均基于3 000次蒙特卡洛仿真计算而得。仿真中假设单基地MIMO雷达收发两端均采用ULA阵列，d=λ/2，空间中存在K=3个远场目标，载频均为f_s=100 kHz，其DOA分别为θ₁=20°，θ₂=30°，θ₃=40°；多普勒频率分别为f₁=1 000 Hz，f₂=2 000 Hz，f₃=2 000 Hz，即目标2和目标3相干。定义信噪比为SNR=10log₁₀ $\left( {{{\left\| \mathit{\boldsymbol{X}} \right\|}^2}/{{\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{\tilde X}}} \right\|}^2}} \right)$。

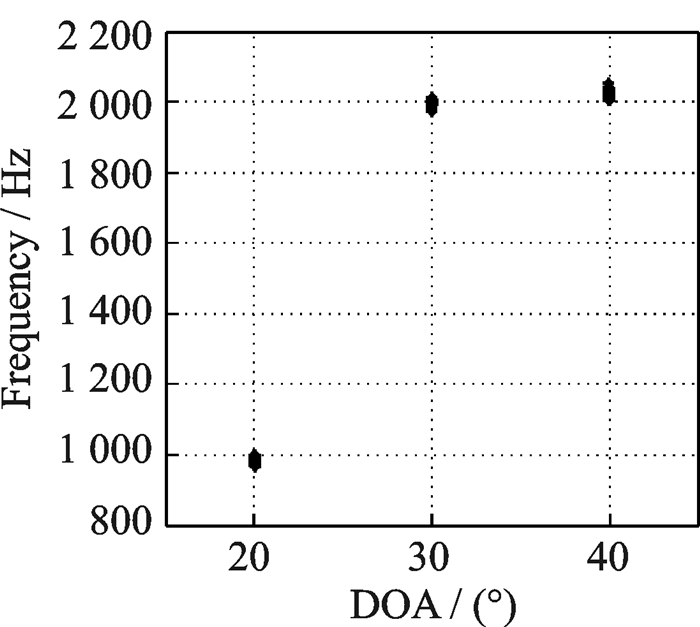
图 4显示了所提RD-FSS-PM算法在SNR=10 dB时的50次蒙特卡洛仿真的估计结果散布图，其余参数设置为M =12, N=12, J =100, P=8。由图 4可发现10 dB时，所提算法可精确估计，同时可实现DOA和多普勒频率的正确配对。

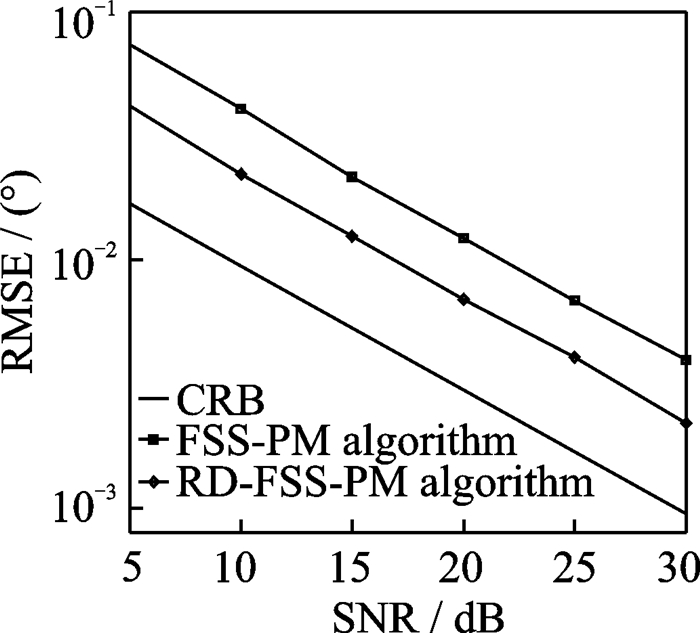
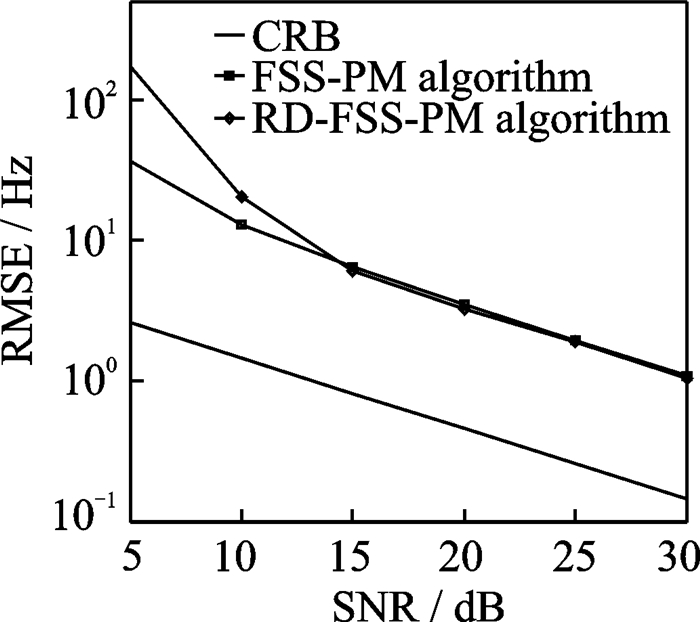
图 5, 6对所提RD-FSS-PM算法、传统FSS-PM算法的RMSE估计和CRB进行了对比。在图 5, 6中，假设M =12, N=12, J =100, P=10。由图 5, 6可发现，所提算法相比FSS-PM算法，DOA估计性能更接近CRB，准确度有明显提高，多普勒频率估计精度在较高信噪比下趋于接近。

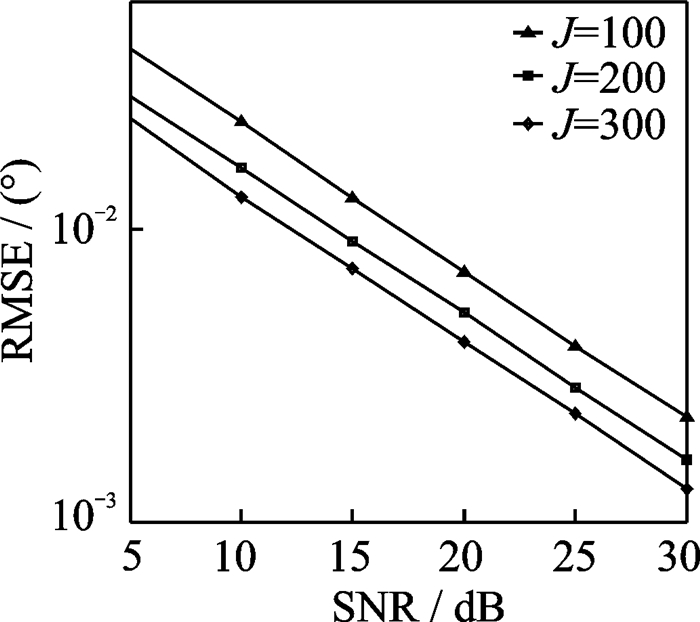
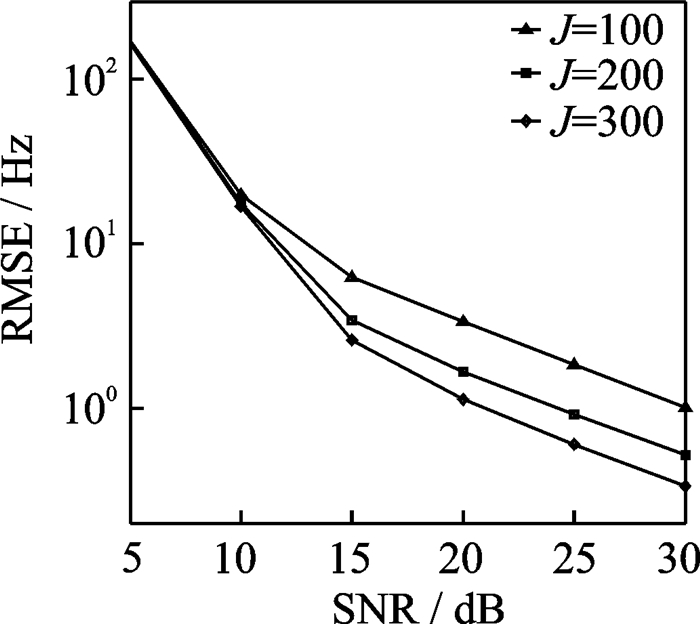
图 7, 8验证了所提RD-FSS-PM算法在不同快拍数情形下的性能并进行了对比。在图 7, 8中，假设快拍数分别为100，200，300，其余参数设置为M =12, N=12，P=8。由图 7, 8可得，快拍数增加时，其带来的可用信息也增多，所提算法的DOA估计精度得到提高。在低信噪比下，对多普勒频率的估计精度改善较小，随着信噪比增加，提升变得明显。

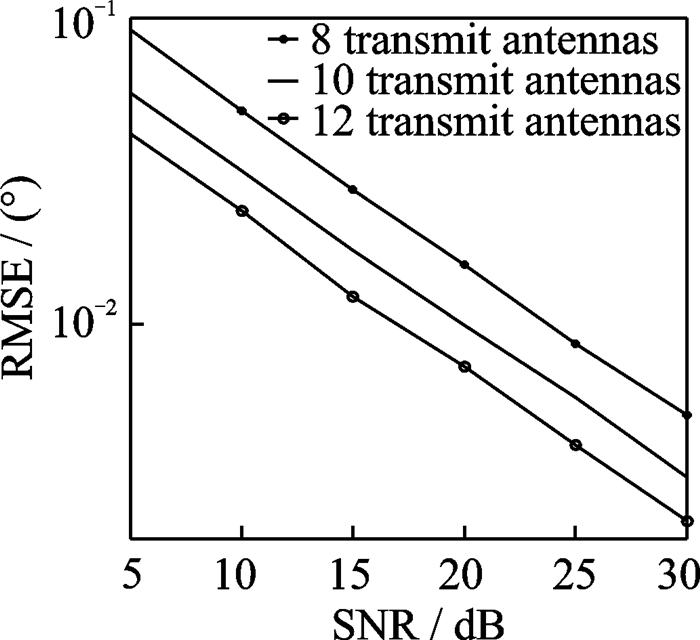
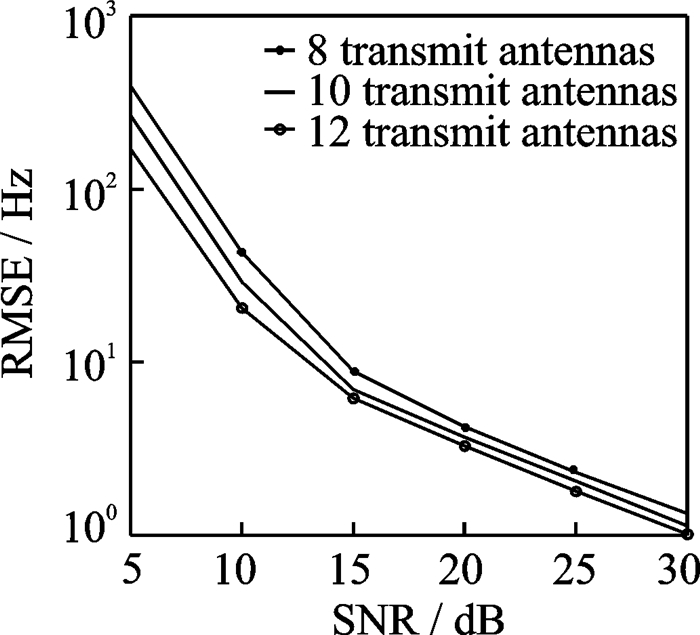
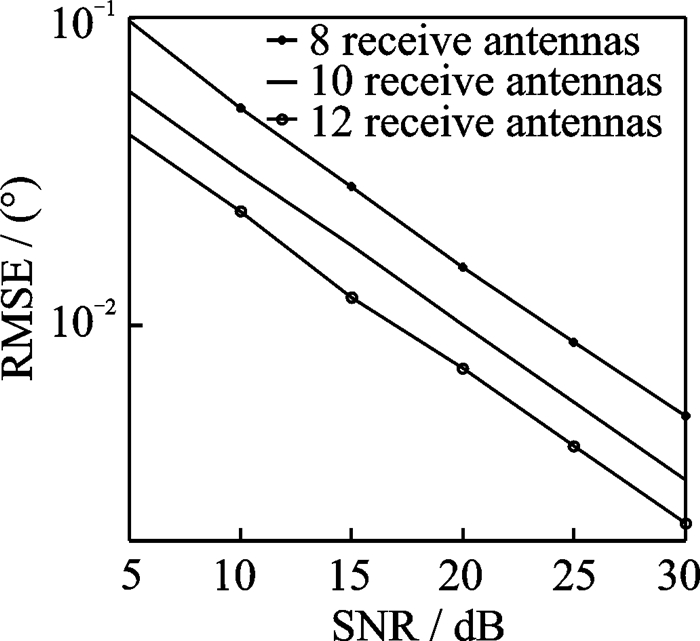
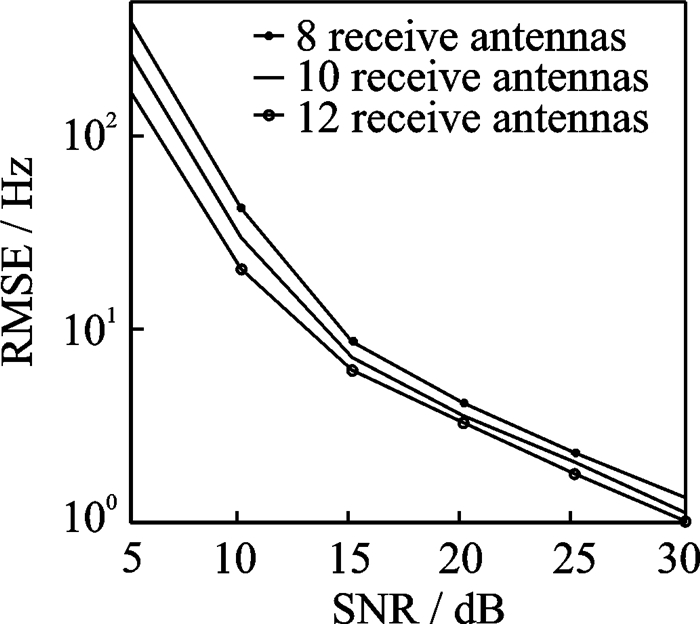
图 9-12分别显示了所提算法在发射、接收天线数变化时的DOA和多普勒频率估计性能。图 10, 11中，N=12, P=8，J=100，发射天线数为8, 10和12。图 12, 13中，M=12, P=8，J= 100，接收天线数为8, 10, 12。由图 9—12可得，由于分集增益的增加，所提算法在天线数增加时DOA和多普勒估计性能均得到改善。

5 结束语

针对单基地MIMO雷达下的DOA和多普勒频率联合估计问题，本文提出了一种基于降维变换的快速算法，并进行了复杂度和误差分析。所提RD-FSS-PM算法首先对接收信号进行降维变换，剔除冗余数据；随后应用前向空间平滑方法实现了对变换后的接收信号的解相干；最后依据旋转不变性，利用PM算法获得了对目标DOA和多普勒频率的估计。由仿真实验可知，所提RD-FSS-PM算法与传统FSS-PM算法相比，其复杂度大大降低，多普勒频率估计性能接近而DOA估计性能大为改善。