2. 东南大学信息科学与工程学院, 南京, 210096
2. School of Information Engineering, Southeast University, Nanjing, 210096, China
语音是人类社会信息重要的也是最便捷的载体。但是人类生存的环境却是一个极端复杂的声学环境,因此人类的通信通常会收到各种噪声的干扰。自然环境中的这些噪声严重影响了语音的质量和信息的传递。
语音增强技术旨在提升被噪声干扰语音的可懂度和质量。语音增强技术在助听器、耳蜗移植中广泛使用,语音增强技术的使用使得上述设备的听觉舒适度和可懂度得到提升。此外,在语音识别和说话人识别系统中,语音增强技术也有广泛的应用。
传统的单声道语音增强算法主要分为时域方法和频域方法。时域方法主要包括参数和滤波的方法等,而频域的方法有谱减法、维纳滤波法、听觉掩蔽法等[1]。其中谱减法是最简单,计算复杂度最小的方法,但会残留音乐噪声和严重的语音失真。而维纳滤波法能够将音乐噪声转变成白噪声,让处理后的语音听上去更舒适,但维纳滤波是基于平稳假设前提下的最小均方误差的估计,因此对非平稳信号的抑制能力较弱。听觉掩蔽法是根据人耳的掩蔽效应提出的一种算法。即能量大的声音会将能量小的声音掩蔽。此方法不用将噪声完全从语音中减去,只要将噪声能量抑制在掩蔽阈值以下。革命性的语音增强算法是1984年由Ephraim和Malah提出的基于最小均方误差(Minimum mean square error, MMSE)的语音幅度谱估计[2],由于人耳对声强的感知是非线性的,因而他们又提出了对数谱域的最小均方误差估计(LOG-MMSE)[3]。在LOG-MMSE语音增强方法提出的同时,Rainer Martin于1994年提出了基于最小统计量的语音增强方法[4],之后许多学者对此方法提出了相应改良,其中最重要的是Israel Cohen提出的最佳修正对数谱(Optimally-modified log-spectral amplitude, OM-LSA)语音增强算法[5]。此方法具有估计误差更小,对非平稳噪声跟踪的比较快的特点,可以认为LOG-MMSE和OM-LSA是目前传统单声道语音增强最优的算法。
传统语音增强算法可归结为无监督语音增强算法。随着深度学习概念的提出,语音增强算法迎来了新发展,即基于深度神经网络的语音增强方法, 例如, 在深度神经网络(Deep neural network, DNN)和卷积神经网络(Convolutional neural network, CNN)的基础上,设计了多种语音增强方案,其中经典的有理想二值掩蔽(Ideal binary masking, IBM)算法以及基于IBM的多值掩蔽方法等[6-9]。此外,生成对抗网络(Generative adversarial nets, GAN)[10]和长短时记忆网络(Long-short term memory, LSTM)[11]也被使用在语音增强领域中。
本文研究了将深度置信网络(Deep belief network, DBN)[12-14]应用于语音增强系统。主要思想是使用带噪语音的log谱和纯净语音的log谱对DBN进行训练,再把训练得到模型设计成一个非线性滤波器,对带噪语音进行滤波,而将带噪语音映射到纯净语音。不对语音和噪声的稳定性以及相互独立性做任何假设,可较好地应对非平稳环境[15]。
1 基于深度置信网络的语音增强算法及改进 1.1 基于受限玻尔兹曼机的DBN网络受限玻尔兹曼机(Restricted Boltzmann machines,RBM),以及由其构成的深度信念网络DBN,属于混合深度结构, 其作用是对数据进行预训练。RBM可以视为一种马尔可夫随机场(Markov random filed, MRF), 其通常功能是对数据进行编码后将编码数据交给监督学习方法去进行分类等操作,也就是将显层维度降维至隐层维度。而本文利用的功能则是通过RBM的训练得到RBM的权重矩阵和偏移量用来对训练样本进行初始化训练。事实证明,将训练后的权重和偏置直接作为神经网络的初始参数,而不是简单的产生高斯分布的随机数,可以非常好地避免陷入局部最优困境。
RBM模型实际是一种能量模型。能量函数最初是使用在热力学里面,用于描述系统的能量值,系统达到稳定状态的时候与能量最小的时候相对应。神经网络使用RBM时首次使用了能量函数。一个RBM中,显层中的所有可见单元以向量v来代表,隐层中的所有隐单元以向量h表示,设RBM的参数(权重wij,隐单元偏置aj,显单元偏置bi)为θ。则RBM的能量可以表示为
| $ E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right) = - \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{w_{ij}}{v_i}{h_j}} } - \sum\limits_{i = 1}^I {{b_i}{v_i}} - \sum\limits_{j = 1}^J {{a_j}{h_j}} $ | (1) |
写成矩阵形式为
| $ \mathit{\boldsymbol{E}} = - {\mathit{\boldsymbol{v}}^{\rm{T}}} \cdot \mathit{\boldsymbol{W}} \cdot \mathit{\boldsymbol{h}} - {\mathit{\boldsymbol{b}}^{\rm{T}}} \cdot \mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{a}}^{\rm{T}}} \cdot \mathit{\boldsymbol{h}} $ | (2) |
需要注意的是,上述能量函数的定义是针对于显层和隐层均为“伯努利分布-伯努利分布”的RBM,对于“高斯分布-伯努利分布”的RBM后面会谈到。RBM的向量v、向量h以及模型参数θ的联合概率P(v, h; θ)可以与能量函数E(v, h; θ)建立关系,即
| $ P\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right) = \frac{{{{\rm{e}}^{ - E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)}}}}{z} $ | (3) |
式中z为归一化因子,即
利用概率论知识,可以对P(v, h; θ)这个离散概率求出某一变量的边缘概率。由于实际上,通过显层输入数据(只考虑一个RBM情况下),而隐层则不能看到,本研究更加关注显层和模型参数的联合概率,或者看做是v的边缘概率,即更加关注
| $ P\left( {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right) = \sum\limits_\mathit{\boldsymbol{h}} {\frac{{{{\rm{e}}^{ - E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)}}}}{z}} $ | (4) |
考虑伯努利分布,一个单元(不论显单元还是隐单元),其输出为1则表示被激活,为0则未激活。利用贝叶斯公式和条件概率,可以求得
| $ \begin{array}{l} p\left( {{h_j} = 1\left| {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right.} \right) = {\rm{sigmod}}\left( {\sum\limits_{i = 1}^I {{w_{ij}}{v_i} + {a_j}} } \right);p\left( {{h_j} = 0\left| {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right.} \right) = 1 - {\rm{sigmod}}\left( {\sum\limits_{i = 1}^I {{w_{ij}}{v_i} + {a_j}} } \right)\\ p\left( {{v_i} = 1\left| {\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right.} \right) = {\rm{sigmod}}\left( {\sum\limits_{j = 1}^J {{w_{ij}}{h_j} + {b_i}} } \right);p\left( {{v_i} = 0\left| {\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right.} \right) = 1 - {\rm{sigmod}}\left( {\sum\limits_{j = 1}^J {{w_{ij}}{h_j} + {b_i}} } \right) \end{array} $ | (5) |
考虑上述的“伯努利分布-伯努利分布”中,每一层输出应为0或1,但是实际上第一层显层作为输入层时,往往输入是一个负无穷到正无穷之间的常数。这个时候我们需要引入一个高斯分布(可见单元分布)-伯努利分布(隐单元分布)的RBM,从而使输入层(显层)合理转化为隐层的0-1输出。对于这个高斯分布(可见单元分布)-伯努利分布(隐单元分布)的RBM,其能量函数为
| $ E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right) = - \sum\limits_{i = 1}^I {\sum\limits_{j = 1}^J {{w_{ij}}{v_i}{h_j}} } - \frac{1}{2}\sum\limits_{i = 1}^I {{{\left( {{v_i} - {b_i}} \right)}^2}} - \sum\limits_{j = 1}^J {{a_j}{h_j}} $ | (6) |
对应该类型RBM,前文所述的P(v, h; θ)与这里的联合概率形式上没有任何变化,只是E(v, h; θ)发生了改变。相应的,其条件概率改变为
| $ \begin{array}{*{20}{c}} {p\left( {{h_j} = 1\left| {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right.} \right) = {\rm{sigmod}}\left( {\sum\limits_{i = 1}^I {{w_{ij}}{v_i} + {a_j}} } \right);p\left( {{h_j} = 0\left| {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right.} \right) = 1 - {\rm{sigmod}}\left( {\sum\limits_{i = 1}^I {{w_{ij}}{v_i} + {a_j}} } \right)}\\ {p\left( {{v_i};\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right) = N\left( {\sum\limits_{j = 1}^J {{w_{ij}}{h_j}} + {b_i},1} \right)} \end{array} $ | (7) |
式中,vi为一个实际常数,sigmod函数定义不变,p(vi; h; θ)为一正态分布,其满足均值为
从之前的推导可以看出,P(v; θ)和能量函数有直接联系。能量函数越小,则P(v; θ)越高。考虑每次以
| $ \frac{{\partial \left( {\log P\left( {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right)} \right)}}{{\partial \mathit{\boldsymbol{\theta }}}} = \sum\limits_\mathit{\boldsymbol{h}} {\sum\limits_\mathit{\boldsymbol{v}} {P\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)\frac{{\partial \left( {E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)} \right)}}{{\partial \mathit{\boldsymbol{\theta }}}}} } - \sum\limits_\mathit{\boldsymbol{h}} {P\left( {\mathit{\boldsymbol{hv}};\mathit{\boldsymbol{\theta }}} \right)\frac{{\partial \left( {E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)} \right)}}{{\partial \mathit{\boldsymbol{\theta }}}}} $ | (8) |
即
| $ \begin{array}{l} {\left\langle {\frac{{\partial \left( {E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)} \right)}}{{\partial \mathit{\boldsymbol{\theta }}}}} \right\rangle _{P\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)}} = \sum\limits_\mathit{\boldsymbol{h}} {\sum\limits_\mathit{\boldsymbol{v}} {P\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)\frac{{\partial \left( {E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)} \right)}}{{\partial \mathit{\boldsymbol{\theta }}}}} } \\ {\left\langle {\frac{{\partial \left( {E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)} \right)}}{{\partial \mathit{\boldsymbol{\theta }}}}} \right\rangle _{P\left( {\mathit{\boldsymbol{h}}\left| {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right.} \right)}} = \sum\limits_\mathit{\boldsymbol{h}} {P\left( {\mathit{\boldsymbol{h}}\left| {\mathit{\boldsymbol{v}};\mathit{\boldsymbol{\theta }}} \right.} \right)\frac{{\partial \left( {E\left( {\mathit{\boldsymbol{v}},\mathit{\boldsymbol{h}};\mathit{\boldsymbol{\theta }}} \right)} \right)}}{{\partial \mathit{\boldsymbol{\theta }}}}} \end{array} $ | (9) |
多个RBM组合以产生的网络就称为深度信念网(DBN)。首先需要将数目一定的RBM堆叠在一起,然后进行预训练,预训练是从下往上进行训练。但是通常情况下,第一个RBM输入的值,即第一个RBM的显层并不是0或1,而是负无穷到正无穷的实值随机变量,例如某些连续特征。考虑先使用一个高斯-伯努利分布的RBM对训练数据进行训练,从而将该实值随机变量转化为二进制的数据,然后将该RBM的隐层作为下一个伯努利-伯努利分布的RBM的显层。
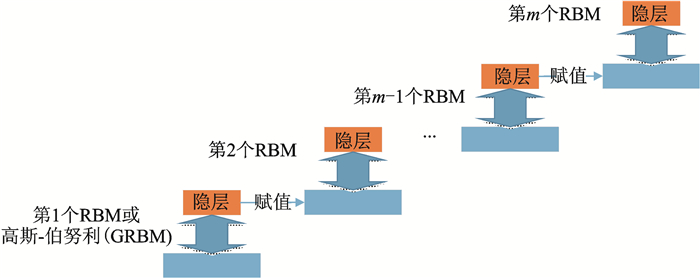
在上述RBM堆叠的过程中,由于不需要标签进行分类或判决,而只是一个非监督学习的生成模型,其实际上是提高了构建模型(即普通的DNN)在对数据进行训练时候的似然概率的变分下线,也就是使DBN最后的效果和最大近似似然学习相接近。当实际将DBN用来做分类等任务的时候(见图 1),上述预训练(或生成式预训练)一般需要和其他算法进行结合,例如该生成式预训练通常和判别式方法(有效的调整权重偏置等来改善网络进行判断的优良性)相结合,即通过判别式进行“精调”。
|
图 1 DBN模型 Fig. 1 DBN model |
1.2 基于深度置信网络的语音增强算法
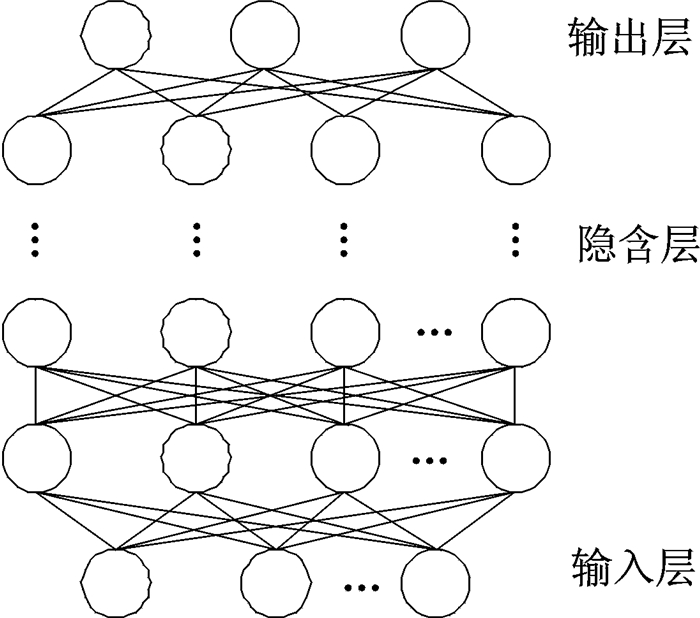
使用人工神经网络进行语音增强的主要思想是:使用语音信号训练人工神经网络,最终使网络具有去除噪声的能力[10],此算法使用到的语音库有带噪声的语音库和对应的纯净语音库[13]。2006年,Hinton提出了深度置信网络以及贪婪的逐层无监督训练算法,很好地解决了深层神经网络训练过程中出现的局部最优和过拟合问题[16]。由此,深度神经网络的概念就被提了出来,其结构图如图 2所示。
|
图 2 深度神经网络原理图 Fig. 2 Schematic diagram of deep neural network |
该结构图由输入层v、多个隐含层hk和输出层组成。只有相邻层节点之间有连接,同一层的节点之间无连接,每个连接都有一个权重值ω。
整个深度神经网络的训练主要由无监督和有监督训练组成。其训练过程为先用带噪语音的对数功率谱数据尝试训练一个深层的基于受限玻尔兹曼机的生成型模型。经过逐层贪婪式训练得到初始化网络参数之后,基于干净语音的对数功率谱特征和增强语音的对数功率谱特征之间的最小均方误差准则的反向错误传播算法来更新整个DNN的参数[15]。
对数功率谱特征的提取:首先对信号进行分帧,帧重叠为1/2。然后短时傅里叶变换被用在信号上进行DFT系数的计算,如下[10]
| $ \begin{array}{*{20}{c}} {Y\left( d \right) = \sum\limits_l^{L - 1} {y\left( l \right)h\left( l \right){{\rm{e}}^{ - {\rm{j2 \mathsf{ π} }}dl/L}}} }&{d = 0,1, \cdots ,L - 1} \end{array} $ | (10) |
式中d是频率维度,h(l)表示窗函数,若离散傅里叶变换的点数L如果能增加,即采样的信息点数更多,那么输入的特征将包含更多的信息。对数功率谱可定义为
| $ \begin{array}{*{20}{c}} {Y\left( d \right) = \log {{\left| {Y\left( d \right)} \right|}^2}}&{d = 0,1, \cdots ,D - 1} \end{array} $ | (11) |
式中D=L/2+1, 而对于d=D, …, L-1, Y(d)可通过对称准则获得,Y(d)=Y(L-d)。
波形重构:利用训练好的DBN估计得到感觉语音的对数功率谱特征之后,根据式(12)对波形进行重构[12]
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( d \right) = \exp \left\{ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( d \right)/2} \right\}\exp \left\{ {{\rm{j}}\angle Y\left( d \right)} \right\} $ | (12) |
式中相位信息∠Y(d)是取自原始带噪信号中的,这是因为人耳对相位的微小变化不敏感。
然后时域波形
| $ \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over x} \left( l \right) = \frac{1}{L}\sum {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over X} \left( k \right){{\rm{e}}^{ - {\rm{j2 \mathsf{ π} }}kl/L}}} $ | (13) |
整个句子的波形可以通过经典的重叠相加算法进行合成。
以上是基于深度置信网络语音增强算法的基线系统。基于基线系统训练出来的语音增强模型已经能较好地对大多场景下的带噪语音有较好的噪声抑制效果。但由于自然界中噪声的环境极其复杂多变,虽然本方案中采用了100种噪声作为训练噪声,但其远远达不到自然界中噪声种类的千万分之一。另外,基线系统损失函数将每个频点对损失函数贡献看做是一样的,而实际情况并非如此。针对以上问题,做出以下两点改进:
(1) 对噪声训练集加入频谱扰动,以丰富噪声频谱特性。
(2) 基于先验信噪比设计损失函数的权重因子,将不同频率点对损失函数的“贡献”加权。
1.3 噪声频率扰动通过以不同的信噪比将纯净语音和噪声混合的方式构造训练集,使用了大量的噪声种类来构造训练数据集,显著提高了模型的泛化能力。但噪声的种类虽然丰富,在实际场景中还存在许多非平稳的噪声,而训练集中噪声的种类仍然有限,且一些噪声的特性相似。因此,在有限的噪声样本里需要构造更多不同特性的噪声。
文献[17]的研究表明,在语音识别系统的训练样本中进行语音扰动,能够提升自动语音识别系统的识别性能,在本文的语音增强任务中,将噪声当做语音信号看待,对噪声信号进行扰动,以丰富噪声的特性。
所谓频率扰动就是将语谱中的频带随机上下移动。这里将频率扰动应用到噪声样本。频率扰动分为3个步骤[18]:
(1) 随机对每个时频单元r(f, t)赋值,这里取值服从-1到1的均匀分布,即
| $ r\left( {f,t} \right) \sim U\left( { - 1,1} \right) $ | (14) |
(2) 求相邻被赋值时频单元的平均值,得到扰动系数δ(f, t),求相邻时频单元均值的目的是为了防止过渡波动。表达式如下
| $ \delta \left( {f,t} \right) = \frac{\lambda }{{\left( {2p + 1} \right)\left( {2q + 1} \right)}}\sum\limits_{f' = f - p}^{f + p} {\sum\limits_{t' = t - q}^{t + q} {r\left( {f',t'} \right)} } $ | (15) |
式中p和q的取值决定了扰动的平滑性,λ决定扰动的程度。这3个值根据实际情况选取。
(3) 对语谱进行扰动处理
| $ \tilde S\left( {f,t} \right) = S\left( {f + \delta \left( {f,t} \right),t} \right) $ | (16) |
实际情况中,带噪语音不同频率点处的信号对误差函数的影响是不同的,而上文中的代价函数将所有的频点对误差的影响均看成一样的。
然而,在带噪语音信号中,不同频率段的信噪比其实是不一样的,信噪比高的部分语音被干扰小,因此不同频点对误差函数的“贡献”是有差别的[18]。因此,这里在损失函数中加入一个权重因子,来权衡不同频点对于误差产生的比重。表达式如下
| $ J\left( {\mathit{\boldsymbol{W}},\mathit{\boldsymbol{b}}} \right) = \frac{1}{D}\sum\limits_{\lambda = 0}^{\lambda = D - 1} {\sum\limits_{k = 0}^{k = N - 1} {\left\| {w_{\left( k \right)}^{\left( \lambda \right)} \cdot \left( {\hat X_{\left( k \right)}^{\left( \lambda \right)}\left( {{\mathit{\boldsymbol{W}}^\mathit{\boldsymbol{l}}},{\mathit{\boldsymbol{b}}^l}} \right) - X_{\left( k \right)}^{\left( \lambda \right)}} \right)} \right\|_2^2} } + \frac{{\tilde \omega }}{2}\left\| \mathit{\boldsymbol{W}} \right\|_2^2 $ | (17) |
式中w(k)(λ)>0表示第λ帧第k个频点的比重,称为频率权重系数。这里使用绝对听域AHT(fq)kλ来定义频率权重系数,满足频率权重系数跟绝对听阈变化趋势相反,选用公式如下
| $ w_{\left( k \right)}^{\left( \lambda \right)} = \alpha + \frac{\beta }{{1 + \exp \left[ {\frac{{{\rm{ATH}}\left( {{f_q}} \right)_k^\lambda }}{{20}}} \right]}} $ | (18) |
式中α>0决定了v(k)(λ)的下限,β>1决定了v(k)(λ)的变化幅度。这里α取0.5,β取2。频点fq绝对听阈的表达式为
| $ {\rm{ATH}}\left( {{f_q}} \right) = 3.64{\left( {\frac{{{f_q}}}{{1\;000}}} \right)^{ - 0.8}} - 6.5{\exp ^{\left[ { - 0.6{{\left( {\frac{{{f_q}}}{{1\;000}} - 3.3} \right)}^2}} \right]}} + {10^{ - 3}}{\left( {\frac{{{f_q}}}{{1\;000}}} \right)^4} $ | (19) |
本次实验的wav文件采样率为16 kHz。在对DBN训练的数据是来于TIMIT语音数据集构建的。噪声集是由汪德亮实验室公开的100种噪声。实验将TIMIT训练集里的4 620句感觉语音被用来和噪声相加在一起,相加的信噪比有20,15,10,5,0和-5 dB,来构建了近100 h的带噪数据(包含一小部分纯净语音的数据),来训练基于DNN的语音增强模型。而DBN网络结构为,1个输入层,1个输出层和3个隐层[9],输入层包含2 048个节点,隐层包含节点数为2 048。输入上下文的帧数为11帧,输出1帧数据。测试数据为从TIMIT测试集中随机挑选的200句和Pocketsphinx工程中给出的5条测试语音和5种未用于训练的噪声加在一起,构成带噪的测试集, 分别用本文提到的3种语音增强方案进行处理。
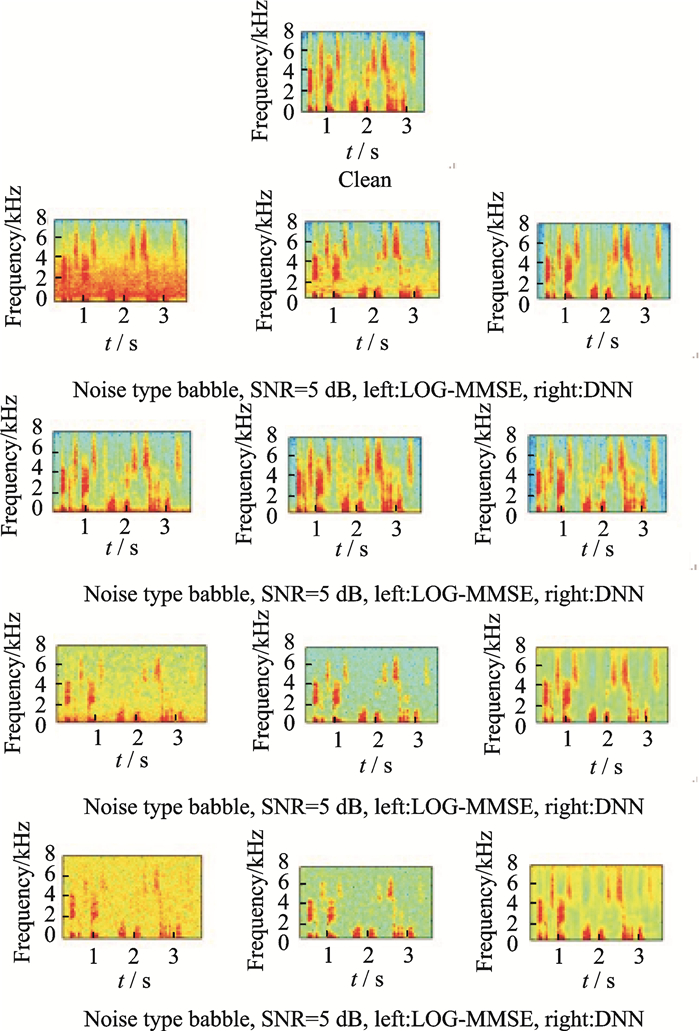
2.2 实验结果和分析 2.2.1 带噪语音经过不同算法处理结果语谱图对比图 3是测试了信噪比为5 dB时,算法在4种噪声情况下的性能。图 3的“clean”为纯净语音语谱图。以下按照四行三列的图描述。第1行为纯净语音分别加入白噪声、人声、汽车内噪声和粉红噪声的语谱图,第2列和第3列分别是对应带噪语音经过LOG-MMSE和DNN语音增强处理后的语谱图。
|
图 3 输入信噪比为5 dB时,不同噪声条件下两种算法性能语谱图对比 Fig. 3 Comparison of the spectrogramperformance of two algorithms under different noise conditions when SNR is 5 dB |
分析语谱图可以看出,在相同的输入条件下,LOG-MMSE对噪声有明显的抑制效果,同时,DNN在此条件下噪声的抑制效果从语谱图上看,比LOG-MMSE要好一些。再从语谱图细节上分析,比如,Speech babble噪声,两种算法处理的结果中可以看出,在2 000~4 000 Hz的区域,LOG-MMSE处理出来的语谱图有明显的模糊,而基于DNN的语音增强算法在这部分的语谱图脉络十分清晰。再对比其他噪声的处理结果,也能轻易发现,基于DNN的语音增强算法相比于LOG-MMSE算法能更好地保留语音中的成分。
2.2.2 带噪语音经过不同算法处理结果信噪比对比在白噪声、粉红噪声、嘈杂声和车内噪声环境下,对数域MMSE幅度估计器和深度神经网络在不同信噪比情况下对语音信噪比提升进行对比, 如表 1所示。
| 表 1 不同噪声环境下信噪比提升 Tab. 1 SNR improvement in different noise environments |
从表 1的信噪比数据的对比中可以看出,LOG-MMSE和基于DNN的语音增强算法能够有效地提升带噪语音信号的信噪比,而基于DNN的语音增强算法对带噪语音的信噪比提升更明显。
2.2.3 带噪语音经过不同算法处理结果客观语音质量评估(Perceptual evaluation of speech quality, PESQ)对比在白噪声、粉红噪声、嘈杂声和车内噪声环境下,对数域MMSE幅度估计器和深度神经网络在不同信噪比情况下对语音PESQ提升进行对比, 如表 2所示。
| 表 2 不同噪声环境下PESQ提升 Tab. 2 PESQ improvement in different noise environments |
同样,从表 2中的数据可以看出,LOG-MMSE和基于DNN的语音增强算法对带噪语音的PESQ也有不同程度的提升,其中DNN对带噪语音的PESQ提升要明显高于LOG-MMSE的提升。
3 结束语本文研究了基于深度置信网络的语音增强算法的基线系统,并对基线系统存在的不足做出了改进,在训练集引入噪声频谱扰动,同时根据先验信噪比构造损失函数权重因子,对损失函数进行改进。最后,为了验证本文改进的有效性,将本文改进算法与LOG-MMSE算法的性能从语谱图、信噪比和PESQ三方面进行对比,实验结果证明DBN语音增强方法具有较好的语音降噪效果,且增强后的语音质量更好。
| [1] |
Mowlaee P, Kulmer J. Phase estimation in single-channel speech enhancement:limits-potential[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2015, 23(8): 1283-1294. |
| [2] |
Ephraim Y, Malah D. Speech enhancement using a minimum-mean square error short-time spectral amplitude estimator[J]. Acoustics Speech & Signal Processing IEEE Transactions on, 2003, 32(6): 1109-1121. |
| [3] |
Ephraim Y, Malah D. Speech enhancement using a minimum mean-square error log-spectral amplitude estimator[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1985, 33(2): 443-445. |
| [4] |
Martin R. Noise power spectral density estimation based on optimal smoothing and minimum statistics[J]. IEEE Transactions on Speech and Audio Processing, 2001, 9(5): 504-512. DOI:10.1109/89.928915 |
| [5] |
Cohen I, Berdugo B. Speech enhancement for non-stationary noise environments[J]. Signal Processing, 2001, 81(11): 2403-2418. DOI:10.1016/S0165-1684(01)00128-1 |
| [6] |
Allen J. Short term spectral analysis, synthesis, and modification by discrete Fourier transform[J]. IEEE Transactions on Acoustics Speech & Signal Processing, 1977, 25(3): 235-238. |
| [7] |
Han K, Wang D L. Neural network based pitch tracking in very noisy speech[J]. Audio Speech & Language Processing IEEE/ACM Transactions on, 2014, 22(12): 2158-2168. |
| [8] |
Chen J, Wang Y, Wang D L. A feature study for classification-based speech separation at low signal-to-noise ratios[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2014, 22(12): 1993-2002. |
| [9] |
Zhang X L, Wang D L. Boosting contextual information for deep neural network based voice activity detection[J]. IEEE Press, 2016, 24(2): 252-264. |
| [10] |
Xu Y, Du J, Dai L R, et al. An experimental study on speech enhancement based on deep neural networks[J]. IEEE Signal Processing Letters, 2014, 21(1): 65-68. DOI:10.1109/LSP.2013.2291240 |
| [11] |
Healy E W, Yoho S E, Wang Y, et al. An algorithm to improve speech recognition in noise for hearing-impaired listeners:Consonant identification and articulatory feature transmission[J]. Journal of the Acoustical Society of America, 2013, 134(4): 3029-3034. DOI:10.1121/1.4820893 |
| [12] |
Hinton G E, Osindero S, Teh Y W. A fast learning algorithm for deep belief nets[J]. Neural Computation, 2006, 18(7): 15-27. |
| [13] |
Xu Y, Du J, Dai L R, et al. A regression approach to speech enhancement based on deep neural networks[J]. Audio Speech & Language Processing IEEE/ACM Transactions on, 2015, 23(1): 7-19. |
| [14] |
Xu Y, Du J, Huang Z, et al. Multi-objective learning and mask-based post-processing for deep neural network based speech enhancement[EB/OL].(2017-3-21)[2018-01-20].http://cn.arxiv.org/abs/1703.07172.
|
| [15] |
Xu Yong, Du Jun, Dai Lirong, et al. A regression approach to speech enhancement based on deep neural networks[J]. IEEE/ACM Transactions on Audio Speech & Language Processing, 2015, 23(1): 7-19. |
| [16] |
Hinton G E. A practical guide to training restricted Boltzmann machines[J]. Momentum, 2012, 9(1): 599-619. |
| [17] |
Kanda N, Takeda R, Obuchi Y. Elastic spectral distortion for low resource speech recognition with deep neural networks[C]//Automatic Speech Recognition and Understanding.[S.l.]: IEEE, 2013: 309-314. http://ieeexplore.ieee.org/document/6707748/
|
| [18] |
Kumar A, Florencio D. Speech enhancement in multiple-noise conditions using deep neural networks[C]//Proceedings of the Annual Conference of the International Speech Communication Association, INTERSPEECH.[S.l.]: [s.n.], 2016, 3738-3742. http://cn.arxiv.org/abs/1605.02427
|
 2018, Vol. 33
2018, Vol. 33

