空间Co-location模式(并置模式)挖掘是空间数据挖掘的重要分支,在地理科学、城市规划、公共交通和环境保护等领域有着广泛应用。Co-location模式是一组在空间中频繁关联的空间特征的子集,如学校附近往往有文具店;长苞冷衫树下往往会有松茸生长等。空间Co-location模式挖掘一般采用最小参与率(参与度)为度量标准的挖掘框架。将特征的参与率作为空间特征频繁性的度量指标,并使用参与度作为度量空间Co-location模式频繁性的指标,通过用户指定的参与度阈值对Co-location频繁模式进行挖掘。当参与度较高时,容易得到常识性结果。当参与度较低时,则会产生大量频繁但用户不感兴趣的模式,使得用户难以理解和识别有用的知识。
另外,虽然基于最小参与度的Co-location频繁模式挖掘体系能够较好地反映出空间特征并置的频繁程度,但由于计算模式特征参与率、参与度的过程中,没有考虑到空间实例之间的相互作用,如空间实例间的互相关性等,仅仅依靠参与率无法帮助用户挖掘到模式中特征之间的关系。例如:对于频繁模式{医院,药店,花店},特征“医院”、“药店”和“花店”的参与率分别是0.65,0.5和0.8。对模式频繁性贡献最高的是“花店”特征,事实上,“医院”是模式{医院,药店,花店}形成的关键因素。这说明仅仅依靠参与率无法判断医院对其他两个特征的影响。另外,按照基于最小参与率的类Apriori逐阶挖掘频繁模式的方法,子模式{药店,花店}必将作为一个频繁模式提供给用户,可能对用户造成误导。
基于以上思考,在挖掘到的大量频繁Co-location模式结果集中,进一步识别含有关键特征的模式,并摘取关键特征,将有效提高挖掘到的频繁模式的可用性,方便用户对挖掘结果的理解和使用。然而现有的参与率-参与度度量无法标识含有关键特征的频繁模式,也无法识别频繁模式中的关键特征。因此,本文提出空间Co-location模式的关键特征新概念;给出识别含有关键特征的频繁模式及摘取关键特征的方法。
识别空间Co-location模式的关键特征主要存在两方面的挑战。目前的方法主要关注于寻找模式中特征实例的频繁并置,忽略了不同特征对模式贡献的差异。因此,如何定义和度量含有关键特征的Co-location频繁模式及其关键特征是第一个挑战。面对挖掘到的大量Co-location模式,如何高效地挖掘含有关键特征的Co-location模式及关键特征集是第二个挑战。
1 相关工作空间Co-location模式挖掘最早由Huang[1]等提出,他们形式化定义了空间邻近关系、行实例、表实例、参与率以及参与度等概念,并提出了基于完全连接(Join-based)的空间Co-location模式挖掘算法。为解决Join-based算法中连接操作开销巨大的问题,基于部分连接(Partial-join)算法[2]和基于星型邻居扩展的无连接(Join-less)算法[3]被相继提出,这两种算法有效地减少了实例连接操作,算法效率在稠密数据集上均优于Join-based算法。研究人员对无连接Co-location挖掘方法进行进一步研究,提出了基于前缀树的挖掘算法:CPI-tree(Co-location pattern instances tree)算法[4]、ICPI-tree算法[5]和Order-Clique-Based算法[6]。其中,Order-Clique-Based算法在优化前缀树结构的基础上,通过生成候选极大Co-location模式和表实例,避免了存储所有侯选模式表实例产生的计算开销,从而显著地提高了挖掘效率。由于Co-location模式挖掘的广泛应用需求,研究人员提出了不同数据类型上的Co-location模式挖掘算法。针对不确定数据,Wang等[7]提出了不确定数据集上概率频繁的空间Co-location模式挖掘方法。针对模糊数据,欧阳志平等[8]提出了模糊参与率及模糊参与度概念来挖掘模糊数据的空间Co-location模式。针对变化的数据集,芦俊丽等[9]提出了空间Co-location模式增量挖掘并给出一系列挖掘算法。在针对特定目标的Co-location挖掘方面,Huang等[10]引入最大参与率概念解决带稀有特征的Co-location模式的挖掘问题;周剑云等[11]引入加权参与率(度)研究了基于加权欧氏距离的空间Co-location模式挖掘算法。为了有效地缩减频繁Co-location模式结果,去除冗余,闭Co-location模式挖掘算法[12],Co-location代表模式挖掘算法[13]等缩减模式结果的算法被提出。然而以上数据驱动的Co-location挖掘方法通常只依赖于数据和挖掘算法,忽略了数据特定的领域和用户的偏好,挖掘结果往往概括性差、无针对性,且包含大量用户不感兴趣的知识。为提高模式的可用性,研究人员在基于领域驱动的空间数据挖掘方面做出了大量的工作。杨世晟等[14]提出了高效用Co-location模式挖掘,芦俊丽等[15]则研究了高效用Co-location模式的增量挖掘。包旭光等提出了基于领域本体的Co-location规则挖掘方法[16],Fang等提出了组合Co-location模式挖掘方法[17],得到了更加精简有效的模式结果。
上述研究工作假设空间数据满足实例之间的独立性,然而在现实中,空间数据往往是高度相关的,例如时空轨迹数据挖掘[18]、基于社会媒体的旅游数据挖掘[19]等。本文工作考虑空间特征及实例之间的耦合关系[20-22],研究了含有关键特征的空间Co-location模式及其关键特征的挖掘和识别。
2 基本概念及相关定义 2.1 基本概念给定一个空间特征集合F={f1, f2,…, fn},一个与F对应的空间实例集合S={S1∪S2∪…∪Sn},一个空间邻近关系R,一个k阶空间Co-location模式c={f1, …, fk}(c∈F)及一组空间实例的子集l={i1, i2, …, ik}(l∈S)。若l包含c的所有特征且所有实例满足{R(ii, ij)|1≤i≤k, 1≤j≤k}并形成团,则l称为Co-location模式c中的一个行实例。Co-location模式c的所有行实例的集合L={l1, l2, …, lo}称为表实例,记为T(c),将每个特征看作一个一阶模式,特征的表实例表示该特征的所有实例的集合。为表示方便,本文中Iij代表特征fi的第j个实例。空间特征fi在k阶Co-location模式c={f1, …, fk}中的参与率是fi的实例在T(c)中不重复出现的个数与fi总实例个数的比率,即,
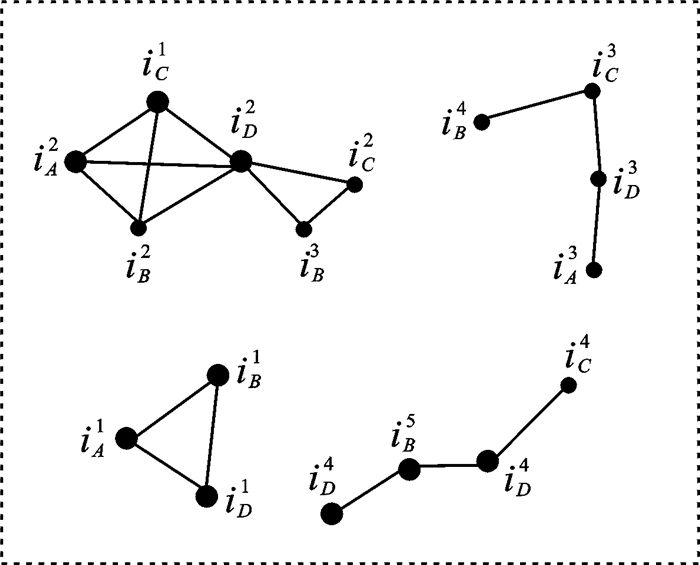
例1 如图 1所示,图中共有4个空间特征A, B, C和D,设其分别代表居民区、药店、花店及医院。空间特征A有4个实例iA1, iA2, iA3和iA4,空间特征B有5个实例iB1, iB2, iB3, iB4和iB5,空间特征C有4个实例iC1, iC2, iC3和iC4,空间特征D有4个实例iD1, iD2, iD3和iD4。设min_prev=0.4,Co-location模式{B, C, D}的参与度为: min(PR({B, C, D}, B), PR({B, C, D}, C), PR({B, C, D}, D))=min
|
图 1 1个空间实例集 Fig. 1 A data set |

|
图 2 一部分频繁模式表实例 Fig. 2 Table instances of prevalent Co-location patterns |
引理1[1]:(参与率与参与度的向下闭合性)参与率(PR)和参与度(PI)随着Co-location模式阶的增大单调递减。
传统Co-location挖掘没有考虑到特征之间、实例之间的耦合关系,本文通过分析频繁模式与其子模式间的关系、模式中特征内部实例间的关系和特征之间不同实例的关系,挖掘含有关键特征的模式,并识别关键特征。
2.2 相关定义传统Co-location挖掘算法采用参与率度量特征在模式中的作用。然而,这样的度量只考虑单个特征的实例参与到模式中的比例,没有考虑到特征和实例之间的相互作用。为了描述特征之间的相互作用,本文通过频繁模式与其所有直接子模式的参与率变化来分析新特征加入时,新特征对该模式中其他特征的影响。
定义1(参与损失率和参与损失度)
给定一个k(k>2)阶频繁Co-location模式c,设c′是c的一个k-1阶子模式,如果fi是c和c′的公共特征,fi关于c′和c的参与损失率(Participation_Loss_Ratio)定义为
| $ {\rm{PLR}}\left( {c,c',{f_i}} \right) = {\rm{PR}}\left( {c',{f_i}} \right) - {\rm{PR}}\left( {c,{f_i}} \right) $ | (1) |
引理1保证了0≤PLR(c, c′, fi)≤PR(c′, f)。
模式c对于模式c′的参与损失度(Participation_Loss_Index)PLI(c, c′)定义为两个模式中所有公共特征fi的PLR(c, c′, fi)值中的最小值:PLI(c, c′)=min{PLR(c, c′, fi)}
例2 Co-location模式{B, C, D}及其子模式{B, C}的表实例如图 2所示,则模式{B, C, D}对于模式{B, C}的参与损失度PLI({B, C, D}, {B, C})为
| $ \min \left\{ {{\rm{PLR}}\left( {\left\{ {B,C,D} \right\},\left\{ {B,C} \right\},B} \right),{\rm{PLR}}\left( {\left\{ {B,C,D} \right\},\left\{ {B,C} \right\},C} \right)} \right\} = \min \left\{ {0,0} \right\} = 0 $ | (2) |
模式参与损失率指的是特征fi从模式c′到模式c损失的参与率,损失率越小,说明c′参与到c中的行实例越多,其脱离fk的实例单独存在的行实例就越少,c′中的特征对特征fk的依赖越强。
Co-location模式的参与损失度通过分别计算特征参与在k阶Co-location模式c与其子模式c′的投影个数,得到c′模式随着新的特征fk加入形成模式c时其表实例的变化。其变化的程度体现fk对c′中特征的影响程度,即模式c中其他特征对fk的依赖程度。当模式中各特征对模式的贡献值有差异时,说明模式中特征地位不平等。容易观察到,对于含有关键特征的频繁Co-location模式,由于关键特征是使模式频繁的主要因素键特征对模式的贡献高于模式内其他特征。本文中,组成该模式的特征在模式中地位必然不平等,关提出模式显著性定量地度量含有关键特征的频繁Co-location模式。
定义2 (显著Co-location模式)
给定1个k(k≥2)阶频繁Co-location模式c={f1, f2,…, fk},其k个k-1阶子模式集记为Ck-1,设Pi(1≤i≤k,Pi∈Ck-1)为c的任一k-1阶子模式,则Co-location模式的显著性CDS(c)定义为
| $ {\rm{CDS}}\left( c \right) = \mathop {\max }\limits_{i = 1}^k \left( {{\rm{PLI}}\left( {c,{P_i}} \right)} \right) - \mathop {\min }\limits_{i = 1}^k \left( {{\rm{PLI}}\left( {c,{P_i}} \right)} \right) $ | (3) |
设min_cds(0≤min_cds≤1)是用户给定的最小显著性阈值,当CDS(c)≥min_cds时,称Co-location模式c是一个显著模式。
定义2合理性说明:PLI(c, c′)值越大,特征f∈c-c′的实例参与到模式c′的邻近关系中的比例越高,即f与c′中特征形成团的行实例比c′行实例中不与c′形成团的行实例越多,则f对模式c′中特征影响越大。反之,PLI(c, c″)值越小,说明特征f′∈c-c″的实例参与到模式c″中特征实例的邻近关系越少,即f′对模式c″中特征的影响越小。模式显著性越大,则模式c中至少有两个特征f与f′对模式的贡献度相差越大,即模式内特征地位对比越鲜明,越有可能含有关键特征。阈值的设定是为区分不同用户或不同应用对关键特征判定的差异。
例3 模式{B, C, D}及其子模式{B, C},{B, D},{C, D}的表实例如图 2,设min_cds=0.2,PLI({B, C, D}, {B, C})=0,PLI({B, C, D}, {B, D})=0.25, PLI({B, C, D}, {C, D})=0.2,模式{B, C, D}的模式显著性为:CDS({B, C, D})=0.25≥min_cds,则称模式{B, C, D}是一个显著的Co-location模式。
通过模式显著性阈值产生的显著Co-location模式筛选出了频繁Co-location模式中含有关键特征的Co-location模式,然而,模式中哪些特征为关键特征还需进一步分析。
空间特征之间和实例之间存在差异性是Co-location关键特征摘取的基础。下面通过同一特征的实例在表实例中出现的频率及不同特征间实例的相互影响对模式中特征的重要程度进行度量。
定义3 (特征重复率)
给定一个k阶频繁Co-location模式c={f1, f2, …, fk},该模式表实例为T(c),T(c)中行实例的集合为L={l1, l2, …, lt},特征fi∈c在T(c)中的重复率RR(Repeat_ratio)定义为
| $ RR\left( {c,{f_i}} \right) = 1 - \frac{{\left| {{\pi _{{f_i}}}\left( {T\left( c \right)} \right)} \right|}}{{\left| L \right|}} $ | (4) |
例4 如图 2 {B, C, D}的表实例中,特征D的实例在T({B, C, D})中的重复率为
| $ RR\left( {\left\{ {B,C,D} \right\},D} \right) = 1 - \frac{{\left| {{\pi _D}\left( {T\left( {\left\{ {B,C,D} \right\}} \right)} \right)} \right|}}{{\left| {{L_{\left\{ {B,C,D} \right\}}}} \right|}} = \frac{1}{3} $ | (5) |
式中:πfi(T(c))代表特征fi在T(c)中的投影,L代表行实例的全集,其比值表示fi在表实例中不重复出现的程度。特征的重复率刻划了该特征在模式中对其他特征的依赖程度,即特征重复率越高,该特征相同实例参与的行实例越多,对模式的贡献越大,且该特征在模式中受到其他特征的影响越小。换言之,特征模式度量了该特征在模式中受到的影响。
为进一步观察模式中特征之间的相互作用,通过统计各个特征对模式内其他特征的影响度分析特征对模式中其他特征造成的影响。
为方便表示一个Co-location表实例中各实例间的关系,首先提出一个特征间实例映射函数:
给定一个k阶频繁Co-location模式c={f1, …, fk},各特征在表实例T(c)中对应的实例集记为I={I1, I2, …, Ik},cl(jix)为ijx所在的行实例集合,特征间实例映射函数定义为
| $ {\pi _{j\xrightarrow{c}k}}\left( {i_j^x} \right) = \left\{ {i_j^x\left| {{\pi _{{f_k}}}\left( {cl\left( {i_j^x} \right)} \right) \subseteq {I_k}} \right.} \right\} $ | (6) |
式中:
例5 图 2中,对于模式
定义4 (特征影响度)
给定一个k阶频繁Co-location模式c ={f1, f2 …, fk},该模式表实例为T(c),T(c)中各个特征实例的集合为I={I1, I2, …, Ik},则特征fi对整个模式c的影响度(Co-location effect index, CEI)定义为
| $ {\text{CEI}}\left( {c,{f_i}} \right) = \frac{1}{{\left| {k - 1} \right|}}\sum\limits_{1 \leqslant j \leqslant k,j \ne i} {\left( {\frac{1}{{{I_i}}}\sum\limits_{i_i^x \in {I_i}} {\left( {{\pi _{j\xrightarrow{c}k}}\left( {i_j^x} \right)} \right)} } \right)} $ | (7) |
例6 如图 2中,特征D对模式{B, C, D}的影响度CEI({B, C, D}, D)为
| $ \begin{array}{l} \frac{1}{2} \times \left( {\frac{1}{3} \times \left( {\left| {{\pi _{D \to B}}\left( {i_D^1} \right)} \right| + \left| {{\pi _{D \to B}}\left( {i_D^2} \right)} \right| + \left| {{\pi _{D \to B}}\left( {i_D^3} \right)} \right|} \right) + \frac{1}{3} \times \left( {\left| {{\pi _{D \to C}}\left( {i_D^1} \right)} \right| + } \right.} \right.\\ \;\;\;\;\left. {\left. {\left| {{\pi _{D \to C}}\left( {i_D^2} \right)} \right| + \left| {{\pi _{D \to C}}\left( {i_D^3} \right)} \right|} \right)} \right) = \frac{4}{3} \end{array} $ | (8) |
定义5 (特征关键度和模式关键度)
给定一个候选k阶Co-location频繁模式c ={f1, f2,…, fk},特征fi在c中的关键度定义为
| $ KR\left( {c,{f_i}} \right) = {\rm{CEI}}\left( {c,{f_i}} \right) \times \left( {RR\left( {c,{f_i}} \right) + 1} \right) $ | (9) |
其中RR(c, fi)+1保证了KR值的非负性。模式关键度(Key_Index)定义为该模式中所有特征关键度的最大值:
考虑到实际应用中用户需求的差异,设置一个最小关键度阈值min_key(0≤min_key≤1)。由于KR(c, fi)是一个大于1的值,为方便关键度阈值的设定,将c中特征的关键度归一化为
由于模式关键度KI(c)定义为该模式中所有特征关键度的最大值,而最小关键度阈值是介于0到1之间的值,模式c有且至少有1个关键特征fi,其特征关键度大于所有模式c中其他特征,即
本文提出了一个Co-location关键特征挖掘框架,通过模式与模式之间、空间特征之间和实例之间的相互影响,对含有关键特征的Co-location模式及其关键特征集进行挖掘。为了减少计算表实例的巨大开销,对于一个Co-location频繁模式集中的任意一个Co-location模式,首先分析其直接子模式集与该模式的关系,基于频繁模式进行显著性分析,得到显著Co-location模式集合;然后,对显著Co-location模式集中的任意一个Co-location模式,分析特征内部实例间的相关性及不同特征的实例之间的相关性;在给出一系列度量对模式及其关键特征进行评价,最后得到含有关键特征的Co-location模式及其关键特征集。
3.1 显著Co-location模式挖掘根据用户给定的最小显著性阈值min_cds,从所有频繁Co-location模式中挖掘出显著Co-location模式。最直接的方法是在挖掘到的频繁Co-location模式集上进行2次挖掘。然而,由于计算一个Co-location模式的显著性需要用到该模式和其直接子模式的表实例,当数据量较大时,表实例的存储耗费了大量存储空间,为了提高计算效率,将显著性计算融入到频繁Co-location模式的挖掘过程中,以避免存储及输出所有频繁模式表实例带来的巨大内存耗费和I/O开销。具体见类似Join-less的算法1。
算法1 SK算法
输入:空间数据集S,空间特征集F,空间实例集I,距离阈值d,最小参与度阈值min_prev,显著性阈值min_cds
输出:显著Co-location频繁模式集SCP
变量:k :Co-location模式的阶, Ck :k阶Co-location候选频繁模式集, Pk : k阶Co-location频繁模式集, PR_c: k阶Co-location频繁模式c的参与率集
步骤:
1. SN=gen_star_neighborhoods(F, S, d); //生成星型邻居集
2. P1 =F, k=2, SCP=∅
3. WHILE(Pk-1≠∅)DO
4. Ck = gen_candidate_colocation(k, Pk-1)//生成k阶候选
5. FOR EACH c∈Ck DO
6. IF calculate PI(c) ≥min_prev DO//计算模式参与度
7. FOR EACH p∈Pk-1(c) DO
8. calculate PLI(c, p); //计算模式损失度
9. END DO
10. IF calculate CDS (c) ≥min_cds DO//计算显著性
11. keyset(c)←sel _key_f(c, Table_ins (c), min_key); //摘取关键特征
12. SCP←{c, keyset(c)};
13. END DO
14. END DO
15. END DO
16. k= k+1;
17. END DO
行1根据距离阈值生成星型实例集;行2—4生成k阶Co-location候选模式集;行5—15描述含有关键特征的频繁模式识别及关键特征摘取过程:行5—6计算参与度;行7—9对于满足参与度阈值的模式,与该模式的直接子模式集合计算模式损失度;行10中,若得到的模式显著性大于给定的显著性阈值min_cds,那么行11计算其关键特征集;行12将含有关键特征的频繁模式及其关键特征进行存储;随着Co-location模式阶数的增长,行3—16被反复执行,最后得到了显著Co-location模式集合及其关键特征集。
3.2 Co-location关键特征摘取该算法是算法1中关键特征摘取的子过程,通过分析显著Co-location模式表实例中特征内部实例之间的关系及不同特征的实例之间的影响,对模式的关键特征进行摘取。根据这一思想,提出关键特征摘取算法。
算法2 sel _key_f算法
输入:显著Co-location频繁模式scp,Table_scp显著Co-location频繁模式的表实例,关键程度阈值min_key
输出:显著Co-location频繁模式的关键特征集KeySet
变量:min_key:最小关键度阈值,Candidate_KeyF:关键特征候选集
步骤:
1. KeySet=∅;
2. FOR EACH feature∈scp DO
3. calculate (RR(Table_scp, feature)); //计算实例重复率
4. calculate (CEI(Table_scp,feature)); //计算特征影响度
5. calculate (KR(Table_scp,feature)); //计算模式关键率
6. END DO
7. calculate(KI(scp))); 计算模式关键度
8. FOR EACH feature∈scp DO
9. IF(KR(Table_scp,feature)/ KI(scp)≥min_key)DO
10. KeySet (scp)←feature; //摘取关键特征
11. END DO
12. END DO
行1初始关键特征集合;行2—6描述了计算显著Co-location模式scp中所有特征的关键度的过程:行3计算scp中特征内部实例重复率;行4计算scp中特征对模式的关键度;行5计算所有特征的关键率;循环执行2—6行直至计算完所有特征的关键率;行7根据所有特征的关键率得到模式关键度;行8—9测试关键特征;行10将关键率大于最小关键度阈值的特征加入关键特征集合中;循环行8—12得到所有关键度超过最小关键阈值的特征。
4 实验与分析本节将在合成数据和真实数据上详细地验证算法的效率和效果。实验评估主要从以下几方面进行:SK算法在不同数据集上的性能分析;SK算法与经典的Join_less频繁模式挖掘算法[3]的实验效果比较;空间关键特征挖掘算法在真实数据上的应用。所有算法均在core i3, 2.4 GHz CPU和8GB内存的PC机上用C#语言实现。
本文一共选取了4个不同规模的合成数据集和2个真实数据集验证算法的性能及挖掘效果。真实数据集分别来自北京市部分地区的POI数据和“三江并流区域”植被数据。北京市POI数据含有26 546个空间实例及16个空间特征,“三江并流区域”植被数据含有335个空间实例及32个空间特征。表 1显示了各数据集的大小、特征个数以及数据集的来源。实验所采用的合成数据均是根据泊松分布随机产生,并均匀分布在1 000 ×1 000空间里。
| 表 1 数据集 Tab. 1 Experimental data sets |
本文将传统Co-location频繁模式的挖掘结果与本文提出的SK算法进行比较,验证挖掘的效果。
4.1 合成数据集上的SK算法性能分析本文在多个合成数据集上用空间Co-location关键特征挖掘算法(SK算法),与传统挖掘算法的挖掘结果进行实验比较。传统算法采用了经典的Join_less算法。考虑实例个数、参与度阈值、距离阈值以及显著性阈值对两种算法的影响。表 2显示了合成数据实验中的默认参数。
| 表 2 实验数据的参数说明 Tab. 2 Default parameter description |
4.1.1 参与度阈值对SK算法的影响
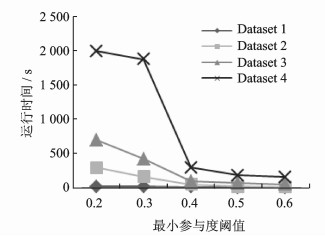
本节考虑变化的最小参与度阈值对SK算法性能的影响。图 3显示在0.2, 0.3, 0.4, 0.5和0.6五个不同的距离阈值上运行SK算法的性能。对于每个数据集,当最小参与度阈值增大时,运行时间逐渐减少。对于所有数据集,随着数据规模的增加和最小参与度阈值的减少,其运行时间逐渐增加。对于数据集dataset4,最小参与度阈值对算法性能的影响尤其明显,这是因为在阈值较低且数据较为稠密的情况下,模式的表实例较大,对表实例的运算的耗费影响了算法性能。
|
图 3 参与度阈值在不同数据集上的性能比较 Fig. 3 Comparison of running time with different min_prev on synthesized data sets distance thresholds on synthesized data sets |
4.1.2 距离阈值对SK算法的影响
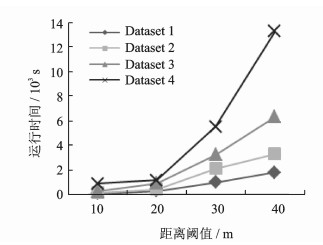
本节考虑变化的距离阈值对SK算法性能的影响。图 4显示在10, 20, 30和40四个距离阈值上运行SK算法的性能。对于每个数据集,当距离阈值增大时,运行时间逐渐减少。对于所有数据集,随着数据规模和距离阈值的增加,其运行时间逐渐增加。距离阈值较大时,算法性能的影响尤其明显,这说明算法性能主要受到数据稠密性的影响。
|
图 4 距离阈值在不同合成数据集上的性能比较 Fig. 4 Comparison of running time with different |
4.1.3 显著性阈值对SK算法的影响
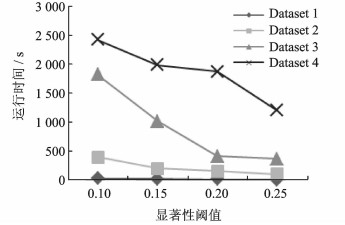
本节考虑变化的显著性阈值对SK算法性能的影响。图 5显示在0.1, 0.15, 0.2和0.25四个显著阈值上运行SK算法的性能。对于每个数据集,当显著性阈值增大时,运行时间减少较快。因为随着显著性阈值的升高,需要计算的频繁模式表实例减少,显著性阈值的变化对稠密数据集上算法性能的影响更加明显。
|
图 5 显著性阈值在不同数据集上的性能比较 Fig. 5 Comparison of running time with different min_cds on synthesized data |
4.2 真实数据集上的SK算法与Join_less算法比较
在本节,本文将空间Co-location关键特征挖掘算法与传统挖掘算法的挖掘结果在真实数据上进行实验比较。由于SK算法针对挖掘含有关键特征的模式,并非进行低损失率的模式压缩,相较于模拟数据,真实数据的挖掘结果更有实际意义。
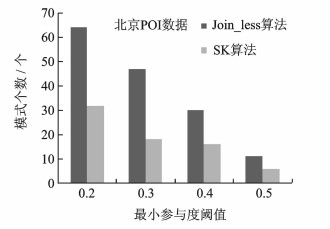
4.2.1 SK算法在北京POI数据集上的结果比较图 6显示POI数据在距离阈值为50,显著性阈值为0.2,特征关键度为0.3的条件下通过变化的最小参与度阈值观察SK算法产生含有关键特征的频繁模式的结果。
|
图 6 不同参与度阈值在POI数据集上的挖掘效果比较 Fig. 6 Comparison of mining results with different setsmin_prev on POI data set |
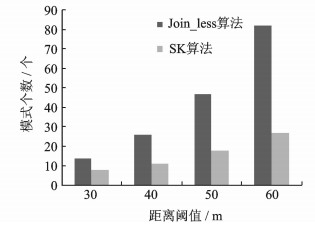
图 7显示POI数据参与度阈值为0.3,显著性阈值为0.2,特征关键度为0.3的条件下通过距离阈值的变化观察SK算法产生含有关键特征的频繁模式的结果。
|
图 7 不同距离阈值在POI数据集上的挖掘效果比较 Fig. 7 Comparison of mining results with different distance thresholds on Beijing POI data set |
4.2.2 SK算法在植被数据集上的结果比较
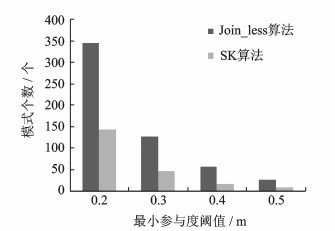
图 8显示植被数据在距离阈值为6 000,显著性阈值为0.2,特征关键度为0.3的条件下通过最小参与度阈值的变化观察SK算法产生含有关键特征的频繁模式的结果。
|
图 8 不同参与度阈值在植被数据集上的挖掘效果比较 Fig. 8 Comparison of mining results with different min_prev on vegetation data set |
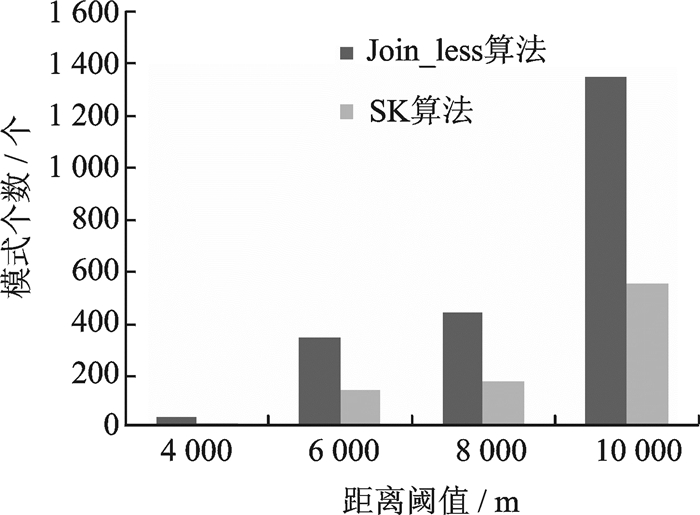
图 9显示植被数据在最小参与度阈值为0.3,显著性阈值为0.2,特征关键度为0.3的条件下通过距离阈值的变化观察SK算法产生含有关键特征的频繁模式结果。
|
图 9 不同距离阈值在植被数据集上的挖掘效果比较 Fig. 9 Comparison of mining results with different distance thresholds on vegetation data set |
4.3 实例分析
含有关键特征的Co-location模式挖掘目的是识别显著性模式及其关键特征、缩减模式结果并提高模式的可用性。上述在模拟数据集和真实数据集上的实验已经证明SK算法能够有效地减少模式结果,使挖掘结果只留下含有关键特征的频繁模式及其关键特征,因此,该方法更具有针对性和用户实用性。
4.3.1 模式挖掘结果实例分析本节在北京POI数据集上将频繁模式挖掘结果与含有关键特征的模式挖掘结果进行对比。通过实验结果可看出SK算法能够有效地识别频繁模式中含有关键特征的模式并摘取关键特征,过滤由于频繁模式向下闭合性产生的可能给用户带来误导的子模式,达到了较好的应用效果。
本节仅以三阶频繁模式及含有关键特征的模式为例,北京POI数据集在21个三阶模式中识别出5个含有关键特征的模式及其关键特征。表 3列出了含有关键特征的频繁模式,给出了每个模式的参与度、模式显著性和模式关键度,将模式通过关键度排序。其中,模式的关键特征用粗体标识。
| 表 3 真实数据集关键特征挖掘结果 Tab. 3 Mining results of key features on real data set |
从表 3中可以看出,含有关键特征的模式在保持模式频繁的基础上对模式进一步分析后,得到的模式及其关键特征更好地对模式进行了解释,使得用户面对更加精简的模式结果时更易理解和使用。
4.3.2 关键特征摘取实例分析本节以含有关键特征的{酒店, 公园, 停车场}的Co-location频繁模式为例,观察参与率与关键度两种模式特征度量方法的区别。从表 4中可以看出,当设关键度阈值min_key=0.2时,酒店和公园是模式{酒店, 公园, 停车场}模式的关键特征,且其关键度度量通过对模式中特征实例的相关性分析,得出更有针对性、更有指导性的结果。
| 表 4 真实数据集关键特征度量值 Tab. 4 Metrics of key features on real data set |
5 结束语
本文根据Co-location频繁模式挖掘结果数量大、针对性不足的问题,为让用户更好地理解和使用挖掘结果,提出了含有关键特征的频繁Co-location模式及其挖掘算法。本文针对含有关键特征的空间Co-location模式挖掘问题, 给出了一系列相关定义、度量标准和挖掘算法。通过大量的实验表明,本文提出的算法能够有效地缩减模式结果,为用户提供含有关键特征的Co-location模式和相应的关键特征,为特定应用提供有效的支持。下一步的工作将在此基础上,通过特征提取和数据压缩等方法减少挖掘过程中产生的Co-location表实例的存储和计算开销,进一步提高该算法的效率。
| [1] |
Huang Y, Shekhar S, Xiong H. Discovering colocation patterns from spatial data sets:A general approach[J]. IEEE Transactions on Knowledge and Data Engineering (TKDE), 2004, 16(12): 1472-1485. DOI:10.1109/TKDE.2004.90 |
| [2] |
Yoo J S, Shekhar S. A partial join approach for mining colocation patterns[C]//The ACM International Symposium on Advances in Geographic Information System (ACM GIS). Washington USA: ACM, 2004: 241-249.
|
| [3] |
Yoo J S, Shekhar S, Celik M. A join-less approach for colocation pattern mining: A summary of results[C]//The IEEE International Conference on Data Mining (ICDM). Houston, USA: IEEE, 2005: 813-816.
|
| [4] |
Wang L Z, Bao Y Z, Lu J, et al. A new Join-less approach for co-location pattern mining[C]//Proceedings of the IEEE 8th International Conference on Computer and Information Technology (CIT 2008). Sydney, Australia: IEEE, 2008: 197-202.
|
| [5] |
Wang L Z, Bao Y Z, Lu Z. Efficient discovery of spatial co-location patterns using the iCPI-tree[J]. The Open Information Systems Journal, 2009, 3(1): 69-80. |
| [6] |
Wang L Z, Zhou L H, Lu J, et al. An order-clique based approach for mining maximal colocations[J]. Information Sciences, 2009, 179(19): 3370-3382. DOI:10.1016/j.ins.2009.05.023 |
| [7] |
Wang L Z, Wu P P, Chen H M. Finding probabilistic prevalent co-locations in spatially uncertain data sets[J]. IEEE Transactions on Knowledge and Data Engineering (TKDE), 2013, 25(4): 790-804. DOI:10.1109/TKDE.2011.256 |
| [8] |
欧阳志平, 王丽珍, 陈红梅. 模糊对象的空间Co-location模式挖掘研究[J]. 计算机学报, 2011, 34(10): 1947-1955. Ouyang Zhiping, Wang Lizhen, Chen Hongmei. Mining spatial Co-location patterns for fuzzy objects[J]. Chinese Journal of Computers, 2011, 34(10): 1947-1955. |
| [9] |
芦俊丽, 王丽珍, 肖清, 等. 空间Co-location模式增量挖掘及演化分析[J]. 软件学报, 2014, 25(S(2)): 189-200. Lu Junli, Wang Lizhen, Xiao Qing, et al. Incremental mining and evolutional analysis of Co-locations[J]. Journal of Software, 2014, 25(S(2)): 189-200. |
| [10] |
Huang Y, Pei J, Xiong H. Mining co-location patterns with rare events from spatial data sets[J]. GeoInformatica, 2006, 10(3): 239-260. DOI:10.1007/s10707-006-9827-8 |
| [11] |
周剑云, 王丽珍, 杨增芳. 基于加权欧氏距离的空间Co-location模式挖掘算法研究[J]. 计算机科学, 2014, 41(S1): 425-428. Zhou Jianyun, Wang Lizhen, Yang Zengfang. Algorithm of mining spatial Co-location patterns based on weighted euclidean distance[J]. Computer Science, 2014, 41(S1): 425-428. |
| [12] |
Yoo J S, Bow M. Mining top-k closed co-location patterns[C]//The IEEE International Conference on Spatial Data Mining and Geographical Knowledge Services (ICSDM 2011). Fuzhou, China: IEEE, 2011: 100-105.
|
| [13] |
Liu B, Chen L, Liu C, et al. RCP mining:Towards the summarization of spatial co-location patterns[M]. Springer International Publishing, 2015: 451-469.
|
| [14] |
杨世晟, 王丽珍, 芦俊丽, 等. 空间高效用Co-location模式挖掘技术初探[J]. 小型微型计算机系统, 2014(10): 2302-2307. Yang Shisheng, Wang Lizhen, Lu Junli, et al. Primary exploration for mining spatial high utility Co-location patterns[J]. Journal of Chinese Computer Systems, 2014(10): 2302-2307. DOI:10.3969/j.issn.1000-1220.2014.10.020 |
| [15] |
Wang X X, Wang L Z, Lu J L, et al. Effectively updating high utility co-location patterns in evolving spatial databases[C]//17th Web-Age Information Management. Nanchang, China: Springer-Verlag, 2016: 67-79.
|
| [16] |
包旭光, 王丽珍, 方圆. OSCRM:一个基于本体的空间Co-location规则挖掘框架[J]. 计算机研究与发展, 2015, 52. Bao Xuguang, Wang Lizhen, Fang Yuan. OSCRM:A framework of ontology-based spatial Co-location rule mining[J]. Journal of Computer Research and Development, 2015, 52(S): 74-80. |
| [17] |
Fang Y, Wang L Z, Lu J L, et al. A combined co-location pattern mining approach for post-analyzing co-location patterns[C]//International Conference on Artificial Intelligence: Technologies and Applications. Bangkok, Thailand: Atlantis Press, 2016: 38-43.
|
| [18] |
吉根林, 赵斌. 时空轨迹大数据模式挖掘研究进展[J]. 数据采集与处理, 2015, 30(1): 47-58. Ji Genlin, Zhao Bin. Research progress in pattern mining for big spatio-temporal trajectories[J]. Journal of Data Acquisition and Processing, 2015, 30(1): 47-58. |
| [19] |
高新波, 沈钧戈. 基于社会媒体的旅游数据挖掘与分析[J]. 数据采集与处理, 2016, 31(1): 18-27. Gao Xinbo, Shen Junge. Social media based travel data mining and analysis[J]. Journal of Data Acquisition and Processing, 2016, 31(1): 18-27. |
| [20] |
Wang C, Cao L, Wang M, et al. Coupled nominal similarity in unsupervised learning[C]//ACM Conference on Information and Knowledge Management(CIKM 2011). Glasgow, United Kingdom: ACM, 2011: 973-978.
|
| [21] |
Wang C, She Z, Cao L. Coupled clustering ensemble: Incorporating coupling relationships both between base clusterings and objects[C]//29th IEEE International Conference on Data Engineering(ICDE 2013). Brisbane, Australia: IEEE, 2013: 374-385.
|
| [22] |
Wang C, She Z, Cao L. Coupled attribute analysis on numerical data[C]//23th International Joint Conference on Artificial Intelligence (IJCAI 2013). Beijing, China: AAAI Press, 2013: 1736-1744.
|
 2018, Vol. 33
2018, Vol. 33

