人体重心是反映人体形态结构和质量分布特征的基本参数,在体育运动和医疗康复等领域有着重要的作用,因此人体重心的测量具有重要的学术和应用价值[1]。人体重心的测量方法主要有测力板法、穿戴设备和影像解析法[2]。测力板法是利用力传感器计算出人站在测力台上的压力中心[3],它可以提供较精确的重心位置测量,如文献[3]中为提高灵敏度设计了一种用于人体静态平衡研究的多维力传感器的测力台, 并对Footscan压力平板测试系统的重复性和可靠性进行了研究。但测力板设备体积较大不便携带,测量范围受到测力板面积的局限。穿戴设备法主要依据足底的重力传感器,根据静力学中的力矩平衡方程式进行重心位置的二维坐标测量,可提供灵活的运动测量范围[4]。如文献[5]提出了一种基于应变式压力传感器的可穿戴设备的重心计算方法,能由穿戴者的足底力准确地测量计算出相应的实时重心位置, 但是穿戴设备设备较为昂贵,重心测量的精度也有待改善,难以获取人体竖直方向的重心位置,影响了其推广。
随着影像测量在体育科学研究中的广泛应用,影像解析法逐渐被重视。影像解析法即从运动技术的相片或录像中获取人体环节重心或关节点坐标位置,依据人体通用模型测定人体重心,可大致分为分析法(又称力矩合成法)[6]和合成法,其中应用较广泛的是分析法,通常对录像解析法不作区分时指的就是该方法。分析法依据重心坐标公式,通过身体各环节相对重量和各环节重心位置计算获得人体重心位置[7]。若向计算机输入的是人体各环节中心点的坐标,该方法需要通过各环节中心坐标计算出环节重心坐标,显然增加了不必要的计算,于是文献[8]中介绍了乘系数法,该方法的计算过程更加简便迅速,在下文中将给出详细介绍。录像解析法过度依赖于人体通用模型,采用不同的人体通用模型往往得出不同的重心位置,且相对于测力台法和重心板法的误差较大,但却可以通过计算估计人体三维重心坐标。此外,随着技术的发展,还出现了使用运动捕捉[9]设备获得人体运动生物力学数据并以此得到重心的方法。例如:文献[10]通过获取的人体环节重心结合力矩合成法获得重心的坐标位置;文献[11]认为人体的密度是均匀的,并认为身体的体积中心就是人体的重心。但这些方法通常依赖于精密而昂贵的设备,实施起来比较复杂,如Optotrak Certus和Vicon的光学动作捕捉系统(8 Vicon MXF40 cameras)等。Kinect体感交互设备是微软发布的一种典型的红绿蓝(Red green blue, RGB)带深度测度的光学传感器[12-13],现已被应用于医疗康复和运动训练等领域,使用Kinect提供的人体关节点坐标位置可以获取人体重心,如文献[14]使用Kinect设备提供的20个关节点坐标通过力矩合成法获取人体三维重心坐标;文献[15]结合Optotrak Certus设备对Kinect获取的重心进行验证,其中计算重心的方法为力矩合成法;文献[16]利用单台Kinect对人体进行高精度、个性化建模。但Kinect提供的数据为关节点中心坐标而非环节重心坐标,研究问题需要解决实时捕捉人体的重要关节点,并将关节点计算环节重心坐标,进一步利用环节重心计算人体重心。
本研究的目的是针对以上重心测量方法,寻找一种利用Kinect提供的关节点坐标位置,快速、动态地获得人体重心三维坐标位置,并且计算方便快捷、具有扩展性的重心计算方法。本文利用FootScan获取到的压力重心数据对其可用性和准确性进行验证。
1 人体重心计算方法 1.1 力矩合成法人体重心计算力矩合成法是在获得身体各关节中心坐标值的基础上,将其乘上相应的系数,其乘积总和即为人体总重心的坐标值[8]。依据4种有关人体重心的资料得出每种资料下的乘系数法人体重心计算公式的系数。该系数是二维空间坐标系下的系数,人体重心坐标为
| $ {X_{\rm{c}}} = \frac{{\sum {x_i}*{P_i}}}{P} $ | (1) |
| $ {Y_{\rm{c}}} = \frac{{\sum {y_i}*{P_i}}}{P} $ | (2) |
式中:xi,yi为环节重心坐标;Pi为环节重量;P为人体重量。
根据人体环节惯性参数应用时的一般原则,忽略统计模型、性别和民族的差异,并且目前人体运动环节惯性参数的测量应用中还忽视了人体左右侧发展的不平衡,这为笔者提供了继续深入研究的可能性。结合Kinect设备和具体实验环境,选择目前使用较普遍的由德国资料得出的系数作为本研究中乘系数法的系数。计算人体重心位置的公式为
| $ {G_{{\rm{pos}}}} = \sum {k_i}*{J_i} $ | (3) |
式中:Gpos表示重心位置;Ji表示人体某环节的位置;ki表示该环节对应的系数。
1.2 体感交互设备Kinect的重心计算法由于利用体感交互设备Kinect可以直接获取人体25个关节点的坐标信息,所以使用力矩合成法的改进方法“乘系数法”进行线性累和的方法计算重心,相较于力矩合成法省去了通过关节点坐标计算环节重心坐标的计算过程,减少了重心计算步骤,节约了计算时间,更有利于实时获取重心的目标。本研究选择目前使用较普遍的由德国人体重心资料提供的关节系数构建人体重心计算模型,该模型共包含19个人体关节点。然而,利用Kinect获取的人体25个关节点并不能与系数合成法中的关节点一一对应,具体表现在:
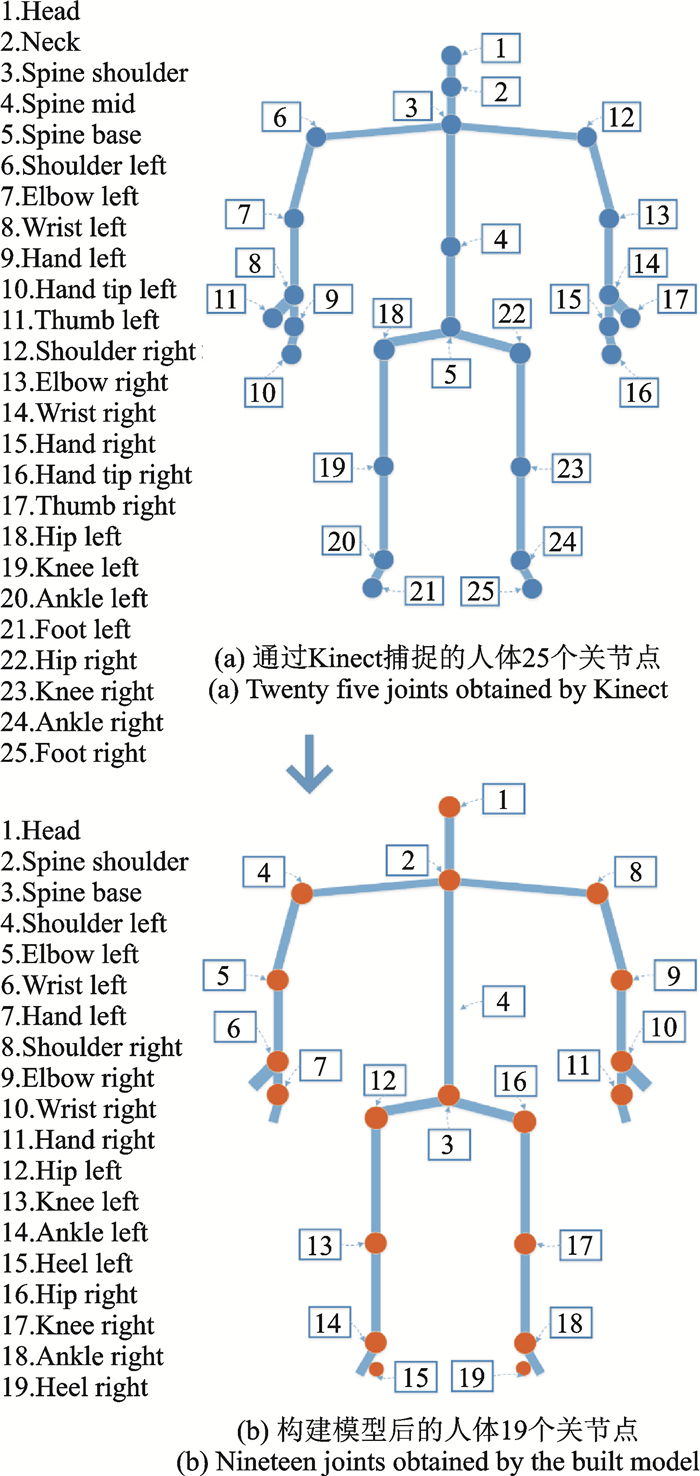
(1) 通过Kinect无法获取脚跟的坐标,但是其提供了脚掌(Foot left,Foot right)和脚踝(Ankle left,Ankle right)的坐标。在Kinect的3D坐标系中,脚跟的水平方向(X和Y方向)的坐标与脚踝相同,竖直方向(Z方向)的坐标与脚掌相同,那么脚跟的坐标就可以由脚掌和脚踝的坐标获得。
(2) 通过Kinect可以获得手掌、手指和大拇指的坐标,但只需要手的重心坐标,所以要求被试者握拳使3个关节点尽可能相近,这样得到的手(Hand left,Hand right)的坐标作为手重心的坐标。另外,如脖子(Neck)、脊柱中点(Spine mid)等关节点均未使用。
利用Kinect获取的人体关节点和构建力矩合成法模型后的人体各模块点的中心点如图 1所示,该模型中的人体各模块点及其对应系数见表 1。根据Kinect的采集数据计算得到的人体重心的X和Y方向值分别为
| $ {X_{\rm{c}}}\left( t \right) = \sum\limits_{i = 1}^{19} {{k_i}*{X_i}\left( t \right)} $ | (4) |
| $ {Y_{\rm{c}}}\left( t \right) = \sum\limits_{i = 1}^{19} {{k_i}*{Y_i}\left( t \right)} $ | (5) |
|
图 1 人体关节点 Fig. 1 Human body joints |
| 表 1 人体环节及其系数 Tab. 1 Human joints and their coefficients |
式中:ki为表 1中的对应系数;Xi(t)和Yi(t)分别为人体构建模型后各模块中心位置的X和Y坐标分量;Xc和Yc为由Kinect数据计算出的人体重心的X和Y坐标位置分量。
2 数据采集与处理 2.1 实验对象受试对象为3名课题小组成员1男2女,年龄25,26岁,无明显平衡及相关的肌肉神经疾病,健康状况良好。
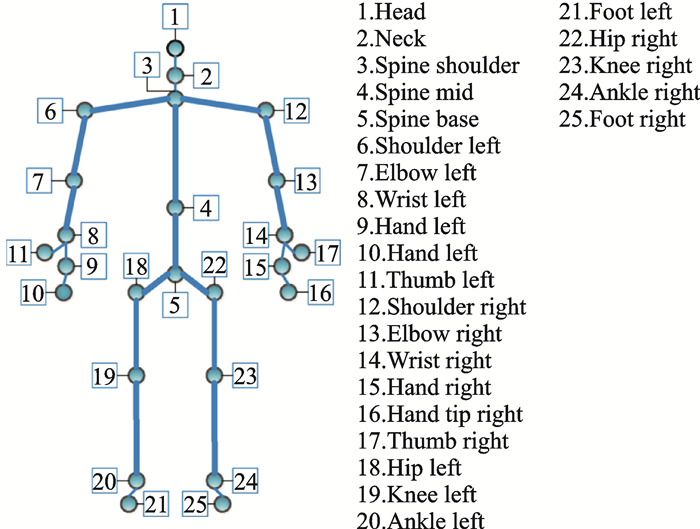
2.2 数据采集 2.2.1 Kinect所采用的第二代Kinect体感交互设备(Kinect for Windows v2 sensor)是一台集成RGB摄像头和红外摄像头的光学传感器[15],能够为本研究提供人体关节点的三维坐标信息。各关节点在人体中的位置如图 2所示。采样频率为30 Hz,但实际应用中的采样频率并不十分精确,通常在30 Hz左右。
|
图 2 Kinect追踪的三维关节点 Fig. 2 3D skeleton joints tracked by Kinect |
2.2.2 Footscan平板压力测试系统
采用Footscan(一米板)平板压力测试系统所提供的压力中心(Center of force,COF)数据作为本研究的标准数据,对Kinect下利用乘系数法得到的重心数据进行验证。Footscan平板压力测试系统的特点是具有较高的采样频率(最高达500 Hz,本实验采样频率为30 Hz)和较大的作用面积(1 m板和2 m板),现已被广泛的用于生物力学测试。
2.3 实验过程被试者裸足站在Footscan平板上,并将Kinect正对被试者放置于高度为25 inch(约63.5 cm)的Kinect 2.0三角支架上,使被试始终在视野范围内。实验开始时,两台仪器同时记录采集到的数据,并保存到计算机中。为了比较Kinect在不同幅度动作下测量重心的准确性,设立大幅动作、小幅动作和静止站立动作实验。在实验中被试者在保持站立的姿势下,最大幅度向四周作自由运动,要求保持全身挺直且双脚不能挪动。
本实验只考虑了与身体平行的左右方向(X方向)和与身体垂直的前后方向(Y方向)的坐标位置。由于Footscan只能提供X,Y两个方向的坐标数据,所以无法对人体高度的竖直方向上进行讨论。
2.4 数据处理 2.4.1 基于Kinect的关节数据处理和重心计算在Kinect的25个关节点中,并没有提供脚跟的坐标位置,所以并不是所有的关节都能与乘系数法中的关节作到一一对应,但是其提供了脚掌(Foot left,Foot right)和脚踝(Ankle left,Ankle right)的坐标位置。在实验中人体直立、运动不剧烈的情况下,脚踝的弯曲程度较小,可以认为在Kinect的3D坐标系中,脚跟的X和Y方向的坐标与脚踝相同,竖直方向的坐标与脚掌相同,即脚跟的坐标可由脚掌和脚踝的坐标获得。由式(3)根据Kinect获得的关节位置计算出重心位置。
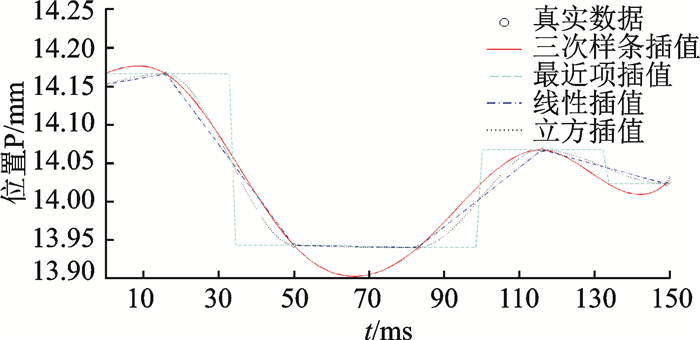
2.4.2 插值法选取由于两设备采样频率不同,计算时Kinect采集到的重心数据时间序列Kt不一定与Footscan采集到的重心数据时间序列Ft的采样值全部对应,因此需要利用插值法估算Kt在对应时刻的取值。利用Matlab插值工具箱中的一维插值函数,该函数包含4种基本的插值方法:三次样条插值、最近项插值、线性插值和立方差值。不同插值法比较如图 3所示,图中最近项插值和线性插值的光滑性较差,而立方插值在部分区域插值后的拟合效果较差(特别是在t∈[50, 80]处),所以选用三次样条插值法[21]进行计算。
|
图 3 不同插值法比较 Fig. 3 Comparison of different interpolation methods |
2.4.3 时序数据曲线
Footscan的压力测试系统由RSscan公司官方的数据采集软件提供,而Kinect的数据采集程序由笔者开发。由于两者分立于两个系统,所以需要额外的人工操作,在数据采集过程中无法做到绝对同步,两者数据采集时刻存在一定的先后差异,约0~3 s。
基本思路:设置采集时刻差异下限tmin和上限tmax,即两设备开始采集的时刻差Δt,满足:tmin≤Δt≤tmax,然后固定Ft,移动Kt,每次移动步长为1 ms,移动距离i(i∈[tmin, tmax]),利用三次样条插值法获得Kt对应Ft时刻的坐标位置估值,然后求Ft和Kt在对应时刻的距离并累加,得到对应时刻的距离之和Di,最后对所有的Di排序,最小值所对应i即时差Δt的取值,可表示为
| $ {D_i} = \sum\limits_{i = 2}^n {\left| {{F_{it}} - {K_{it}}} \right|} $ | (6) |
| $ \Delta t = {\rm{min}}({D_i}) \to i $ | (7) |
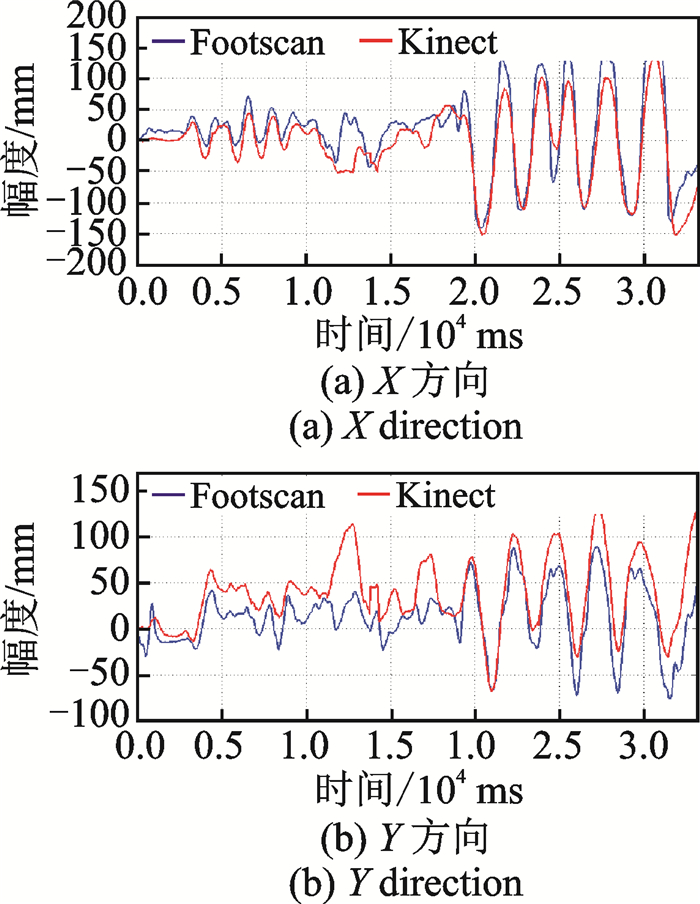
图 4—6为在3组动作下分别测得的两设备的重心轨迹示例,其中动作1为头、肩及躯干部位各向幅度较大的动作,动作2为身体前倾的动作,动作3为裸足静止站立时的动作。
|
图 4 动作1重心变化曲线 Fig. 4 Center of gravity change curve of action 1 |

|
图 5 动作2的重心变化曲线 Fig. 5 Center of gravity change curve of action 2 |
|
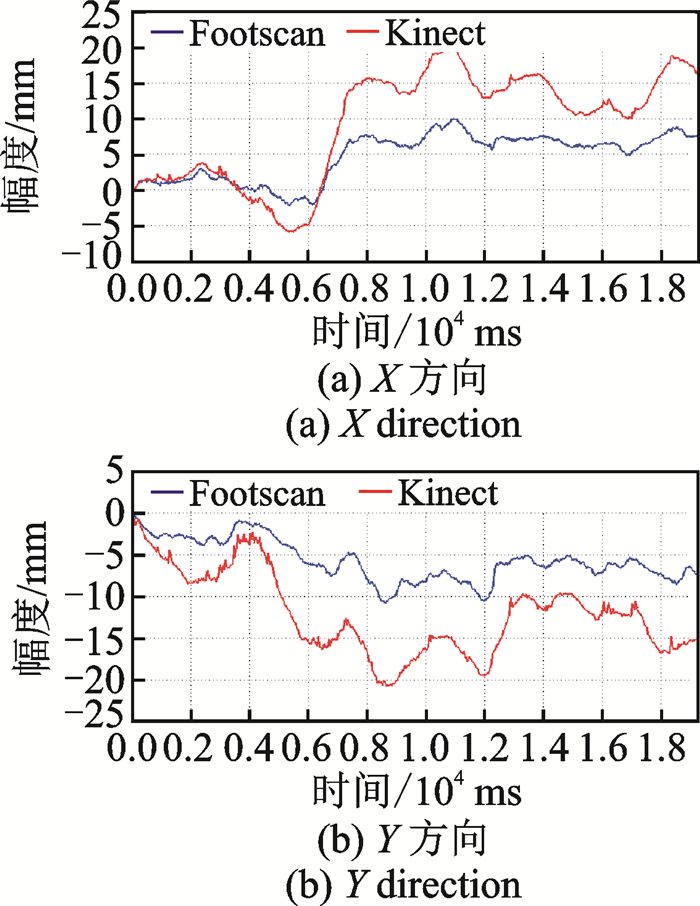
图 6 动作3的重心变化曲线 Fig. 6 Center of gravity change curve of action 3 |
从图中可以看出,两时间序列所绘制的图形整体走势趋于相似,但在部分区域存在较大差异。如图 4的(a, b), 两时间序列整体趋势相似,但在时间t∈[1.2×104 ms, 1.9×104 ms]时,Kt与Ft出现了较大差异,可能是由于Kinect对动作幅度较小的关节活动不敏感造成的,这一点在图 5(a)中同样可以看到,Kt的曲线要较Ft更平滑一些,但整体趋势仍然基本一致。可见Footscan提供的重心要比Kinect利用乘系数法求得的重心更敏感。由于动作2为身体前倾的动作,所以其Y方向的运动幅度要大于其X方向的运动幅度(约6倍)。
3组动作的的多个指标参数具体如表 2所示。从表 2可以看出,在静止状态和较小幅度动作变化的X方向上,基于Kinect的系统与平衡仪Footscan结果相比,均方根误差均小于7 mm,而在大幅动作和小幅动作的Y方向上,运动范围较大,均方根误差也较大,约33±3mm。虽然幅度较大的动作和方向上表现为较大的均方根误差,但是相对误差却较小,这与上述在静止性动作中的观察结果是吻合的,动作幅度虽小,相对误差却大。另外,从皮尔森相关系数(Pearson correlation coefficient)中可以看出,所有动作均呈现出线性正相关关系且相关系数较高,小幅动作X方向的相关系数0.5<r(0.7947)<0.8,具有显著相关性,其他动作相关系数r≥0.8具有高度相关性。
| 表 2 各动作参量 Tab. 2 Action parameters |
从前述分析看,本研究中的两时间序列(Kt,Ft)为同源信号,由不同设备采集得到,在进行协整检验之前,需首先对两个序列进行单位根检验,最常用的检验方法为增强单位根(Augmented Dickey-fuller, ADF)检验。若ADF检验结果表明两序列都是d(d>0)阶单整的,才可以继续进行协整关系判定。
对两个序列的原序列和一阶差分序列的单位根检验结果如表 3所示。由表 3可知,3组动作的Kt和Ft都是一阶单整序列,所以可以进一步检验其协整性。首先用OLS方法对Kt和Ft进行静态回归,并计算非均衡误差,即有
| $ {{\hat K}_t} = a{F_t} + b $ | (8) |
| $ {{\hat \mu }_t} = {K_t} - {{\hat K}_t} $ | (9) |
| 表 3 ADF单位根检验结果 Tab. 3 Test results of ADF unit root |
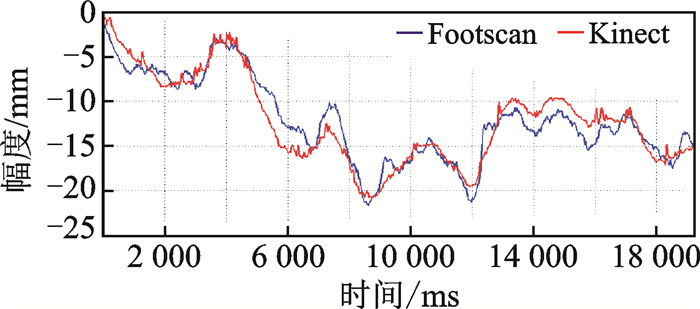
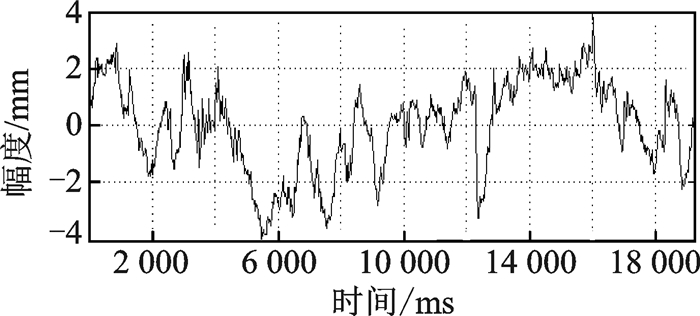
其中系数a,b的对应参数值可由OLS估计获得,具体结果如表 4所示。图 7为动作3在Y方向利用OLS拟合后的结果。使用ADF检验残差序列μt,结果如表 5所示。图 8为动作3在Y方向的残差序列。从结果可以看出,动作2在X方向的残差序列非平稳,即认为此处的Kt和Ft不具有协整关系,其他序列的判断结论均为平稳,即认为Kt和Ft具有协整关系。
|
图 7 动作3-Y方向拟合后的效果 Fig. 7 Effect of action 3-Y direction fitting |
|
图 8 动作3-Y方向的残差 Fig. 8 Residual error in action 3-Y direction |
| 表 4 利用OLS估计所得参数 Tab. 4 Parameters obtained from OLS |
| 表 5 残差序列ADF检验结果 Tab. 5 ADF test results of residual series |
如表 4, 5所示,当动作幅度减小时,参数a增大,到动作3的静止动作时,Kt约为Ft的2倍,造成这种现象的原因可能是Kinect对肢体末端(如手、脚跟和脚踝等)的识别精确度较低,在静止状态下,肢体末端关节点的识别误差被凸显了出来。可见,目前利用Kinect的乘系数法合成重心的方法更适合较大动作幅度时的重心轨迹测量。
4 结束语本研究利用Kinect提供的关节点位置信息通过乘系数法合成人体重心,并与Footscan平板压力测试系统提供的压力重心进行比较,发现该方法测量人体重心具有相似的结果,尤其在幅度较大的运动测量中,相对误差更小。在传统的乘系数法中,各方向的系数相同,并且X和Y方向的系数相差不大,由此认为仍可以使用该系数计算竖直方向的重心位置。
本文中使用的乘系数法作为一种计算量更小、更实时的重心计算方法,由于需要采用特定的人体模型降低了重心计算的精确性,同时由于Kinect自身以及硬件系统的局限性使人体部分关节点位置在某些情况下出现较大的误差,从而进一步影响了乘系数法的性能。下一步拟充分利用Kinect提供的25个关节点数据得出更个性化、更准确的系数。
| [1] |
Tan M, Nitz J, Boughen J, et al. Centre of gravity position in bipedal steady-stance is associated with performance of timed up and go but not functional reach[J]. Physiotherapy, 2015, 101(1): e1485-e1485. |
| [2] |
Boughen J, Nitz J, Johnston V. Centre of gravity:Relevance of behaviour and location in bipedal stance in older adults[J]. Physical Therapy Reviews, 2017, 22(3): 1-11. |
| [3] |
Crabolu M, Pani D, Raffo L, et al. Estimation of the center of rotation using wearable magneto-inertial sensors[J]. Journal of Biomechanics, 2016, 49(16): 3928. DOI:10.1016/j.jbiomech.2016.11.046 |
| [4] |
车保仁. 图象分析计算人体总重心的方法探讨[J]. 山东体育科技, 1985(2): 40-47. Che Baoren. Study on the method of calculating the total center of gravity of human body by image analysis[J]. Shandong Sport Science and Technology, 1985(2): 40-47. |
| [5] |
袁庆成. 计算身体重心的力矩合成法[J]. 冰雪运动, 1981(12): 72-74. Yuan Qingcheng. Torque synthesis for calculating the body's center of gravity[J]. China Winter Sports, 1981(12): 72-74. |
| [6] |
吴延禧. "乘系数法"人体重心计算公式[J]. 体育科技资料, 1980(18): 41-42. Wu Yanxi. "Multiply coefficient method" human body center of gravity calculation formula[J]. China Sport Science and Technology, 1980(18): 41-42. |
| [7] |
向泽锐, 支锦亦, 徐伯初, 等. 运动捕捉技术及其应用研究综述[J]. 计算机应用研究, 2013(8): 2241-2245. Xiang Zerui, Zhi Jinyi, Xu Bochu, et al. Survey on motion capture technique and its applications[J]. Application Research of Computers, 2013(8): 2241-2245. DOI:10.3969/j.issn.1001-3695.2013.08.001 |
| [8] |
Xiao J Z, Yang Z F, Wang H R, et al. Detection method of human three-dimensional body center of gravity based on inclinometer network[J]. Sensors & Materials, 2017, 29(7): 1081-1087. |
| [9] |
Corazza S, Andriacchi T P. Posturographic analysis through markerless motion capture without ground reaction forces measurement[J]. Journal of Biomechanics, 2009, 42(3): 370-374. DOI:10.1016/j.jbiomech.2008.11.019 |
| [10] |
Saeedkondori M. Estimation of the center of gravity of the human body using image processing[D]. USA: California State University, 2016.
|
| [11] |
Goude K, Pratt E, Davenport C, et al. Investigating the use of lower body and trunk kinematic data to calculate a clinically useful measure of centre of mass during gait[J]. Gait & Posture, 2014, 39: S103. |
| [12] |
段增武, 肖金壮, 王洪瑞. 基于Kinect的人体三维质心动态测量及准确性分析[J]. 中国生物医学工程学报, 2015(6): 752-756. Duan Zengwu, Xiao Jinzhuang, Wang Hongrui. The kinetic measurement and accuracy analysis of human body three-dimensional center of mass using Kinect[J]. Chinese Journal of Biomedical Engineering, 2015(6): 752-756. DOI:10.3969/j.issn.0258-8021.2015.06.016 |
| [13] |
Yang Y, Pu F, Li Y, et al. Reliability and validity of Kinect RGB-D sensor for assessing standing balance[J]. IEEE Sensors Journal, 2014, 14(5): 1633-1638. DOI:10.1109/JSEN.2013.2296509 |
| [14] |
Hasan S S, Robin D W, Szurkus D C, et al. Simultaneous measurement of body center of pressure and center of gravity during upright stance. Part Ⅰ:Methods[J]. Gait & Posture, 1996, 4(1): 1-10. |
| [15] |
Microsoft. Kinect hardware[EB/OL]. https://developer.microsoft.com/en-us/windows/kinect/hardware, 2016-05-31.
|
| [16] |
张克, 刘弘, 陆佃杰, 等. 基于单台Kinect的高精度个性化人体建模方法[J]. 数据采集与处理, 2015, 30(5): 1085-1090. Zhang Ke, Liu Hong, Lu Dianjie, et al. Personalized human body modeling with high precision based on single Kinect[J]. Journal of Data Acquisition and Processing, 2015, 30(5): 1085-1090. |
 2018, Vol. 33
2018, Vol. 33


