雷达作为一种重要的电磁传感器, 在国防和民用领域发挥着越来越重要的作用。在应用需求的牵引和技术发展的推动下, 当前雷达技术的发展日新月异, 一些新体制、新系统和新方法不断涌现。多输入多输出(Multiple input multiple ontput, MIMO)雷达就是把无线通信系统中的多个输入和多个输出技术引入到雷达领域, 并和数字阵列技术相结合而产生的一种新体制雷达[1-20]。
MIMO雷达的概念在2003年由美国林肯实验室的Bliss和Forsythe首次提出[1], 目前已成为国内外雷达界的一个研究热点。在MIMO雷达定义中, 多输入是指同时发射多种雷达信号波形(一般是多个天线同时发射不同的波形), 多输出是指多个天线同时接收并通过多路接收机输出以获得多通道空间采样信号。在这一概念框架下, 传统的机械扫描雷达由于只发射一种信号波形, 也只有一路接收机输出, 其属于单输入单输出雷达; 单脉冲雷达只发射一种信号波形, 一般有两路(和波束与差波束或者左波束和右波束)接收机输出, 其属于单输入双输出雷达; 相控阵数字波束形成(Digital beamforming, DBF)体制雷达多个发射天线同时发射相同波形的信号, 多个接收天线也同时接收信号并经多路接收机输出, 它可以看作单输入多输出雷达。根据发射和接收天线中各单元的间距大小, 可以将MIMO雷达分为分布式MIMO雷达(又称统计MIMO雷达或非相干MIMO雷达)[2]和集中式MIMO雷达(又称相干MIMO雷达)[3]两类。分布式MIMO雷达中收发天线各单元相距很远, 使得各阵元可以分别从不同的视角观察目标, 从而获得空间分集得益, 克服目标雷达截面积(Radar cross section, RCS)的闪烁效应, 提高雷达对目标的探测性能。而集中式MIMO雷达的收发天线各单元相距较近, 各个天线单元对目标的视角近似相同, 且每个阵元可以发射不同的信号波形, 从而获得波形分集, 使得集中式MIMO雷达具有虚拟孔径扩展能力及更灵活的功率分配能力, 改善系统的能量利用率、测角精度、杂波抑制及低截获能力等性能。需要说明的是, 虽然分布式MIMO雷达强调的是空间分集得益, 但是其各发射单元的波形也是不同的(通常是相互正交的), 即也是波形分集的。自从MIMO雷达的概念提出后, 迅速成为雷达领域关注的热点, 每年的国际会议和期刊都有不少关于MIMO雷达的研究成果发表。目前, 行业内对MIMO雷达的认识褒贬不一, 迫切需要对MIMO雷达有一个全面、正确的认识和评价, 基于该目的, 本文作者在对MIMO雷达多年研究的基础上, 从理论研究和工程应用相结合的角度出发, 对MIMO雷达的基本原理、特点、研究现状及应用等方面进行综述。
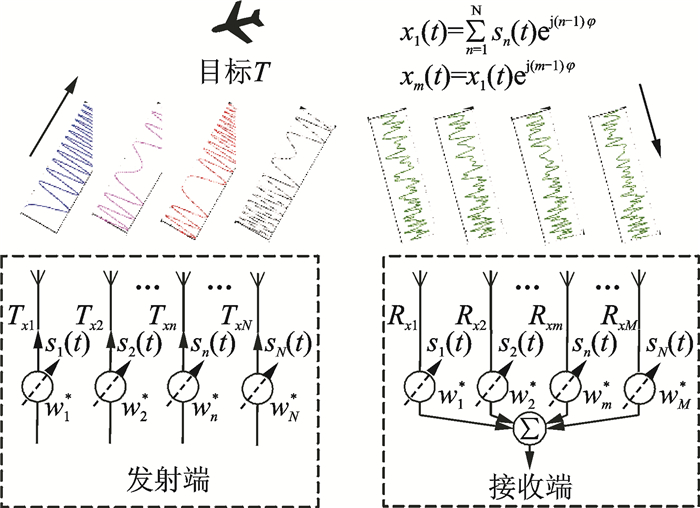
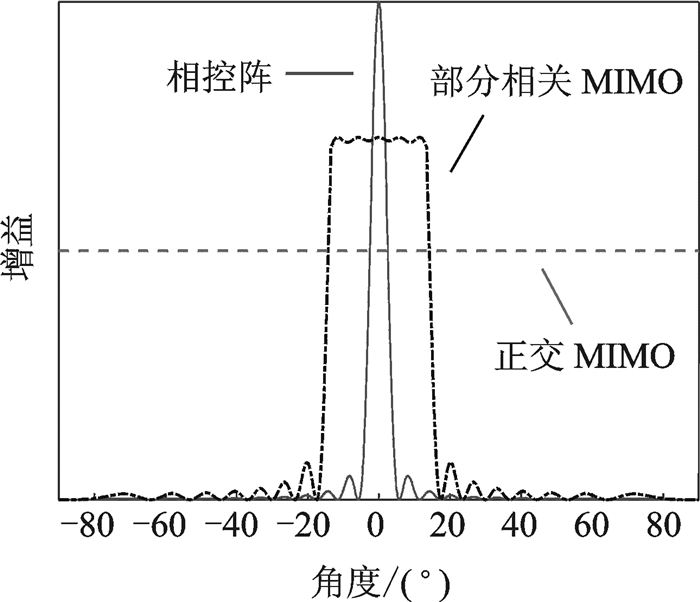
1 MIMO雷达原理 1.1 MIMO雷达基本组成MIMO雷达通常包含多个发射天线和多个接收天线(天线也可以收发共用), 各发射天线发射不同的信号波形, 各发射信号经过目标反射后被多个接收天线接收, 并经过多路接收机后送给信号处理进行后续处理, MIMO雷达的组成框图如图 1所示。在MIMO雷达系统中各阵元各发射信号不再是一组相干信号, 而是一组相互正交或部分相关信号。此时各信号在空间叠加后不会形成高增益的窄波束, 而是会形成低增益的宽波束, 对较大的空域范围同时实现能量覆盖, 从而实现对大空域范围内的目标同时进行跟踪和搜索。如图 2所示, 当MIMO雷达各发射信号相互正交时, 则其发射能量覆盖没有方向性(假设单个天线单元没有方向性), 在所有方向增益相同; 当各发射信号部分相关时, 则其发射能量覆盖为低增益的宽波束, 波束指向和波束宽度由发射信号波形及其相位决定; 当各发射信号完全相关(即相干)时, 则其发射能量覆盖为高增益的窄波束, 波束指向由发射信号相位决定, 此时等效于各发射信号完全相同, 只是相位不同, 这时就变成了常规的相控阵雷达(更准确地说是数字阵列雷达)。
|
图 1 MIMO雷达基本组成 Fig. 1 Configuration of MIMO radar |
|
图 2 MIMO雷达不同发射信号时的发射能量覆盖图 Fig. 2 Transmit energy distribution of MIMO radar for different transmit waveforms |
1.2 MIMO雷达信号处理流程
众所周知, 信号处理是雷达系统的核心部分, MIMO雷达的最大特点是其采用了波形分集技术, 在接收端首先对目标反射的各发射信号进行分离, 再经过相位补偿后合成, 完成发射波束形成, 接收天线之间再进行接收数字波束形成, 从而同时获得了发射和接收天线增益。可以看出, MIMO雷达的发射波束形成和接收波束形成都是在接收端的信号处理中实现, 所以MIMO雷达的基本原理主要体现在信号处理中。下面给出MIMO雷达的信号处理流程。
假设共有N个发射天线和M个接收天线, si(n)为第i个发射天线发射信号包络(脉冲)的离散时间采样, 设发射信号包络共有L个离散时间采样, 则
| $ {\mathit{\boldsymbol{R}}_s} = \frac{1}{L}\sum\limits_{n = 1}^L \mathit{\boldsymbol{s}} \left( n \right)\mathit{\boldsymbol{s}}{^{\rm{H}}}\left( n \right) = {\mathit{\boldsymbol{I}}_N} $ | (1) |
其中IN为N×N的单位阵。设ar(θ)和at(θ)分别为对应于方向θ的接收阵列导向矢量和发射阵列导向矢量, 整个接收天线阵列接收到的信号表示为
| $ \mathit{\boldsymbol{y}}\left( n \right) = {\left[{{y_1}\left( n \right), {y_2}\left( n \right), \ldots, {y_M}\left( n \right)} \right]^{\rm{T}}} $ | (2) |
其中yi(n)为第i个接收天线接收到的信号。设在方向θ0处有一个目标, 则有
| $ \mathit{\boldsymbol{y}}\left( n \right) = \beta {\mathit{\boldsymbol{a}}_{\rm{r}}}\left( {{\theta _{0}}} \right){\mathit{\boldsymbol{a}}_t}^{\rm{T}}\left( {{\theta _{0}}} \right)\mathit{\boldsymbol{s}}\left( n \right) + \mathit{\boldsymbol{w}}\left( n \right) $ | (3) |
其中β为目标回波幅度, w(n)为噪声, 式中忽略了由目标距离引起的信号延迟。
在MIMO雷达信号处理中, 可以根据发射波束形成放置的不同位置采用不同的处理流程。目前主要有两种处理流程:(1)处理流程是把发射波束形成与接收波束形成联合实现; (2)处理流程是把发射波束形成与脉冲压缩联合实现。
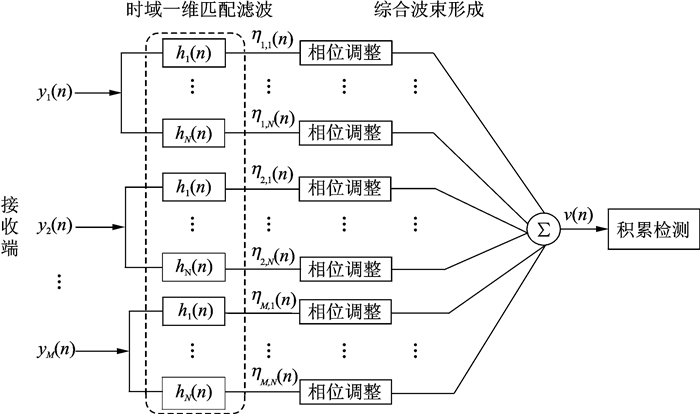
1.2.1 第1种处理流程该处理流程主要包括时域一维匹配滤波和综合波束形成, 如图 3所示。其中时域一维匹配滤波实现脉冲压缩和各发射信号分离作用, 综合波束形成是指对所有路接收信号的全部时域一维匹配滤波器的输出进行调相求和处理, 使其能进行有效合成, 等效于同时实现接收波束形成和发射波束形成功能, 波束形成的输出再进行和常规雷达相同的脉冲积累、检测等处理。所有路接收信号的全部时域一维匹配滤波器的输出排列成一个向量时就等效于发射和接收阵列联合形成的一个虚拟天线阵列, 综合波束形成即是对虚拟天线阵列信号进行的波束形成操作。N个时域滤波器分别与N个发射信号相匹配, 所以第i个时域滤波器的权系数为
| $ {\mathit{\boldsymbol{h}}_i}\left( n \right) = {{\mathit{\boldsymbol{\bar s}}}_i}\left( {N-n} \right)\;\;\;\;\;\;\;\;\;i = 1, \ldots, N $ | (4) |
|
图 3 MIMO雷达第1种信号处理流程 Fig. 3 The first signal processing flow of MIMO radar |
式中:上划线表示复数共轭, 该滤波器只和时间有关, 而与方向无关。由于N个发射信号相互正交, 上述滤波器在实现匹配滤波的同时, 也起到了对目标反射的各发射信号进行分离的作用, 例如第i个时域滤波器在正好和第i个发射信号匹配的时刻, 对其他发射信号的滤波输出等于0, 这很容易根据式(1)得到。
1.2.2 第2种处理流程该处理流程主要包括接收波束形成和脉冲综合, 如图 4所示。其中脉冲综合同时实现脉冲压缩和发射波束形成功能。为了对θ0方向的目标进行脉冲综合, 则脉冲综合要θ0方向的目标回波匹配, 其权系数为对θ0方向的目标回波进行倒序并取共轭, 有
| $ \mathit{\boldsymbol{h}}\left( n \right) = {\mathit{\boldsymbol{a}}_{t}}^{\rm{H}}({\theta _{0}})\mathit{\boldsymbol{\bar s}}\left( {N-n} \right) $ | (5) |

|
图 4 MIMO雷达第2种信号处理流程 Fig. 4 The second signal processing flow of MIMO radar |
可以看出, 脉冲综合不仅和时间有关, 还和方向有关, 所以其匹配滤波又称为时空两维匹配滤波(其中时间一维, 方向一维), 脉冲综合等效于实现了对某方向目标反射的发射信号的匹配滤波, 而和接收阵列没有关系, 如果对不同方向的目标进行匹配滤波, 则其脉冲综合权系数不同。而常规相控阵雷达中的脉冲压缩也是匹配滤波, 但是其权系数和目标方向无关, 这是MIMO雷达与常规相控阵雷达的不同之处。
1.2.3 两种处理流程的关系虽然上述两种处理流程看似有所不同, 其实质主要是各部分的先后次序不同, 可以证明两者是完全等价的, 且在通常情况下第2种流程的运算量要远小于第1种的运算量[4], 但是第2种流程中脉冲综合的权系数与方向有关, 当同时形成多个方向的波束时权系数较多, 需要的存贮量大。需要说明的是, 第1种处理流程是MIMO雷达默认的处理流程, 通过该流程也很容易对MIMO雷达形成的虚拟天线孔径和孔径扩展进行解释, 但是图 3中的处理流程只适用于正交波形的情况, 当发射波形非完全正交而是部分相关时, 该处理流程需要对时域滤波器的个数和其权系数进行相应的修改[5]。第2种处理流程则对正交和部分相关波形都适用。
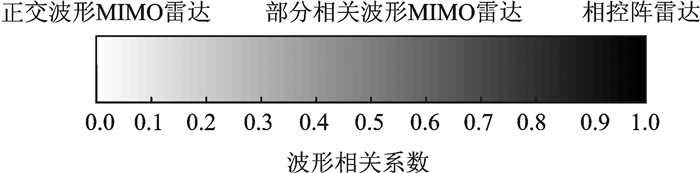
1.3 MIMO雷达与相控阵雷达的关系MIMO雷达的最大特点是采用了波形分集技术, 表示波形分集的一个重要参数就是波形的相关系数, 当波形相关系数是0时代表波形相互正交, 这就是正交波形MIMO雷达, 当波形相关系数是1时代表波形相干(即波形完全相同), 这就是相控阵雷达, 当波形相关系数是介于0和1之间时代表波形部分相关, 这就是部分相关波形MIMO雷达, 不同波形相关系数时的雷达类别如图 5所示。
|
图 5 不同波形相关系数时的雷达类别 Fig. 5 Category of radar for different correlation coefficient of waveforms |
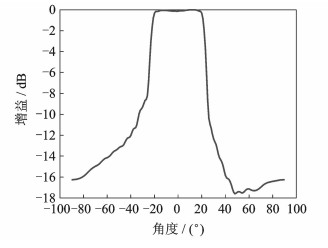
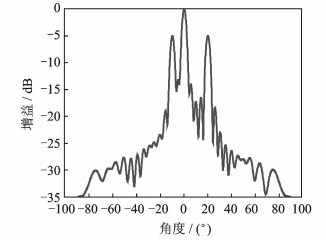
需要说明的是, 如果把MIMO雷达定义为波形分集雷达的话, 正交波形只是波形分集的一个特例, 也是目前大家通常默认的MIMO雷达, 实际上还存在大量的部分相关波形MIMO雷达。通常认为部分相关波形MIMO雷达指的是阵元级波形部分相关, 后来又出现了子阵正交MIMO雷达的概念[6-10], 其实也算是部分相关波形MIMO雷达的1种, 只不过子阵正交MIMO雷达可以借鉴现有的正交波形设计结果, 其得到的发射能量覆盖图是一个宽波束, 其波束宽度由子阵的阵元个数确定, 而阵元级波形部分相关MIMO雷达则更灵活, 通过波形设计其不仅可以得到宽波束的发射能量覆盖图(一般搜索时使用), 如图 6所示, 也能得到同时多个独立窄波束的发射能量覆盖图, 且各波束的增益可以不同(一般搜索并跟踪或者同时跟踪多个目标时使用), 如图 7所示。
|
图 6 宽波束发射能量覆盖图 Fig. 6 Transmit energy distribution for wide beam |
|
图 7 同时多个窄波束发射能量覆盖图 Fig. 7 Transmit energy distribution for multibeams |
既然MIMO雷达的平台可以产生波形分集, 其也可以产生完全相同的波形, 所以MIMO雷达应该是相控阵雷达的一个扩展(即波形由完全相同扩展到波形不同), 相控阵雷达则是MIMO雷达的一个特例, 或者说MIMO雷达可以完全兼容相控阵雷达, 因为其平台完全可以根据波形设置工作在相控阵雷达模式上。其实当MIMO雷达工作在相控阵模式时, 其完全变成了一个数字阵列雷达, 数字阵列雷达的基本原理与相控阵雷达相同, 只不过是每个发射天线阵元都对应一个波形产生器, 每个波形产生器都产生波形相同初相不同的波形, 等效于用多个波形产生器代替了相控阵雷达中的移相器, 其实多个波形产生器完全可以产生多个不同的波形, 故从此角度说, 数字阵列雷达没有充分利用平台存在的资源。需要强调的是, MIMO雷达通常发射宽波束或者同时多个独立波束, 这时其接收波束的覆盖也需要和发射波束能量覆盖相同, 因此其往往需要同时形成多个接收波束, 所以MIMO雷达一定是DBF体制的系统。
2 MIMO雷达特点由MIMO雷达的基本原理可知, 其各发射天线发射的波形可以独立控制, 可以根据不同应用场景来实现同时满足距离—速度分辨要求的时域波形和空间能量分布要求的发射方向图, 在接收端通过综合利用发射波形特性及接收空域自由度来获得良好的探测性能。相对于相控阵雷达, 其主要优势在于:
(1) 工作模式灵活。相控阵雷达是通过控制发射信号相位来实现发射信号的空间功率合成。MIMO雷达可以控制多个发射通道的发射信号波形, 其可控自由度更多。MIMO雷达多个发射通道可以像相控阵雷达一样发射相同的信号波形, 形成一个窄的发射波束; 也可以发射完全正交的信号波形, 形成全空域、全向发射方向图; 也可以根据要求发射相关的信号波形, 形成同时多个方向发射或展宽的赋形方向图。窄波束发射可以用于单目标跟踪, 全向或宽波束发射可用于目标搜索, 多方向发射可以用于多目标同时跟踪。其带来的显著优势是可以综合利用发射波形来解决时间和能量资源的矛盾, 在多功能雷达中有广阔的应用前景。
(2) 测角精度高。由前面的MIMO雷达第一种处理流程知道, 通过波形分集可以得到虚拟天线孔径, 实现天线孔径的扩展, 从而提高测角精度。其实质是MIMO雷达测角可以联合使用发射和接收天线两端处理, 而传统的相控阵雷达只能使用天线接收端处理, 其测角精度只和接收天线孔径有关, 所以孔径扩展的定义应该是虚拟天线孔径和接收天线孔径的比值再减去1。MIMO雷达测角精度的提高或者天线孔径的扩展和以下两个因素有关:
(a) 收发天线位置
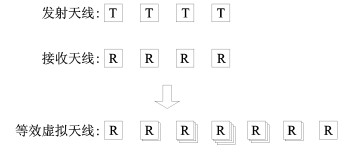
不同的天线收发位置得到的虚拟天线孔径不同, 所带来的天线孔径扩展也不同。如图 8和图 9分别为正交波形MIMO雷达2发4收和4发4收的天线孔径扩展示意图。可以看出, 图 8的天线孔径扩展为1倍, 其测角精度也会提高1倍, 图 9的天线孔径扩展看似接近1倍, 其实其为大约40%, 因为虚拟天线阵列的中间阵元幅度较大(由较多的阵元合成)、两边阵元幅度较小(由较少的阵元合成), 等效于进行了幅度加权, 其孔径会有一定损失, 所以该收发结构的正交MIMO雷达测角精度大约提升40%, 这种结构是一般雷达天线中常用的收发天线共用等间距线阵结构, 这也正是人们常说的MIMO雷达测角精度会提升40%的根源。

|
图 8 正交波形MIMO雷达2发4收天线孔径扩展示意图 Fig. 8 Virtual array aperture for MIMO radar transmitting orthogonal waveforms(2 transmit antennas and 4 receive antennas) |
|
图 9 正交波形MIMO雷达4发4收的天线孔径扩展示意图 Fig. 9 Virtual array aperture for MIMO radar transmitting orthogonal waveforms (4 transmit antennas and 4 receive antennas) |
(b) 发射波形的相关系数
理论研究表明[11], 在其他条件都相同的条件下, MIMO雷达的测角精度随着其发射波形的相关系数改变而变化, 在正交波形时其测角精度最高, 等效于天线孔径扩展最大, 随着波形相关系数的增加, 测角精度会下降, 在波形完全相关(即相干, 也就是常规的相控阵雷达)时, 测角精度最低, 等效于没有天线孔径扩展。有关部分相关波形MIMO雷达的天线孔径扩展不太好直接给出类似于正交波形时孔径扩展的物理解释, 不过可以结合子阵正交MIMO雷达进行类似的物理解释。
(3) 杂波抑制能力强, 多普勒频率分辨率高。强杂波背景下的目标探测是雷达技术面临的重要课题。获得良好的杂波抑制性能的基础是长的波束驻留时间。传统的窄波束发射体制受搜索空域、多目标跟踪等因素限制, 波束驻留时间有限, 杂波抑制性能难以提高。MIMO雷达可以通过宽波束或同时多个窄波束发射, 在保证搜索或跟踪数据率条件下增加波束驻留时间, 提升杂波抑制能力和多普勒频率分辨率, 在强杂波背景下慢速目标探测方面具有良好应用前景。
(4) 数据率高。MIMO雷达在正交发射波形模式下, 可以通过同时多波束接收实现长时间波束驻留, 在保证搜索空域和探测威力的条件下可以通过滑窗处理获得更高的数据率, 可以显著提升雷达对机动目标跟踪性能。
(5) 多目标跟踪能力强。传统相控阵雷达对多目标跟踪是分时实现, MIMO雷达可以实现同时多目标跟踪, 即同时发射多个窄波束, 在不同目标方向上根据需要配置发射增益, 且各个发射波束方向的时域波形可以实现正交, 可以有效解决多目标跟踪中的资源配置、跟踪精度和时间能量冲突等问题。
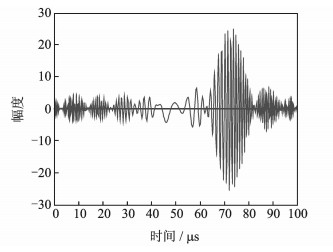
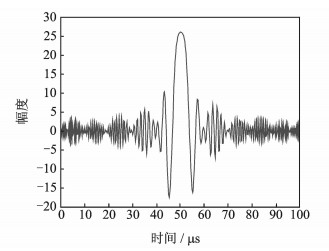
(6) 抗干扰能力强。传统相控阵雷达发射的波形各向同性, 即各个方向上的时域波形相同。MIMO雷达各发射天线的时域波形不同, 因此在不同方向上空间合成的时域波形各不相同。对方的干扰机在副瓣方向采用储频转发方式进行欺骗式干扰, 干扰信号和主瓣方向上的目标回波波形不同, 通过匹配滤波处理以后对干扰具有一定的抑制作用。如果采用被动定位方法来对MIMO雷达进行定位, 由于MIMO雷达不同方向上的发射信号是不同的, 对其进行定位较为困难。因此, MIMO雷达具有更强的抗侦察定位和抗干扰的能力。图 10~12分别为同一MIMO雷达在方向为-10°, 0°和20°处的合成信号, 可以看出三者的现状差别很大。
|
图 10 MIMO雷达-10°方向时域波形 Fig. 10 Synthetic waveform for MIMO radar in -10° |
|
图 11 MIMO雷达0°方向时域波形 Fig. 11 Synthetic waveform for MIMO radar in 0° |

|
图 12 MIMO雷达20°方向时域波形 Fig. 12 Synthetic waveform for MIMO radar in 20° |
(7) 能量利用率高。雷达在对信号进行接收时, 仅对期望探测空域范围内的回波信号进行接收, 而范围外的回波信号被认为是干扰。因此可以认为仅落在接收空域范围内的发射能量有效, 而副瓣内的能量都被浪费了。传统相控阵雷达往往发射高增益窄波束, 当需要对大空域范围进行搜索时, 需要分时进行, 这样就存在多次副瓣能量浪费。而MIMO雷达通过对发射波形设计可以发射宽波束同时对大空域范围进行同时搜索, 副瓣能量浪费少, 因此具有更高的能量利用率。尤其是天线阵列是稀布阵列时, 波束的副瓣大, 能量浪费更严重, MIMO雷达的优势更明显。MIMO雷达和相控阵雷达比, 其主要不足之处如下:
(a) 运算量大。由于MIMO雷达往往同时形成的波束数目多, 且波束驻留时间长, 积累时间长, 运算量大。
(b) 不适合做单目标跟踪。MIMO雷达发射能量覆盖宽度宽, 增益有损失, 在进行单目标跟踪时只有目标方向附近的发射波束能量有用, 其他地方的能量没有用, 造成发射波束能量浪费严重, 不适合做单目标跟踪使用。
(c) 脉冲综合距离副瓣高, 容易带来目标之间的互相影响。把脉冲压缩变成了时空匹配滤波处理, 其输出距离副瓣高, 且不能通过加窗的方法降低距离副瓣, 会造成距离不同但是速度相同的目标之间的影响, 尤其是大目标距离副瓣会对小目标检测有影响。
(d) 目前研究的波形对多普勒频率敏感, 不利于高速目标探测。由于MIMO雷达采用波形分集技术, 为了设计MIMO雷达波形方便, 目前大都采用相位编码波形, 这会把相位编码波形的固有缺陷带进来, 即波形对多普勒频率敏感, 尤其是波形时宽宽或目标速度较高时。
3 MIMO雷达研究现状MIMO雷达的概念于2003年被美国林肯实验室提出后, 其迅速成为了雷达领域研究的热点, 每年的国际会议和期刊都有不少关于MIMO雷达的论文发表[2-33]。在2009年, Li J出版了一本《MIMO雷达信号处理》的专著[3], 在2006年, Bekkerman等结合阵列信号处理技术对MIMO雷达的性能进行了深入的分析[5], 在2004年美国林肯实验室公布了该实验室设计的L波段和X波段两个MIMO雷达实验系统的实验结果[12], 在2007年Li J等发表了一篇关于MIMO雷达的综述性文章[13], 对比了MIMO雷达和常规相控阵列雷达的性能, 。在最近几年的会议和期刊上都有大量MIMO雷达的论文发表。目前国际上对MIMO雷达的研究热度有增无减。在如ICASSP, Asilomar和雷达会议等许多著名的国际会议中, 都设有MIMO雷达的专场讨论会。
根据现有的研究状况分析, 国内外雷达学者对MIMO雷达的研究主要分为两个方面:(1)MIMO雷达自身技术方面, 主要从系统总体(包含子阵正交MIMO雷达)、波形设计、信号处理、参数估计以及阵列误差校正等方面对其进行了广泛的研究[14-23]; (2)结合具体应用背景的MIMO雷达相关技术方面, 主要包含MIMO-SAR、MIMO-STAP、双基地MIMO雷达(主要是DOD和DOA估计)以及天波MIMO雷达等[24-30]。目前国内外对MIMO雷达的研究存在“五多五少”的特点:(1)理论问题研究得多, 实际工程应用问题研究得少; (2)正交波形研究得多, 部分相关波形研究得少; (3)相位编码波形研究得多, 其他编码波形研究得少; (4)一维线阵研究得多, 二维平面阵研究得少; (5)优点讨论得多, 缺点讨论得少。在2009年的IEEE AES Magazine期刊上[31], 雷声公司发出了不同的声音, 他们从工程角度指出关于MIMO雷达的现有研究成果大部分是无用的, 这也从侧面反映了目前对MIMO雷达的研究太专注理论而与实际应用脱节的现状。
虽然MIMO雷达的概念是近几年才提出的, 但在此之前国际上早已有对这类技术的研究, 例如在20世纪70年代末法国国家宇航研究局与汤姆逊-CSF公司研制的综合脉冲与孔径雷达(Synthetic impulse and aperture radar, SIAR)就是采用了MIMO雷达的这种多输入多输出思想[34], 并在实验系统上得到验证。该雷达采用正交波形MIMO的思想, 稀布圆形阵列的发射天线设计, 通过各个阵元能全向发射正交的频率编码信号, 以实现各个天线单元对空间的全向照射, 在接收端通过直达波与目标回波进行相关接收, 实现对发射信号的综合脉冲处理, 以形成相干接收与发射波束。
4 MIMO雷达应用前景及技术发展分析MIMO雷达的理论研究已有较好的研究基础, 结合具体应用背景开展MIMO雷达的应用研究是目前需要研究的重点。根据前面的讨论可知, MIMO雷达的实现平台就是数字阵列雷达, 所以目前MIMO雷达已经完全具备了良好的工程应用条件。
4.1 MIMO雷达应用前景分析和相控阵雷达相比, MIMO雷达并不全是优势, 也有它的劣势, 在工程应用时应该把它用到适当的场合, 使其“扬长避短”。根据前面对MIMO雷达的优劣势分析, MIMO雷达在以下几个方面具有良好的应用前景:
(1) 在天线孔径有限情况下希望尽量提高测角精度的雷达系统。米波雷达和天波(地波)超视距雷达由于波长长, 天线孔径有限, 波束宽, 测角精度差, 如果采用MIMO雷达体制可以在相同的天线孔径条件下进一步提升测角精度; 机载预警雷达可以在相同的天线垂直孔径条件下进一步提高测高精度。
(2) 能够充分利用MIMO雷达可控自由度多的雷达系统。天波超视距雷达可以利用MIMO雷达收发联合处理自由度多的特点, 通过自适应波束形成(尤其是发射端的波束形成)抑制其他电离层折射回波对目标检测的影响; 机载预警雷达可以利用收发联合自适应处理提升杂波抑制性能; 多功能雷达和认知雷达可以充分利用MIMO雷达发射端多自由度可控形成需要的发射波束覆盖提升雷达系统性能[35]。
(3) 低空探测和低慢小目标探测雷达系统, 可以根据需要通过发射波形设计得到适当宽度的发射波束覆盖, 增加脉冲积累时间, 提高杂波抑制性能和对目标的多普勒频率分辨率, 从而提升雷达的低空检测和对低慢小目标探测性能。需要说明的是, 对于相控阵雷达来说, 也可以通过相位加权得到宽的发射波束覆盖, 同样具有良好的低空探测和低慢小目标探测, 但是采用MIMO雷达体制会获得更高的测角精度且具有更强的抗侦察性能。
(4) 天线采用稀布阵列的雷达系统。这时采用MIMO雷达体制, 其能量利用率更高。
4.2 MIMO雷达下一步技术发展分析目前MIMO雷达已经完全具备了良好的工程应用条件, 下一步的发展除了本身理论的进一步完善之外, 应该以克服在实际工程应用中的问题为主, 主要包含以下几个方面:
(1) 部分相关波形MIMO雷达相关理论和信号处理方法的进一步完善。其实部分相关波形MIMO雷达应该是在实际应用中的大部分情况, 正交波形MIMO雷达只是少数情况, 而对于部分相关波形MIMO雷达的有关理论分析和信号处理方法还有待于进一步细化和深入。
(2) 双基地MIMO雷达的工程应用问题。目前对双基地MIMO雷达的研究主要是测角方面, 即DOD和DOA估计, 但是DOD和DOA估计出来之后怎么应用方面还没有相关的研究, 且双基地雷达采用MIMO体制时会急剧增加处理和检测的运算量, 这个问题也需要解决。
(3) MIMO雷达快速发射波形优化设计。在认知雷达和多功能雷达系统中, 发射波束覆盖往往需要根据跟踪目标情况实时调整, 这就需要快速实时设计发射波形, 这方面是MIMO雷达下一步研究的一个重点方向。
(4) 对多普勒频率稳健的MIMO雷达波形设计。目前MIMO雷达的波形大都采用相位编码波形, 该波形对多普勒频率敏感, 尤其是波形时宽宽或目标速度较高时, 所以开展对多普勒频率稳健的MIMO雷达波形设计也是一个重要研究方向。
(5) 低复杂度信号处理算法。由于MIMO雷达往往同时形成的波束数目多, 且波束驻留时间长, 积累时间长, 运算量大, 需要一些快速的信号处理算法。目前的信号处理器件发展日新月异, 其计算能力在不停地快速提升, 这为MIMO雷达工程应用提供了有利的条件。
5 结束语MIMO雷达是基于数字阵列雷达平台并采用波形分集的一种新体制雷达, 是相控阵雷达的扩展, 具有可控自由度多、发射波束设置灵活、测角精度高以及抗干扰能力强等优点, 在军事和民用领域都有着广阔的应用前景, 是雷达下一步发展的重要方向。经过十几年的研究, MIMO雷达目前已进入工程实用阶段。但是作为一种新型的雷达体制, 其应用仍需要大力推进, 其性能也值得深入挖掘。
| [1] |
Bliss D W, Forsythe K W. Multiple-input multiple-output (MIMO) radar and imaging: Degrees of freedom and resolution[C]//Proc 37th Asilomar Conf Signals, Syst Comput. Pacific Grove, CA: [s. n. ], 2003: 54-59.
|
| [2] |
Haimovich A M. MIMO radar with widely separated antennas[J]. IEEE Signal Processing Magazine, 2008, 25(1): 116-129. DOI:10.1109/MSP.2008.4408448 |
| [3] |
Li J, Stoica P. MIMO radar signal processing[M]. New York: John Wiley & Sons, Inc., 2009.
|
| [4] |
赵永波, 董玫, 张守宏. MIMO雷达的信号处理方法研究[J]. 航空计算技术, 2009, 39(3): 103-106. Zhao Yongbo, Dong Mei, Zhang Shouhong. Study on signal processing in MIMO radar[J]. Aeronautical Computing Technique, 2009, 39(3): 103-106. |
| [5] |
Bekkerman I, Tabrikian J. Target detection and localization using MIMO radars and sonars[J]. IEEE Trans Signal Processing, 2006, 54(10): 3873-3883. DOI:10.1109/TSP.2006.879267 |
| [6] |
Friedlander B. On the relationship between MIMO and SIMO radars[J]. IEEE Trans Signal Processing, 2009, 57(1): 394-398. DOI:10.1109/TSP.2008.2007106 |
| [7] |
He Q. Cramer-rao bound for MIMO radar target localization with phase errors[J]. IEEE Signal Processing Letters, 2010, 17(1): 83-86. DOI:10.1109/LSP.2009.2032994 |
| [8] |
Hassanien A. Phased-MIMO radar:A tradeoff between phased-array and MIMO radars[J]. IEEE Trans on Signal Process, 2010, 58(6): 3137-3151. DOI:10.1109/TSP.2010.2043976 |
| [9] |
Hassanien A. Transmit energy focusing for DOA estimation in MIMO radar with colocated antennas[J]. IEEE Trans on Signal Process, 2011, 59(6): 2669-2682. DOI:10.1109/TSP.2011.2125960 |
| [10] |
Wilcox D, Sellathurai M. On MIMO radar subarrayed transmit beamforming[J]. IEEE Trans Signal Processing, 2012, 60(4): 2076-2081. DOI:10.1109/TSP.2011.2179540 |
| [11] |
程增飞, 赵永波, 李慧, 等. 部分相关MIMO雷达比幅单脉冲测角性能分析[J]. 系统工程与电子技术, 2017, 39(9): 1979-1984. Cheng Zengfei, Zhao Yongbo, Li Hui, et al. Angle estimation performance analysis of amplitude comparison mono-pulse for partially correlated MIMO radar[J]. System Engineering and Electronics, 2017, 39(9): 1979-1984. DOI:10.3969/j.issn.1001-506X.2017.09.10 |
| [12] |
Robey F C. MIMO radar theory and exprimental results[C]//Proc 38th Asilomar Conf Signals Syst Comput. Pacific Grove, CA: [s. n. ], 2004: 300-304.
|
| [13] |
Li J, Stoica P. MIMO radar with collocated antennas[J]. IEEE Signal Processing Magazine, 2007, 24(5): 106-114. DOI:10.1109/MSP.2007.904812 |
| [14] |
Stoica P, Li J, Xie Y. On probing signal design for MIMO radar[J]. IEEE Trans Signal Processing, 2007, 55(8): 4151-4161. DOI:10.1109/TSP.2007.894398 |
| [15] |
Friedlander B. Waveform design for MIMO radars[J]. IEEE Trans Aerospace and Electronic Systems, 2007, 43(3): 1227-1238. DOI:10.1109/TAES.2007.4383615 |
| [16] |
Maio A D, Lops M. Design principles of MIMO radar detectors[J]. IEEE Trans Aerospace and Electronic Systems, 2007, 43(3): 886-898. DOI:10.1109/TAES.2007.4383581 |
| [17] |
Friedlander B. Effects of model mismatch in MIMO radar[J]. IEEE Transactions on Signal Processing, 2012, 60(4): 2071-2076. DOI:10.1109/TSP.2011.2179653 |
| [18] |
Huleihel W, Tabrikian J, Shavit R. Optimal adaptive waveform design for cognitive MIMO radar[J]. IEEE Trans Signal Processing, 2013, 61(20): 5075-5089. DOI:10.1109/TSP.2013.2269045 |
| [19] |
Rabideau D J. MIMO radar waveforms and cancellation ratio[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(2): 1167-1178. DOI:10.1109/TAES.2012.6178055 |
| [20] |
Babur G, Krasnov O A, Yarovoy A, et al. Nearly orthogonal waveforms for MIMO FMCW radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2013, 49(3): 1426-1437. DOI:10.1109/TAES.2013.6557996 |
| [21] |
Friedlander B. On transmit beamforming for MIMO radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2012, 48(4): 3376-3388. DOI:10.1109/TAES.2012.6324717 |
| [22] |
Deng H. Polyphase code design for orthogonal netted radar systems[J]. IEEE Trans Signal Processing, 2004, 52(11): 3126-3135. DOI:10.1109/TSP.2004.836530 |
| [23] |
Qiu Z K, Yang J, Chen H W, et al. Effects of transmitting correlated waveforms for co-located multi-input multi-output radar with target detection and localization[J]. IET Signal Process, 2013, 7(9): 897-910. DOI:10.1049/iet-spr.2012.0323 |
| [24] |
Mecca V F, Ramakrishnan D, Krolik J L. MIMO radar space-time adaptive processing for multipath clutter mitigation[C]//Fourth IEEE Sensor Array and Multichannel Signal Processing Workshop. [S. l. ]: IEEE, 2006: 249-253.
|
| [25] |
Chen C, Vaidyanathan P P. MIMO radar space-time adaptive processing using prolate spheroidal wave functions[J]. IEEE Trans, Signal Processing, 2008, 56(2): 623-635. DOI:10.1109/TSP.2007.907917 |
| [26] |
Abramovich Y I, Frazer G J, Johnson B A. Principles of mode-selective MIMO OTHR[J]. IEEE Trans on Aerospace and Electronic Systems, 2013, 49(3): 1839-1868. DOI:10.1109/TAES.2013.6558024 |
| [27] |
Xie W C, Zhang X C, Wang Y L, et al. Estimation of clutter degrees of freedom for airborne multiple-input multiple-output-phased array radar[J]. IET Radar, Sonar & Navigation, 2013, 7(6): 652-657. |
| [28] |
Gu F F, Chi L, Zhang Q, et al. Single snapshot imaging method in multiple-input multiple-output radar with sparse antenna array[J]. IET Radar Sonar & Navigation, 2013, 7(5): 535-543. |
| [29] |
Yao B B, Wang W J, Yin Q Y. DOD and DOA estimation in bistatic non-uniform multiple-input multiple-output radar systems[J]. IEEE Communications Letters, 2012, 16(11): 1796-1799. DOI:10.1109/LCOMM.2012.091212.121605 |
| [30] |
Tang B, Tang J, Zhang Y, et al. Maximum likelihood estimation of DOD and DOA for bistatic MIMO radar[J]. Signal Processing, 2013, 93(5): 1349-1357. DOI:10.1016/j.sigpro.2012.11.011 |
| [31] |
Daum F, Huang J. MIMO radar snake oil or good idea[J]. IEEE Aerospace and Electronic Systems Magazine, 2009, 5: 8-12. |
| [32] |
Colone F. Antenna sidelobes level control in transmit subaperturing MIMO radar[J]. IEEE Trans on Aerospace and Electronic Systems, 2017, 53: 1321-1340. DOI:10.1109/TAES.2017.2670898 |
| [33] |
Haghnegahdar M. SINR enhancement in colocated MIMO radar using transmit covariance matrix optimization[J]. IEEE Signal Processing Letters, 2017, 24(3): 339-343. DOI:10.1109/LSP.2017.2663406 |
| [34] |
保铮, 张庆文. 一种新型的米波雷达-综合脉冲与孔径雷达[J]. 现代雷达, 1995, 17(1): 1-13. Bao Zheng, Zhang Qingwen. A new style metric wave radar-synthetic impulse and aperture radar[J]. Modern Radar, 1995, 17(1): 1-13. |
| [35] |
Guerci J R. Cognitive radar:The knowledge-aidely fully adaptive approach[M]. USA: Artech House, Inc., 2010.
|
 2018, Vol. 33
2018, Vol. 33

