自从1948年香农创建信息论以来[1],通信领域已经取得了丰硕成果,这些成果为通信技术的飞速发展奠定了坚实的基础。香农信道容量理论是信道编码的基本理论基础,而信息速率失真函数理论是信源编码的理论基础。在20世纪90年代,Telatar研究了MIMO系统的信道容量[2],证明了通过增加接收天线数量,系统容量将会成倍数的增加。
雷达和声纳,已被广泛应用于军事、工业和医疗领域,都是使用回波信号来检测目标的电子系统,通过发射脉冲和回波信号的时间差,即可得到发射点与目标的精确距离。迄今为止,在雷达检测中,Woodward等人首次研究了雷达检测中的位置信息问题[3-4],在高信噪比条件下,得到了位置信息与信噪比的关系。遗憾的是,此后60多年来国际上一直没有该方向的研究进展。信息论方法还被用于雷达关于目标识别和分类的雷达波形设计[5]问题,2007年在文献[6]中进行了讨论,在相同总功率的约束条件下,对于描述最佳波形设计基本组成的矩阵,由信息的最大化和MMSE准则的最小化得到了相同的解。已经证明,相对熵可以用于测量雷达系统中的检测性能,相对熵越大,获得的性能越好。波形设计被认为是一种在白噪声条件下的统计MIMO雷达系统[7],文献[8]中考虑在有色噪声背景下设计MIMO雷达波形。
本文运用香农信息论的思想和方法,研究在单目标情形下雷达目标探测时的信息理论。假设目标位置的先验分布为均匀分布,目标的散射系数分为常数和服从瑞利分布两种模型,推导出位置信息和幅相信息的闭合表达式。在高信噪比下,目标的位置信息与时间带宽积和信噪比的对数成线性关系,通过仿真进一步说明理论结果的正确性,给出了中低信噪比下雷达探测目标获得的信息量。
符号说明:大写字母表示随机变量,相应的小写字母表示变量的取值。
1 雷达目标探测系统模型雷达探测的目的是从回波信号中获取目标的距离和幅相信息。通常,距离分辨的精度由均方误差表示,目标的大小由信号的幅相来衡量。令s(t)表示实际的基带信号,当载波频率和初始相位分别为fc,φ0时,发送信号可以表示为s(t)ej(2πfct+φ0)。假设参考点是观测区间的中心,其坐标为0,观测区间为
| $ z\left( t \right) = \alpha s\left( {t - \tau } \right){{\rm{e}}^{{\rm{j}}\left( { - 2{\rm{ \mathsf{ π} }}{f_{\rm{c}}}\tau + {\varphi _0}} \right)}} + w\left( t \right) = ys\left( {t - \tau } \right) + w\left( t \right) $ | (1) |
式中:τ=2d/v表示目标时延,y=αejφ,φ=-2πfcτ+φ0,w(t)为带宽B/2的复高斯噪声。雷达目标探测就是得到幅相参数y和位置参数τ的过程。在本文中,y被建模为复高斯变量,τ被建模为在检测范围内服从均匀分布的随机变量。
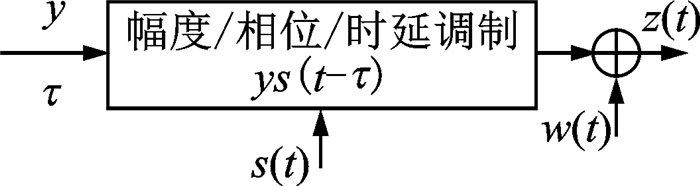
雷达探测系统的等效通信模型如图 1所示。
|
图 1 雷达探测系统的等效通信模型 Fig. 1 Equivalent communication model of radar detection system |
考虑以下低通信号
| $ s\left( t \right) = \sin c\left( {Bt} \right) = \frac{{\sin \left( {{\rm{ \mathsf{ π} }}Bt} \right)}}{{{\rm{ \mathsf{ π} }}Bt}}\;\;\;\; - \frac{{{T_s}}}{2} \le t \le \frac{{{T_s}}}{2} $ | (2) |
式中:Ts表示信号s(t)的持续时间,通常Ts≪T,即信号能量几乎全部在观测区间内,s(t)的频谱为
| $ S\left( f \right) = \left\{ \begin{array}{l} \frac{1}{B}\;\;\;\;\left| f \right| \le - \frac{B}{2}\\ 0\;\;\;\;\;其他 \end{array} \right. $ | (3) |
均方根带宽β2为
| $ {\beta ^2} = \frac{{{{\left( {2{\rm{ \mathsf{ π} }}} \right)}^2}\int_{ - \frac{B}{2}}^{\frac{B}{2}} {{f^2}{{\left| {S\left( f \right)} \right|}^2}{\rm{d}}f} }}{{\int_{ - \frac{B}{2}}^{\frac{B}{2}} {{{\left| {S\left( f \right)} \right|}^2}{\rm{d}}f} }} = \frac{{{{\rm{ \mathsf{ π} }}^2}}}{3}{B^2} $ | (4) |
实际的雷达系统通常采用线性调频信号、多载波信号和编码信号等。本文与香农信息论的方法类似,采用理想低通信号来推导理论结果。
s(t)的带宽是B/2,根据Shannon-Nyquist采样定理,以速率B对信号z(t)进行采样,z(t)的采样序列为
| $ z\left( n \right) \buildrel \Delta \over = z\left( {\frac{n}{B}} \right) = ys\left( {\frac{{\left( {n - \tau B} \right)}}{B}} \right) + w\left( {\frac{n}{B}} \right)\;\;\;\;n = - \frac{N}{2}, \cdots ,\frac{N}{2} - 1 $ | (5) |
式中N=TB,称为时间带宽积(Time bandwidth product, TBP)。z(t)能够被序列z(n)的N个点重建,图 2表示接收机的连续波形和离散波形。

|
图 2 3种观测区间与信号波形 Fig. 2 Three observation intervals and signal waveforms |
图 2(a)表示观测距离区间,目标位于区间中点,图 2(b)表示观测时间区间与回波信号,图 2(c)表示归一化观测区间与离散回波信号,本文主要讨论在归一化观测区间探测信息的结果。
令X=Bτ,表示目标的归一化延迟,进而可以得到
| $ z\left( n \right) = ys\left( {n - X} \right) + w\left( n \right) $ | (6) |
定义从目标反射的有用信号平均能量和复高斯噪声实部功率的比值为信噪比,即
| $ {\rho ^2} = \frac{{E\left( {\sum\limits_{n = - \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {ys\left( {n - X} \right)} \right|}^2}} } \right)}}{{\frac{{{N_0}}}{2}}} = \frac{{2E\left( {{\alpha ^2}} \right)}}{{{N_0}}} $ |
式中N0表示噪声的功率谱密度。
将式(6)写成矢量形式
| $ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{U}}\left( X \right)Y + \mathit{\boldsymbol{W}} $ | (7) |
式中:Z=[z(-N/2), …, z(N/2-1)]T表示探测统计量,W=[w(-N/2), …, w(N/2-1)T表示噪声矢量,而U(X)=[sinc(-N/2-X),…,sinc(N/2-1)-X)]T表示经过延迟的信号。雷达检测的目的是从矢量Z中估计出位置参数X和幅相相位参数Y,令I(Z; X, Y)表示从采样序列z中获得的关于X和Y的信息量。根据互信息的性质,有
| $ I\left( {\mathit{\boldsymbol{Z}};X,Y} \right) = I\left( {\mathit{\boldsymbol{Z}},X} \right) = I\left( {\mathit{\boldsymbol{Z}},Y\left| X \right.} \right) $ | (8) |
式中:I(Z, X)表示目标的位置信息,I(Z, Y|X)表示在X已知条件下目标的幅相相位信息。目标的幅相相位信息依赖于位置信息。因此,雷达目标探测可以分为两个步骤,首先确定目标的位置信息I(Z, X),然后在已知位置条件下确定目标的幅相相位信息I(Z, Y|X)。
2 目标的位置信息 2.1 目标的概率模型假设目标在检测范围内独立地均匀分布,则X的先验概率密度为p(x)=1/N。当载波频率非常高时,时延较小的变化将导致相位的巨大变化。因此,将φ视为在区间[0, 2π]上服从均匀分布的随机变量,则Φ的先验概率密度为p(φ)=1/2π。
对于目标的散射系数,将分别考虑两种不同的情况。(1)当散射系数为常数时,幅相相位信息就退化为相位信息;(2)将散射系数建模为瑞利分布的随机变量,这种情况下,Y被建模为复高斯向量。接下来,分别讨论散射系数不同情况下的位置信息和幅相相位信息。
w为低通带限白噪声,它的自相关函数为[9]
| $ R\left( {\tau '} \right) = \frac{{{n_0}B\sin {\rm{ \mathsf{ π} }}B\tau '}}{{2{\rm{ \mathsf{ π} }}B\tau '}} $ | (9) |
式中:n0=N0/B,n0为噪声的单边功率谱密度。由式(9)可知,在1/B的整数间隔上得到的随机变量互不相关,因w是高斯的,故w的采样值之间相互独立。W是均值为0,方差为N0的复高斯随机矢量,它的元素独立同分布,所以N维噪声矢量的概率密度函数为
| $ p\left( \mathit{\boldsymbol{w}} \right) = {\left( {\frac{1}{{{\rm{ \mathsf{ π} }}{N_0}}}} \right)^N}\exp \left\{ { - \frac{1}{{{N_0}}}\sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {w\left( n \right)} \right|}^2}} } \right\} $ | (10) |
式中
考虑归一化时延为x0时的单目标检测模型为
| $ z\left( n \right) = \alpha {{\rm{e}}^{{\rm{j}}{\varphi _0}}}s\left( {n - {x_0}} \right) + w\left( n \right)\;\;\;\;\;n = - \frac{N}{2}, \cdots ,\frac{N}{2} - 1 $ | (11) |
假设W为复高斯矢量,在给定X和Φ的条件下,Z的多维概率密度函数为
| $ p\left( {\mathit{\boldsymbol{z}}\left| {x,\varphi } \right.} \right) = {\left( {\frac{1}{{{\rm{ \mathsf{ π} }}{N_0}}}} \right)^N}\exp \left( { - \frac{1}{{{N_0}}}\sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {z\left( n \right) - \alpha {{\rm{e}}^{{\rm{j}}\varphi }}\sin c\left( {n - x} \right)} \right|}^2}} } \right) $ | (12) |
给定条件Φ,Z和X的联合概率密度为
| $ p\left( {\mathit{\boldsymbol{z}}\left| {x,\varphi } \right.} \right) = \frac{1}{N}{\left( {\frac{1}{{{\rm{ \mathsf{ π} }}{N_0}}}} \right)^N}\exp \left( { - \frac{1}{{{N_0}}}\left( {\sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {z\left( n \right)} \right|}^2} + {\alpha ^2}} } \right)} \right) \\ \cdot \exp \left( {\frac{{2\alpha }}{{{N_0}}}R\left( {{{\rm{e}}^{ - {\rm{j}}\varphi }}\sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {z\left( n \right)\sin c\left( {n - x} \right)} } \right)} \right) $ | (13) |
z和x的联合概率密度函数为
| $ p\left( {x\left| \mathit{\boldsymbol{z}} \right.} \right) = \frac{{\int_0^{2{\rm{ \mathsf{ π} }}} {\exp \left( {\frac{{2\alpha }}{{{N_0}}}{\mathop{\rm Re}\nolimits} \left( {{{\rm{e}}^{ - {\rm{j}}\varphi }}\sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {z\left( n \right)\sin c\left( {n - x} \right)} } \right)} \right){\rm{d}}\varphi } }}{{\int_{ - \frac{N}{2}}^{\frac{N}{2} - 1} {\int_0^{2{\rm{ \mathsf{ π} }}} {\exp \left( {\frac{{2\alpha }}{{{N_0}}}{\mathop{\rm Re}\nolimits} \left( {{{\rm{e}}^{ - {\rm{j}}\varphi }}\sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {z\left( n \right)\sin c\left( {n - x} \right)} } \right)} \right){\rm{d}}\varphi {\rm{d}}x} } }} $ | (14) |
式中Re表示取实部。
令
| $ A\left( {x,\mathit{\boldsymbol{w}}} \right) = \sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {w\left( n \right)\sin c\left( {n - x} \right)} $ |
代入式(14)可以得到
| $ p\left( {x\left| \mathit{\boldsymbol{w}} \right.} \right) = \frac{{{\mathit{\boldsymbol{I}}_0}\left( {{\rho ^2}\left| {\sin c\left( {x - {x_0}} \right) + \frac{1}{\alpha }A\left( {x,\mathit{\boldsymbol{w}}} \right)} \right|} \right)}}{{\int_{ - \frac{N}{2}}^{\frac{N}{2} - 1} {{I_0}\left( {{\rho ^2}\left| {\sin c\left( {x - {x_0}} \right) + \frac{1}{\alpha }A\left( {x,\mathit{\boldsymbol{w}}} \right)} \right|} \right){\rm{d}}x} }} $ | (15) |
式中I0(·)表示第一类零阶修正贝塞尔函数。
目标的位置X在检测范围内服从均匀分布,因此可以得到X的信息熵为H(X)=logN,进而可以计算出单目标检测时的位置信息
| $ I\left( {\mathit{\boldsymbol{Z}},X} \right) = H\left( X \right) - H\left( {X\left| \mathit{\boldsymbol{Z}} \right.} \right) = H\left( X \right) - {E_w}\left[ {H\left( {X\left| \mathit{\boldsymbol{w}} \right.} \right)} \right] = \\ \log N - \int_w {H\left( {X\left| \mathit{\boldsymbol{w}} \right.} \right)p\left( \mathit{\boldsymbol{w}} \right){\rm{d}}\mathit{\boldsymbol{w}}} $ | (16) |
式中
当散射系数服从瑞利分布时,此时目标的幅相变化很缓慢,因此它的概率分布为
| $ p\left( \alpha \right) = \frac{\alpha }{{\sigma _\alpha ^2}}{{\rm{e}}^{ - \frac{{{\alpha ^2}}}{{2\sigma _\alpha ^2}}}} $ | (17) |
式中α≥0且α的均值是2σα2。类似地,在给定幅相和相位的条件下,Z和X的联合概率密度为
| $ p\left( {\mathit{\boldsymbol{z}},x\left| {\alpha ,\varphi } \right.} \right) = \frac{1}{N}{\left( {\frac{1}{{{\rm{ \mathsf{ π} }}{N_0}}}} \right)^N}\exp \left( { - \frac{1}{{{N_0}}}\left( {\sum\limits_{n = - \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {z\left( n \right)} \right|}^2} + {\alpha ^2}} } \right)} \right)\\ \cdot \exp \left( {\frac{{2\alpha }}{{{N_0}}}{\mathop{\rm Re}\nolimits} \left( {{{\rm{e}}^{ - {\rm{j}}\varphi }}\sum\limits_{n =- \frac{N}{2}}^{\frac{N}{2} - 1} {z\left( n \right)\sin c\left( {n - x} \right)} } \right)} \right) $ | (18) |
因此
| $ \begin{array}{*{20}{c}} {p\left( {\mathit{\boldsymbol{w}},x} \right) = \int_0^\infty {\int_0^{2{\rm{ \mathsf{ π} }}} {p\left( {\mathit{\boldsymbol{z}},x\left| {\alpha ,\varphi } \right.} \right)p\left( \alpha \right)p\left( \varphi \right){\rm{d}}\alpha {\rm{d}}\varphi } } \propto }\\ {\int_0^\infty {\exp \left( { - \frac{{{\alpha ^2}}}{{{N_0}}}} \right){I_0}\left( {\frac{{2{\alpha ^2}}}{{{N_0}}}\left| {\sin c\left( {x - {x_0}} \right) + \frac{1}{\alpha }A\left( {x,\mathit{\boldsymbol{w}}} \right)} \right|} \right)p\left( \alpha \right){\rm{d}}\alpha } } \end{array} $ | (19) |
进一步可由
| $ p\left( {x\left| \mathit{\boldsymbol{w}} \right.} \right) = \frac{{p\left( {\mathit{\boldsymbol{w}},x} \right)}}{{\int_{ - \frac{N}{2}}^{\frac{N}{2} - 1} {p\left( {\mathit{\boldsymbol{w}},x} \right){\rm{d}}x} }} $ | (20) |
代入式(16)可得到散射系数为瑞利分布时的位置信息(注:式(19)中使用∝是因为在式(20)中分子分母存在相同的与积分无关的常数项)。
2.4 位置信息与克拉美罗界的关系克拉美罗界(Cramér-Rao Bound,CRB)指的是随机参量x的估计值所能达到的最小均方误差。高信噪比时,归一化时延x的CRB为Var(x)≥[(2E(α2)/N0)β2]-1[10] (归一化时延情况下β2=π2/3),令
| $ \sigma _{{\rm{CRB}}}^2 = \frac{{2E\left( {{\alpha ^2}} \right)}}{{{N_0}}}{\beta ^2} = {\rho ^2}{\beta ^2} $ | (21) |
假设目标位置的估计值服从高斯分布,微分熵为
| $ I\left( {\mathit{\boldsymbol{Z}},X} \right) \le \log N - \frac{1}{2}\log 2{\rm{ \mathsf{ π} e}}\sigma _{{\rm{CRB}}}^2 = \log \frac{{T\beta \rho }}{{\sqrt {2{\rm{ \mathsf{ π} }}e} }} $ | (22) |
即为高信噪比下目标位置信息的CRB。
3 目标的幅相相位信息 3.1 目标散射系数为常数的幅相信息当散射系数为常数时,幅相相位信息I(Z, Y|X)等同于相位信息I(Z, Φ|X)。首先,在给定条件X和Y的情况下,Z的多维概率密度函数为
| $ p\left( {\mathit{\boldsymbol{z}}\left| {x,y} \right.} \right) = {\left( {\frac{1}{{{\rm{ \mathsf{ π} }}{N_0}}}} \right)^N}\exp \left( { - \frac{1}{{{N_0}}}\sum\limits_{n = - \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {z\left( n \right) - y\sin c\left( {n - x} \right)} \right|}^2}} } \right) $ | (23) |
将y=αejφ代入得到
| $ p\left( {\mathit{\boldsymbol{z}}\left| {x,\varphi } \right.} \right) = {\left( {\frac{1}{{{\rm{ \mathsf{ π} }}{N_0}}}} \right)^N}\exp \left( { - \frac{1}{{{N_0}}}\sum\limits_{n = - \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {z\left( n \right) - \alpha {{\rm{e}}^{{\rm{j}}\varphi }}\sin c\left( {n - x} \right)} \right|}^2}} } \right) $ | (24) |
可以推导出
| $ p\left( {\varphi \left| {\mathit{\boldsymbol{z}},x} \right.} \right) = \frac{{\exp \left( { - \frac{1}{{{N_0}}}\sum\limits_{n = - \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {z\left( n \right) - \alpha {{\rm{e}}^{{\rm{j}}\varphi }}\sin c\left( {n - x} \right)} \right|}^2}} } \right)}}{{\int_0^{2{\rm{ \mathsf{ π} }}} {\left( { - \frac{1}{{{N_0}}}\sum\limits_{n = - \frac{N}{2}}^{\frac{N}{2} - 1} {{{\left| {z\left( n \right) - \alpha {{\rm{e}}^{{\rm{j}}\varphi }}\sin c\left( {n - x} \right)} \right|}^2}} } \right){\rm{d}}\varphi } }} $ | (25) |
采用式(25),进一步可以得到
| $ p\left( {\varphi \left| {\mathit{\boldsymbol{w}},x} \right.} \right) = \frac{{\exp \left( {\frac{{2\alpha }}{{{N_0}}}{\mathop{\rm Re}\nolimits} \left( {{{\rm{e}}^{ - {\rm{j}}\varphi }}\left( {\alpha {{\rm{e}}^{{\rm{j}}{\varphi _0}}}\sin c\left( {x - {x_0}} \right) + A\left( {x,\mathit{\boldsymbol{w}}} \right)} \right)} \right)} \right)}}{{2{\rm{ \mathsf{ π} }}{I_0}\left( {{\rho ^2}\left| {\sin c\left( {x - {x_0}} \right) + \frac{1}{\alpha }A\left( {x,\mathit{\boldsymbol{w}}} \right)} \right|} \right)}} $ | (26) |
根据互信息的性质,相位信息由式(27)给出
| $ I\left( {\mathit{\boldsymbol{Z}},\mathit{\Phi }\left| X \right.} \right) = H\left( {\mathit{\Phi }\left| X \right.} \right) - H\left( {\mathit{\Phi }\left| {\mathit{\boldsymbol{Z}},X} \right.} \right) = \log \left( {2{\rm{ \mathsf{ π} }}} \right) - {E_{x,w}}\left[ {H\left( {\varphi \left| {\mathit{\boldsymbol{w}},x} \right.} \right)} \right] $ | (27) |
式中
在估计了目标的位置后,U(X)矩阵是一个常数矩阵,既然Y和W都是独立的高斯分布,由此可知Z也是一个高斯矢量。
首先有
| $ \begin{array}{*{20}{c}} {E\left[ {\mathit{\boldsymbol{Z}}{\mathit{\boldsymbol{Z}}^{\rm{H}}}} \right] = E\left[ {\left( {\mathit{\boldsymbol{U}}\left( X \right)Y + \mathit{\boldsymbol{W}}} \right){{\left( {\mathit{\boldsymbol{U}}\left( X \right)Y + \mathit{\boldsymbol{W}}} \right)}^{\rm{H}}}} \right] = }\\ {\mathit{\boldsymbol{U}}\left( X \right)E\left[ {Y{Y^{\rm{H}}}} \right]{\mathit{\boldsymbol{U}}^{\rm{H}}}\left( X \right) + E\left[ {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}^{\rm{H}}}} \right] = E\left[ {{\alpha ^2}} \right]\mathit{\boldsymbol{U}}\left( X \right){\mathit{\boldsymbol{U}}^{\rm{H}}}\left( X \right) + \frac{{{N_0}}}{2}\mathit{\boldsymbol{I}}} \end{array} $ | (28) |
可以得出
| $ H\left( {\mathit{\boldsymbol{Z}}\left| {X = x} \right.} \right) = \log \left| {E\left[ {{\alpha ^2}} \right]\mathit{\boldsymbol{U}}\left( x \right){\mathit{\boldsymbol{U}}^{\rm{H}}}\left( x \right) + \frac{{{N_0}}}{2}\mathit{\boldsymbol{I}}} \right|\mathit{\boldsymbol{ + }}N\log \left( {2{\rm{ \mathsf{ π} e}}} \right) $ | (29) |
而且
| $ H\left( {\mathit{\boldsymbol{Z}}\left| {X = x,Y} \right.} \right) = H\left( \mathit{\boldsymbol{W}} \right) = \log \left| {\frac{{{N_0}}}{2}\mathit{\boldsymbol{I}}} \right| + N\log \left( {2{\rm{ \mathsf{ π} e}}} \right) $ | (30) |
因此,在已知条件X=x时,幅相相位信息为
| $ {I\left( {\mathit{\boldsymbol{Z}},Y\left| {X = x} \right.} \right) = H\left( {\mathit{\boldsymbol{Z}}\left| {X = x} \right.} \right) - H\left( {\mathit{\boldsymbol{Z}}\left| {X = x} \right.,Y} \right) =\\ \log \left| {E\left[ {{\alpha ^2}} \right]\mathit{\boldsymbol{U}}\left( x \right){\mathit{\boldsymbol{U}}^{\rm{H}}}\left( x \right) + \frac{{{N_0}}}{2}\mathit{\boldsymbol{I}}} \right| - \log \left| {\frac{{{N_0}}}{2}\mathit{\boldsymbol{I}}} \right| = }\\ {\log \left| {\mathit{\boldsymbol{I}} + \frac{{2E\left[ {{\alpha ^2}} \right]}}{{{N_0}}}\mathit{\boldsymbol{U}}\left( x \right){\mathit{\boldsymbol{U}}^{\rm{H}}}\left( x \right)} \right| = \\\log \left( {1 + {\rho ^2}{\mathit{\boldsymbol{U}}^{\rm{H}}}\left( x \right)\mathit{\boldsymbol{U}}\left( x \right)} \right)} $ | (31) |
此外,对于
| $ {\mathit{\boldsymbol{U}}^{\rm{H}}}\left( x \right)\mathit{\boldsymbol{U}}\left( x \right) = \sum\limits_{n = - \frac{N}{2}}^{\frac{N}{2} - 1} {\sin {c^2}\left( {n - x} \right) \approx 1} $ |
将UH(x)U(x)的结果代入式(31),可以得到
| $ I\left( {\mathit{\boldsymbol{Z}},Y\left| {X = x} \right.} \right) = \log \left( {1 + {\rho ^2}} \right) $ |
这意味着I(Z, Y|X=x)与目标估计的归一化时延无关,即目标的幅相信息与位置信息无关。因此,当目标散射系数服从瑞利分布,相位服从均匀分布时,Y可以视为一个复高斯随机变量。此时雷达系统中单目标检测的幅相相位信息为
| $ I\left( {\mathit{\boldsymbol{Z}},Y\left| X \right.} \right) = \log \left( {1 + {\rho ^2}} \right) $ | (32) |
本文从两个方面来进行仿真分析:(1)位置信息与信噪比以及位置信息与克拉美罗界的关系;(2)散射系数为常数和服从瑞利分布两种情形下,幅相信息与信噪比的关系。
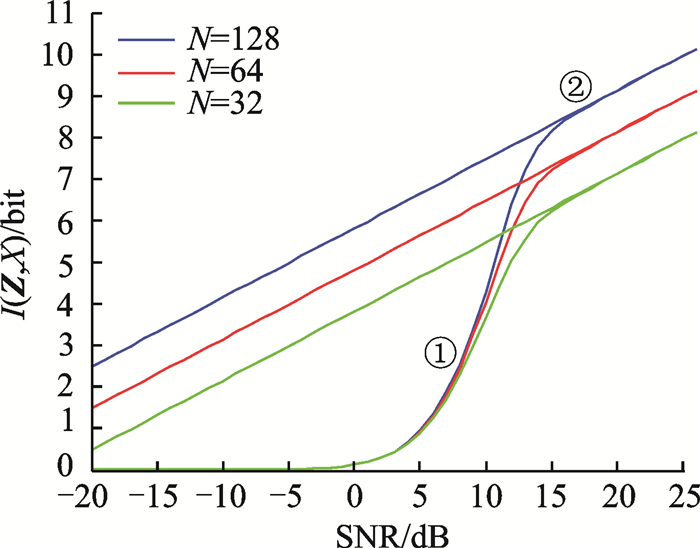
4.1 不同时间带宽积下位置信息与信噪比的关系参数N分别选择128, 64, 32,将目标位置设在x0=0处,CAWGN信道,散射系数α=1。可以看出,位置信息与时间带宽积的对数成线性关系,随信噪比的增大而增大,且N越大,获得的信息量越多, 这是因为不同N值对应的信息熵H(X)不同。图 3中的虚直线是高信噪比下的克拉美罗界近似值,即I(Z, X)≈
|
图 3 不同N下位置信息随信噪比的变化曲线 Fig. 3 Relationship between location information and SNR under different N |
目标探测过程中,当信噪比很小时,噪声干扰较大,无法发现目标,位置信息很小。随着信噪比的增加,位置信息的变化划分为两个重要的阶段:(1)目标捕获阶段:超过0 dB后,位置信息随SNR以较大的斜率增加,每增加1 bit,意味着目标的位置区域减小一半。当信息量达到logTB时,目标区域缩小至观测区间的1/TB,即系统分辨率达到1/B。(2)目标跟踪阶段:在大SNR区域,位置信息与时间带宽积的对数成线性关系,且随信息量增加,目标范围继续缩小,从而突破1/B的限制。
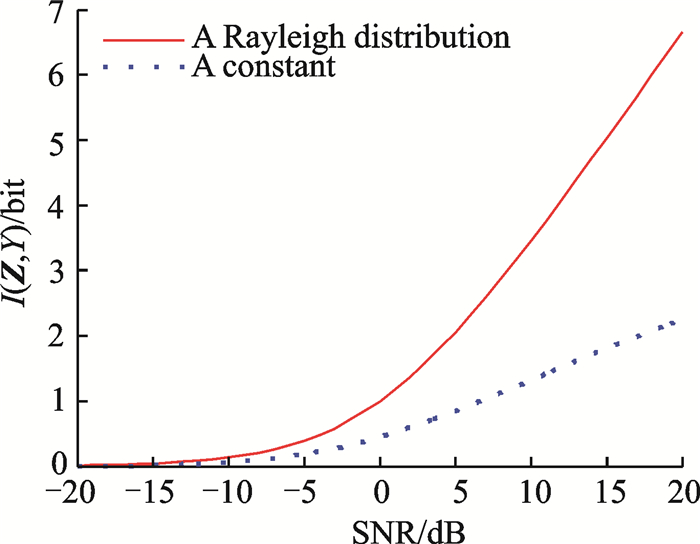
4.2 幅相信息与信噪比的关系散射系数α为常数和服从瑞利分布两种情形下,对应的幅相信息仿真曲线如图 4所示。可以看出幅相信息与信噪比成正比关系,随着信噪比的升高而升高。这样,位置信息I(Z, X)和幅相信息I(Z, Y|X)共同构成了雷达探测的信息I(Z; X, Y)。
|
图 4 幅相信息和信噪比的关系 Fig. 4 Relationship between amplitude-phase information and SNR |
5 结束语
本文将信息论的方法应用到雷达目标检测系统中,在单目标检测时推导了位置信息和幅相相位信息的闭合表达式,理论分析与数值结果表明雷达目标探测的两个重要阶段,即目标捕获阶段和目标跟踪阶段。在目标的跟踪阶段,由于克拉美罗界是最大似然算法的上界,因此本文得出的理论结果对实际系统的设计具有重要指导意义。在下一步研究计划中,多目标时的探测信息、如何设计雷达系统以达到或逼近本文给出的理论界限等问题都是值得进一步深入研究的重点。
| [1] |
Shannon C E. A mathematical theory of communication[J]. Bell Systeim Tech, 1948, 27(3): 379-423. DOI:10.1002/bltj.1948.27.issue-3 |
| [2] |
Telatar E. Capacity of multi-antenna Gaussian channels[J]. Eur Trans Telecommun, 1999, 10(6): 585-595. DOI:10.1002/ett.4460100604 |
| [3] |
Woodward P M. Theory of radar information[J]. Trans IRE Prof Gr Inf Theory, 1953, 1(1): 108-113. DOI:10.1109/TIT.1953.1188560 |
| [4] |
Woodward P M, Davies I L. A theory of radar information[J]. Dublin Philos Mag J Sci, 1950, 41(321): 1001-1017. DOI:10.1080/14786445008561035 |
| [5] |
WoodwardP M. Information theory and the design of radar receivers[J]. Proc IRE, 1951, 39(12): 1521-1524. DOI:10.1109/JRPROC.1951.273638 |
| [6] |
Yang Y, Blum R S. MIMO radar waveform design based on mutual information and minimum mean-square error estimation[J]. IEEE Trans Aerosp Electron Syst, 2007, 43(1): 330-343. DOI:10.1109/TAES.2007.357137 |
| [7] |
Kay S. Waveform design for multistatic radar detection[J]. IEEE Trans Aerosp Electron Syst, 2009, 45(3): 1153-1166. DOI:10.1109/TAES.2009.5259190 |
| [8] |
Tang Bo, Tang Jun, Peng Yingning. MIMO radar waveform design in colored noise based on information theory[J]. IEEE Trans Signal Process, 2010, 58(9): 4684-4697. DOI:10.1109/TSP.2010.2050885 |
| [9] |
樊昌信, 曹丽娜. 通信原理[M]. 6版. 北京: 国防工业出版社, 2010: 58-58.
|
| [10] |
Mcdonough R N, Whalen A D. Detection of signals in noise[M]. [S. l. ]: Academic Press, 1971: 411-411.
|
 2018, Vol. 33
2018, Vol. 33

