波达方向(Direction-of-arrival,DOA)估计是阵列信号处理的重要应用领域之一[1-2]。近年来,基于电磁矢量传感器阵列的信号DOA估计方法日益受到关注[3-4]。采用电磁矢量传感器阵列可以充分利用信号源极化信息、提高DOA估计精度,因而很多基于不同类型电磁矢量传感器阵列的信号DOA估计方法被相继提出。`文献[5, 6]分别提出了矢量叉积和单电磁矢量传感器源信号旋转不变信号参数估计(Estimation of signal parameters via rotational invariance techniques,ESPRIT)方法。采用交叉偶极子阵列,文献[7]提出了一种基于多重信号分类(Multiple signal classification,MUSIC)方法[8]的信号DOA估计方法,文献[9]则提出了一种基于ESPRIT的方法。然而这两种方法均为子空间类方法,无法处理相干源信号。
近年来压缩感知理论[10-12]迅速兴起,信号稀疏表示与重构(Sparse signal reconstruction,SSR)方法被用于解决信号DOA估计等一系列问题[13-17]。基于该理论框架的技术主要根据阵列协方差矩阵的结构特点来利用空域信息。具有代表性的SSR方法包括递归加权最小范数方法[18]、基于l1-范数惩罚的方法[19-20]及基于l2-范数惩罚的方法[21]。然而以上方法均针对基于标量阵列的窄带信号DOA估计。
文献[22]提出了一种基于同点正交磁环偶极子矢量天线(Co-centered orthogonal loop and dipole,COLD)阵列的稀疏表示窄带信号DOA估计方法,但没有利用COLD子阵列稀疏矢量的稀疏共性。对于宽带信号情形,已有的l1-范数奇异值分解(l1-norm singular value decomposition,l1-SVD)[19]方法首先进行频域分解至窄带后再进行DOA估计,最终的DOA估计结果是各个子窄带结果的平均值,同样没有充分利用各子窄带之间的联合稀疏性。
针对以上问题,本文提出一种基于COLD矢量天线均匀线阵的联合稀疏重构信号DOA估计方法。利用COLD阵列的特点构造极化-空间域协方差矩阵,并对其第一列进行稀疏表示。由于COLD天线由磁环与偶极子组成,稀疏矢量可由磁环构成的阵列与偶极子构成的阵列分别恢复。为了利用两个子阵列稀疏矢量的共性,采用l2-范数构造待恢复的联合稀疏矢量,进而基于凸优化(l1-范数)进行稀疏重构实现信号DOA估计。
1 COLD阵列信号模型考虑M个相互独立的窄带完全极化信号入射到如图 1所示的COLD矢量天线均匀线阵,其中矢量阵元数为L(L>M),矢量阵元间距为d(d≤c/2f),其中c为信号波传播速度,f为信号中心频率。

|
图 1 均匀COLD线阵 Fig. 1 A uniform linear COLD array |
注意到COLD阵列可看作由两个子阵构成,其中一个为偶极子阵,另一个为磁环阵。记偶极子阵的阵列输出为xD(t),磁环阵的阵列输出为xL(t),则COLD阵的输出矢量可表示为
| $ \mathit{\boldsymbol{x}}\left( t \right) = \left[ \begin{array}{l} {\mathit{\boldsymbol{x}}_D}\left( t \right)\\ {\mathit{\boldsymbol{x}}_L}\left( t \right) \end{array} \right] = \sum\limits_{m = 1}^M {{\mathit{\boldsymbol{a}}_m}{s_m}\left( t \right)} + \left[ \begin{array}{l} {\mathit{\boldsymbol{n}}_D}\left( t \right)\\ {\mathit{\boldsymbol{n}}_L}\left( t \right) \end{array} \right] $ | (1) |
式中:nD(t)和nL(t)分别为偶极子阵和磁环阵的空时-极化白加性高斯噪声矢量;am为第m个信号sm(t)的导向矢量
| $ {\mathit{\boldsymbol{a}}_m} = {\left[ {\mathit{\boldsymbol{a}}_{D,m}^{\rm{T}},\mathit{\boldsymbol{a}}_{L,m}^{\rm{T}}} \right]^{\rm{T}}} $ | (2) |
式中:(·)T表示转置,aD, m=-sinγmejηmas, m,aL, m=-cosγmas, m,并且as, m=[1, …, ej2πfldsinθm/c, …, ej2πf(L-1)dsinθm/c]T。而θm为第m个信号的DOA,γm和ηm则分别为第m个信号的极化辅助角和极化相位差。
为了便于处理,将式(1)所示阵列输出矢量重写为
| $ \mathit{\boldsymbol{x}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_D}}\\ {{\mathit{\boldsymbol{A}}_L}} \end{array}} \right]\mathit{\boldsymbol{s}}\left( t \right) + \left[ \begin{array}{l} {\mathit{\boldsymbol{n}}_D}\left( t \right)\\ {\mathit{\boldsymbol{n}}_L}\left( t \right) \end{array} \right] $ | (3) |
式中:s(t)=[s1(t), s2(t), …, sM(t)]T表示信号矢量;AD=[aD, 1, aD, 2, …, aD, M]和AL=[aL, 1, aL, 2, …, aL, M]分别为对应于偶极子阵和磁环阵的阵列流形矩阵。
2 基于联合稀疏重构的窄带信号DOA估计方法定义极化-空间域协方差矩阵为
| $ {\mathit{\boldsymbol{R}}_D} = E\left\{ {{\mathit{\boldsymbol{x}}_D}\left( t \right)\mathit{\boldsymbol{x}}_D^{\rm{H}}\left( t \right)} \right\} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{S}}_D}{\mathit{\boldsymbol{A}}^{\rm{H}}} + {\mathit{\boldsymbol{N}}_D} $ | (4) |
| $ {\mathit{\boldsymbol{R}}_L} = E\left\{ {{\mathit{\boldsymbol{x}}_L}\left( t \right)\mathit{\boldsymbol{x}}_L^{\rm{H}}\left( t \right)} \right\} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{S}}_L}{\mathit{\boldsymbol{A}}^{\rm{H}}} + {\mathit{\boldsymbol{N}}_L} $ | (5) |
式中(·)H表示共轭转置,且
| $ \mathit{\boldsymbol{A}} = \left[ {{\mathit{\boldsymbol{a}}_{s,1}},{\mathit{\boldsymbol{a}}_{s,2}}, \cdots ,{\mathit{\boldsymbol{a}}_{s,M}}} \right] $ |
| $ {\mathit{\boldsymbol{S}}_D} = {\rm{diag}}\left\{ {\sigma _1^2{{\sin }^2}\left( {{\gamma _1}} \right), \cdots ,\sigma _M^2{{\sin }^2}\left( {{\gamma _M}} \right)} \right\} $ |
| $ {\mathit{\boldsymbol{S}}_L} = {\rm{diag}}\left\{ {\sigma _1^2{{\cos }^2}\left( {{\gamma _1}} \right), \cdots ,\sigma _M^2{{\cos }^2}\left( {{\gamma _M}} \right)} \right\} $ |
| $ {\mathit{\boldsymbol{N}}_D} = {\mathit{\boldsymbol{N}}_L} = {\sigma ^2}\mathit{\boldsymbol{I}} $ |
其中:σm2表示第m个信号的功率;σ2表示噪声功率;I为单位矩阵。
利用式(4,5),进一步得到
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}_D} + {\mathit{\boldsymbol{R}}_L} = \mathit{\boldsymbol{A}}\left( {{\mathit{\boldsymbol{S}}_D} + {\mathit{\boldsymbol{S}}_L}} \right){\mathit{\boldsymbol{A}}^{\rm{H}}} + {\mathit{\boldsymbol{N}}_D} + {\mathit{\boldsymbol{N}}_L} = \sum\limits_{m = 1}^M {\sigma _m^2{\mathit{\boldsymbol{a}}_{s,m}}\mathit{\boldsymbol{a}}_{s,m}^{\rm{H}} + 2{\sigma ^2}\mathit{\boldsymbol{I}}} = }\\ {\left[ {\begin{array}{*{20}{c}} {\sum\limits_{m = 1}^M {\sigma _m^2 + 2{\sigma ^2}} }& \cdots &{\sum\limits_{m = 1}^M {\sigma _{\rm{m}}^2{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\left( {L - 1} \right)d\sin {\theta _m}/c}}} }\\ {\sum\limits_{m = 1}^M {\sigma _{\rm{m}}^2{{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}fd\sin {\theta _m}/c}}} }& \cdots &{\sum\limits_{m = 1}^M {\sigma _{\rm{m}}^2{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}f\left( {L - 2} \right)d\sin {\theta _m}/c}}} }\\ \vdots&\ddots&\vdots \\ {\sum\limits_{m = 1}^M {\sigma _{\rm{m}}^2{{\rm{e}}^{{\rm{j}}2{\rm{ \mathsf{ π} }}f\left( {L - 1} \right)d\sin {\theta _m}/c}}} }& \cdots &{\sum\limits_{m = 1}^M {\sigma _m^2 + 2{\sigma ^2}} } \end{array}} \right]} \end{array} $ | (6) |
定义矢量r0=[r21, r31, …, rL1]T,其中rij对应于协方差矩阵R的第(i, j)个元素,则r0可表示为
| $ {\mathit{\boldsymbol{r}}_0} = \mathit{\boldsymbol{Bp}} $ | (7) |
式中:B=A(2:L, :);p=[σ12, …, σm2, …, σM2]T。
为了利用信号的空域稀疏性来估计信号DOA,根据式(7),r0可进一步表示为
| $ {\mathit{\boldsymbol{r}}_0} = \overline {\mathit{\boldsymbol{Bp}}} $ | (8) |
式中,B=[bs, 1, bs, 2, …, bs, M′]为阵列流形矩阵扩展形成的过完备字典矩阵,由M′个包含所有可能存在的信号DOA对应的导向矢量构成,其中bs, m=as, m(2:L),p为稀疏矢量,且该矢量仅在有真实信号入射的位置值不为零,换句话说,p中非零元素的位置对应于信号DOA。再假设pD, pL为与具有相同结构的分别对应于偶极子阵和磁环阵的稀疏矢量,由于同一信号的DOA唯一且确定,于是pD, pL非零元素的位置应该相同,可以找到充分稀疏的唯一解。因此,本文提出一种联合pD, pL稀疏性来获得信号DOA的方法,称为联合稀疏重构窄带信号DOA估计方法(Narrowband joint sparse reconstruction, NJSR)。
为了便于描述,本文定义矢量
| $ \mathit{\boldsymbol{Z}} = {\left[ {{{\mathit{\boldsymbol{\bar p}}}_D},{{\mathit{\boldsymbol{\bar p}}}_L}} \right]^{\rm{T}}} = \left[ {{\mathit{\boldsymbol{z}}_1}, \cdots ,{\mathit{\boldsymbol{z}}_m}, \cdots ,{\mathit{\boldsymbol{z}}_{M'}}} \right] $ | (9) |
| $ \mathit{\boldsymbol{\bar z}} = {\left[ {{{\left\| {{\mathit{\boldsymbol{z}}_1}} \right\|}_2}, \cdots ,{{\left\| {{\mathit{\boldsymbol{z}}_m}} \right\|}_2}, \cdots ,{{\left\| {{\mathit{\boldsymbol{z}}_{M'}}} \right\|}_2}} \right]^{\rm{T}}} $ | (10) |
式中:zm(m=1, …, M′)表示Z的第m列;‖·‖2表示l2-范数。那么,信号DOA可通过求解下面的问题来获得
| $ \mathop {\min }\limits_{\tilde p} {\left\| {\mathit{\boldsymbol{\bar z}}} \right\|_1}{\rm{subject}}\;{\rm{to}}{\left\| {{\mathit{\boldsymbol{r}}_0} - {{\mathit{\boldsymbol{\bar B}}}_z}\mathit{\boldsymbol{\tilde p}}} \right\|_2} \le {\varepsilon _1} $ | (11) |
式中:Bz=[B, B];ε1是可允许的边界误差。ε1的选择决定了DOA的估计精度。本文使用CVX来求解式(11)获得信号DOA。
3 基于联合稀疏重构的宽带信号DOA估计方法与窄带信号相比,宽带信号有一段相对较宽的频带范围。然而,同一信号的波达方向并不会由于频率的不同而改变。基于这一特性,本文将所提窄带方法推广至宽带情形,提出了一种联合稀疏重构宽带信号DOA估计方法(Wideband joint sparse reconstruction, WJSR)。一方面,在宽带信号整个频率范围内联合利用DOA信息,本文将这种不同频率下的稀疏矢量所具有的稀疏共性称为稀疏集;另一方面,利用COLD阵列协方差矩阵特点构造用于稀疏恢复的联合稀疏矢量。
将宽带信号频带离散为Q个窄带频率集。本文仍需获得极化-空间域协方差矩阵R并定义矢量r0,方法同窄带情形。与窄带情形相比,宽带情形的r0包含了Q个窄带频率集的信息而非单一窄带频率集。
构造两个M′×Q矩阵PD和PL分别对应于偶极子阵和磁环阵
| $ {{\mathit{\boldsymbol{\bar P}}}_D} = \left[ {{{\mathit{\boldsymbol{\bar p}}}_{D,1}}, \cdots ,{{\mathit{\boldsymbol{\bar p}}}_{D,q}}, \cdots ,{{\mathit{\boldsymbol{\bar p}}}_{D,Q}}} \right] $ | (12) |
| $ {{\mathit{\boldsymbol{\bar P}}}_L} = \left[ {{{\mathit{\boldsymbol{\bar p}}}_{L,1}}, \cdots ,{{\mathit{\boldsymbol{\bar p}}}_{L,q}}, \cdots ,{{\mathit{\boldsymbol{\bar p}}}_{L,Q}}} \right] $ | (13) |
式中,pD, q和pL, q为对应于第q(q=1, …, Q)个窄带频率集的M′维稀疏矢量。构造如下虚拟阵列模型
| $ {\mathit{\boldsymbol{r}}_0} = {{\mathit{\boldsymbol{\tilde B}}}_z}\mathit{\boldsymbol{t}} $ | (14) |
式中
| $ {{\mathit{\boldsymbol{\tilde B}}}_z} = \left[ {{{\mathit{\boldsymbol{\tilde B}}}_1}, \cdots ,{{\mathit{\boldsymbol{\tilde B}}}_q}, \cdots ,{{\mathit{\boldsymbol{\tilde B}}}_Q},{{\mathit{\boldsymbol{\tilde B}}}_1}, \cdots ,{{\mathit{\boldsymbol{\tilde B}}}_q}, \cdots ,{{\mathit{\boldsymbol{\tilde B}}}_Q}} \right] $ |
| $ \mathit{\boldsymbol{t}} = {\rm{vec}}\left\{ {\left[ {{{\mathit{\boldsymbol{\bar P}}}_D},{{\mathit{\boldsymbol{\bar P}}}_L}} \right]} \right\} $ |
其中:Bq为对应于频率fq的与B具有相同构造的字典矩阵;t为2M′Q维稀疏矢量;vec{·}表示矩阵矢量化。
为了联合恢复pD和pL,本文再定义如下矩阵和矢量
| $ \mathit{\boldsymbol{\tilde Z}} = {\left[ {{{\mathit{\boldsymbol{\bar P}}}_D},{{\mathit{\boldsymbol{\bar P}}}_L}} \right]^{\rm{T}}} = \left[ {{{\mathit{\boldsymbol{\tilde z}}}_1}, \cdots ,{{\mathit{\boldsymbol{\tilde z}}}_m}, \cdots ,{{\mathit{\boldsymbol{\tilde z}}}_{M'}}} \right] $ |
| $ \mathit{\boldsymbol{\bar {\tilde z}}} = {\left[ {{{\left\| {{{\mathit{\boldsymbol{\tilde z}}}_1}} \right\|}_2}, \cdots ,{{\left\| {{{\mathit{\boldsymbol{\tilde z}}}_m}} \right\|}_2}, \cdots ,{{\left\| {{{\mathit{\boldsymbol{\tilde z}}}_{M'}}} \right\|}_2}} \right]^{\rm{T}}} $ |
其中
| $ \mathop {\min }\limits_t {\left\| {\mathit{\boldsymbol{\bar {\tilde z}}}} \right\|_1}{\rm{subject}}\;{\rm{to}}{\left\| {{\mathit{\boldsymbol{r}}_0} - {{\mathit{\boldsymbol{\bar B}}}_z}\mathit{\boldsymbol{t}}} \right\|_2} \le {\varepsilon _2} $ | (15) |
式中ε2为可允许的边界误差。
4 仿真实验与性能分析在本文仿真实验中,考虑一个6元线性均匀COLD阵列,阵元间距为半波长(若入射信号为宽带信号,则为信号最高频率所对应的半波长)。过完备字典DOA搜索网格范围为[-90°, 90°],网格步长为1°。可允许的误差边界ε1, ε2的最优值通过多次实验获得。
4.1 实验1:窄带入射信号情形下的信号DOA估计实验1基于以下两个场景:(1)两个等功率的远场窄带信号从θ1=35°,θ2=40°入射,对应的极化参数分别为(45°, 60°)和(30°, 60°),快拍数为200,信噪比(Signal-to-noise ratio,SNR)为20 dB,阈值ε1=0.000 8;(2)两个等功率的远场窄带信号从θ1=-35°,θ2=45°入射,对应的极化参数分别为(30°, 75°)和(20°, 60°),快拍数为100,SNR为5 dB,阈值ε1=0.000 8。在以下所有窄带入射信号情形的仿真中,本文将所提的NJSR方法与文献[22]中的TY方法进行性能比较。图 2为实验1条件下NJSR方法和TY方法的空间谱结果。

|
图 2 实验1条件下的空间谱 Fig. 2 Spatial spectrum versus DOAs of experiment 1 |
从图 2可以看出,本文提出的NJSR方法对两个不同间隔的信源具有较好的分辨能力,即使两个信号DOA邻近,NJSR也能得到精度较高的估计结果,而在同等条件下TY方法则无法准确分辨两个信号。此外,在低信噪比、短快拍条件下,NJSR方法同样显示出较好的分辨性能。
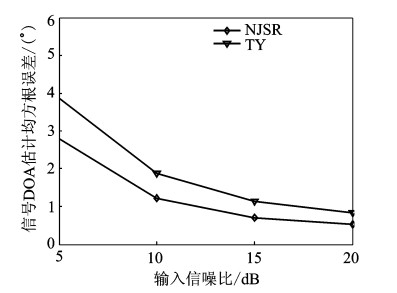
4.2 实验2:窄带入射信号情形下的估计精度两个等功率的远场窄带信号入射到阵列,方位角分别为θ1=35°和θ2=50°,对应的极化参数分别为(45°, 60°)和(30°, 60°)。快拍数为200,将其SNR在5~20 dB之间变化,变化间隔为5 dB,不同SNR下分别进行100次独立试验,对每个SNR下的100次独立试验结果求平均得到均方根误差(Root mean squared error,RMSE)随SNR的变化曲线,如图 3所示。RMSE定义为
|
图 3 RMSE随输入SNR变化曲线 Fig. 3 Curve of RMSE versus input SNR |
| $ {\rm{RMSE}} = \sqrt {\sum\limits_{j = 1}^J {\sum\limits_{m = 1}^M {{{\left( {{{\hat \theta }_{m,j}} - {{\hat \theta }_m}} \right)}^2}/MJ} } } $ | (16) |
式中
从图 3可以看出,估计精度随着SNR的增加而提高,本文所提的NJSR方法的性能明显优于TY方法。原因在于随着SNR的增加,信号功率逐渐变大,信号特性愈加显现,本文方法基于信号的稀疏特性,联合利用COLD阵列两个子阵的稀疏矢量找到充分稀疏的唯一解,稀疏信号重构更精确。
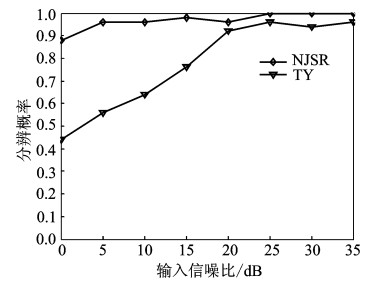
4.3 实验3:窄带入射信号情形下的分辨概率两个等功率的远场窄带信号DOA分别为θ1=35°和θ2=60°,将其SNR在0~35 dB之间变化,其余实验条件同实验2,实验结果为分辨概率(Resolution probability,RSPB)随SNR的变化曲线如图 4所示。在每个SNR下,RSPB定义为信号DOA分辨成功的次数与独立试验总次数的比值,并定义当信号DOA估计的均方根误差在1°以内,则认为信号成功分辨。RSPB变化范围为[0, 1],RSPB越大,分辨性能越好。
|
图 4 RSPB随输入SNR变化曲线 Fig. 4 Curve of RSPB versus input SNR |
从图 4可以看出,本文的方法对信号的DOA有很高的分辨能力,在SNR为0 dB时,分辨概率接近0.9,在SNR大于25 dB后,分辨概率保持为1。
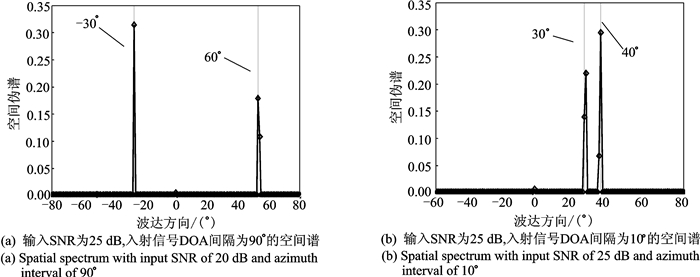
4.4 实验4:宽带入射信号情形下的DOA估计假设入射的宽带信号带限于20~30 kHz,采样频率为100 kHz。阵列数据观测时间分为100段,每段做64点离散傅里叶变换(Discrete Fourier transform,DFT)。考虑:(1)两个等功率的远场宽带信号入射方位角分别为θ1=-30°,θ2=60°,对应的极化参数分别为(26°, 60°)和(45°, 30°),SNR为20 dB,阈值ε2=0.008;(2)两个等功率的远场宽带信号入射方位角分别为θ1=30°,θ2=40°,对应的极化参数分别为(45°, 60°)和(30°, 60°),SNR为20 dB,阈值ε2=0.008。图 5为实验4条件下WJSR方法对DOA的估计结果。从图 5可以看出,本文所提的WJSR方法对宽带信号的DOA估计能得到精度较高的估计结果,估计值和真实值基本重合,能区分两个离得较近的信号。
|
图 5 实验4条件下的空间谱 Fig. 5 Spatial spectrum versus DOAs of experiment 4 |
4.5 实验5:宽带入射信号情形下的分辨概率
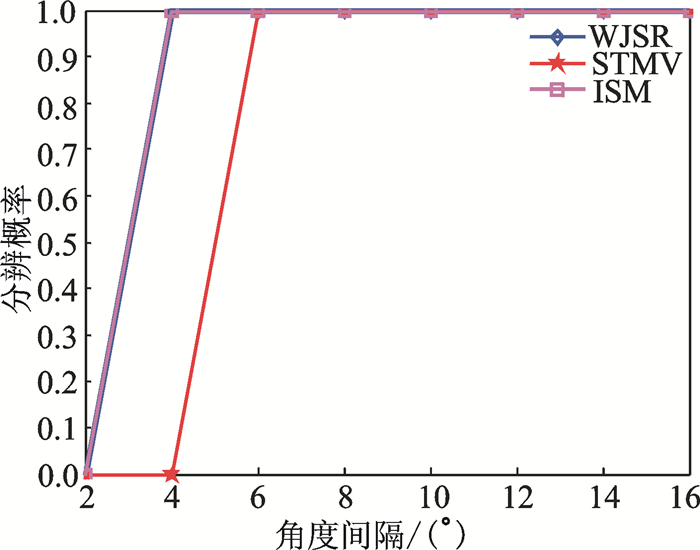
考虑两个等功率的远场宽带信号入射到阵列,入射的方位角角度间隔在2~16°之间变化,变化步长为2°,对应的极化参数分别为(45°, 60°)和(30°, 60°),SNR为25 dB,阈值ε2=0.008。本文将所提的WJSR方法与文献[23]中的非相干子空间方法(Incoherent signal subspace method,ISM),文献[24]中的导向最小方差方法(Steered minimum variance,STMV)进行性能比较。图 6为RSPB随DOA间隔的变化曲线。从图 6可以看出,本文提出的WJSR方法能分辨出距离很近的两个信号,在宽带信号入射DOA间隔大于4°时,RSPB为1。
|
图 6 RSPB随DOA间隔变化曲线 Fig. 6 RSPB versus DOA interval |
5 结束语
本文提出了一种基于COLD阵列的极化-空间域联合稀疏重构信号DOA估计方法。根据COLD阵列的特点构造极化-空间域协方差矩阵,并利用其两个子阵稀疏矢量的共性构造联合稀疏矢量,进而利用l1-范数进行稀疏重构获得信号DOA估计。构造的联合稀疏矢量充分利用了信号的空域稀疏性,为寻求充分稀疏的唯一解提供了保证。仿真结果表明,无论是窄带还是宽带入射信号情形,该方法对距离较近的入射信号都保持着较好的分辨性能,能得到精度较高的DOA估计结果。
| [1] |
尤国红, 邱天爽, 兰天. 脉冲噪声环境下宽带循环平稳信号DOA估计算法[J]. 数据采集与处理, 2012, 27(4): 399-403. You Guohong, Qiu Tianshuang, Lan Tian. DOA estimation algorithm of the wideband cyclostationary signals in impulsive noise environment[J]. Journal of Data Acquisition and Processing, 2012, 27(4): 399-403. |
| [2] |
梁浩, 李小波. 采用单次快拍数据实现信源DOA估计[J]. 数据采集与处理, 2013, 28(1): 58-63. Liang Hao, Li Xiaobo. DOA estimation of signals using one snapshot[J]. Journal of Data Acquisition and Processing, 2013, 28(1): 58-63. |
| [3] |
Wong K T, Yuan X. ″Vector cross-product direction finding″with an electromagnetic vector-sensor of six orthogonally oriented but spatially non-collocating dipoles/loops[J]. IEEE Trans Signal Processing, 2011, 59(1): 160-171. DOI:10.1109/TSP.2010.2084085 |
| [4] |
Wong K T, Zoltowski M D. Closed-form direction finding and polarization estimation with arbitrarily spaced electromagnetic vector-sensors at unknown locations[J]. IEEE Trans Antennas and Propagation, 2000, 48(5): 671-681. DOI:10.1109/8.855485 |
| [5] |
Nehorai A, Paldi E. Vector-sensor array processing for electromagnetic source localization[J]. IEEE Trans Signal Processing, 1994, 42: 376-398. DOI:10.1109/78.275610 |
| [6] |
Wong K T, Zoltowski M D. Uni-vector-sensor ESPRIT for multisource azimuth, elevation, and polarization estimation[J]. IEEE Trans Antennas and Propagation, 1997, 45: 1467-1474. DOI:10.1109/8.633852 |
| [7] |
Hua Y. A pencil-MUSIC algorithm for finding two-dimensional angles and polarizations using crossed dipoles[J]. IEEE Trans Antennas and Propagation, 1993, 41: 370-376. DOI:10.1109/8.233122 |
| [8] |
Schmidt R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans Antennas and Propagation, 1986, 34(3): 276-280. DOI:10.1109/TAP.1986.1143830 |
| [9] |
Li J, Jr Compton R T. Angle and polarization estimation using ESPRIT with a polarization sensitive array[J]. IEEE Trans Antennas and Propagation, 1991, 39(9): 1376-1383. DOI:10.1109/8.99047 |
| [10] |
Donoho D L. Compressed sensing[J]. IEEE Trans Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [11] |
Candès E J, Romberg J, Tao T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Information Theory, 2006, 52(2): 489-509. DOI:10.1109/TIT.2005.862083 |
| [12] |
Donoho D L, Tsaig Y. Extensions of compressed sensing[J]. Signal Processing, 2006, 86(3): 533-548. DOI:10.1016/j.sigpro.2005.05.028 |
| [13] |
Agrawal M, Prassed S. Broadband DOA estimation using ″spatial-only″ modeling of array data[J]. IEEE Trans Signal Processing, 2000, 48(3): 663-670. DOI:10.1109/78.824662 |
| [14] |
Agrawal M, Prassed S. Estimation of direction of arrival of wideband and wideband spread sources[J]. IEEE Trans Signal Processing, 2007, 87(4): 614-622. |
| [15] |
Guo X S, Wan Q, Chang C Q, et al. Source localization using a sparse representation framework to achieve superresolution[J]. Multidim Syst Signal Processing, 2010, 21(4): 391-402. DOI:10.1007/s11045-010-0119-y |
| [16] |
Chow K Y, Lui K S, Lam E Y. Wireless sensor networks scheduling for full angle coverage[J]. Multidim Syst Signal Processing, 2009, 20(2): 101-119. DOI:10.1007/s11045-008-0062-3 |
| [17] |
Tang Z, Balcquière G, Leus G. Aliasing-free wideband beamforming using sparse signal representation[J]. IEEE Trans Signal Processing, 2011, 59(7): 3464-3469. DOI:10.1109/TSP.2011.2140108 |
| [18] |
Gorodnitsky I F, Rao B D. Sparse signal reconstruction from limited data using FOCUSS: A re-weighted minimum norm algorithm[J]. IEEE Trans Signal Processing, 1997, 45(3): 600-616. DOI:10.1109/78.558475 |
| [19] |
Malioutov D, Cetin M, Willsky A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J]. IEEE Trans Signal Processing, 2005, 53(8): 3010-3022. DOI:10.1109/TSP.2005.850882 |
| [20] |
Xu X, Wei X H, Ye Z F. DOA estimation based on sparse signal recovery utilizing weighted l1-norm penalty[J]. IEEE Signal Processing Letters, 2012, 19(3): 155-158. DOI:10.1109/LSP.2012.2183592 |
| [21] |
Hyder M M, Mahata K. Direction-of-arrival estimation using a mixed l2, 0 norm approximation[J]. IEEE Trans Signal Processing, 2010, 58(9): 4646-4655. DOI:10.1109/TSP.2010.2050477 |
| [22] |
Tian Y, Xu H. DOA, power and polarization angle estimation using sparse signal reconstruction with a COLD array[J]. International Journal of Electronics and Communications, 2015, 69: 1606-1612. DOI:10.1016/j.aeue.2015.07.012 |
| [23] |
Wax M, Shan T J, Kailath T. Spatio-temporal spectral analysis by eigenstructure methods[J]. IEEE Trans Acoustics, Speech and Signal Processing, 1984, 32(4): 817-827. DOI:10.1109/TASSP.1984.1164400 |
| [24] |
Krolik J, Swingler D. Multiple broad-band source location using steered covariance matrices[J]. IEEE Trans Acoustics, Speech and Signal Processing, 1989, 37(10): 1481-1494. DOI:10.1109/29.35386 |
 2018, Vol. 33
2018, Vol. 33

