2. 同济大学嵌入式系统与服务计算教育部重点实验室, 上海, 201804
2. Key Laboratory of Embedded Systems and Service Computing, Ministry of Education, Tongji University, Shanghai, 201804, China
主曲线是第一主成分的非线性推广[1],第一主成分是对数据集的一维线性最优描述。主曲线通过将高维数据映射到嵌入在高维空间中的低维流形,以一种新的方式表示数据,使数据分析任务更容易、更准确。由主曲线定义可知:与传统方法相比,用主曲线来分析高维的、高度非线性化、非结构化和高度相关性等特点的数据能取得较好的效果。自20世纪年代以来在国外取得了较快的发展。在数据主曲线提取方面,Trevor Hastie于1989年首次提出了HS主曲线算法[2],除了可以较好地描述非线性数据外,该主曲线另具有自相合以及无参数性等优点,但其仍存在收敛性、估计偏差和模型偏差等问题;为了改善上述问题,1992年Banfield和Raftery提出了BR主曲线算法[3],解决了HS主曲线算法在闭主曲线下曲率过大的问题;Tibshirani针对圆形和椭圆形分布数据的模型偏差问题引入半参数方法[4],重新定义了基于混合模型的主曲线;2000年,Kegl提出PL主曲线算法,引入了有长度约束的主曲线概念[5]。
2002年,Verbeek提出K段主曲线算法,该算法采用逐渐合并局部第一主成分线来构成主曲线[6]。随着主曲线的不断发展与深入应用,学者们发现现有的主曲线算法因为其以第一主成分线作为初始值,已无法处理具有环形分布特征、自相交和分叉等特征的复杂数据。针对此问题,2001年,Delicado提出通过有序连接定向点来估算主曲线,称之为D主曲线算法[7];同年,Verbeek对K段主曲线算法中定义的参数进行了大量改进,提出了软K段主曲线算法[8];2005年,张红云提出将主曲线运用于字符与指纹识别[9];同年,Jochen等提出局部主曲线算法,将数据局部特征引入主曲线的提取中[10]。以上算法的提出较好地解决了对以上数据类型的主曲线提取问题。近些年,主曲线的发展更是如火如荼。2009年,张军平等为解决稀疏和不均匀分布数据的主曲线提取问题提出了自适应约束K段主曲线算法[11],随之又针对具有非恒定分布特征的数据,提出了将数据的黎曼距离与数据的分布密度相结合的主曲线算法[12];同年,Ozertem与Erdogmus从一个新的角度介绍了主曲线和曲面,根据梯度和概率密度估计的海森矩阵重新定义主曲线和曲面(Ozertem and Erdogmus principal curve,OEPC),OEPC算法通过使用基于核密度估计和高斯混合模型的子空间约束均值漂移(Subspace constrained mean shift, SCMS)生成主曲线和主曲面[13];2013年,张红云等提出了基于全局结构的主曲线算法来解决自相交和高度分散数据的主曲线提取问题[14],随之2014年,为了解决大规模复杂形态数据的主曲线提取问题,他们将主曲线推广到粒主曲线[15];2015年,文献[16]针对OEPC算法假定提前获得完整的数据集,并且在计算期间不能将新的数据点添加到数据集的问题,提出了基于SCMS的增量主曲线算法。
随着高速计算机和互联网商业化的飞速发展,存储在数据库中的海量数据的分布形式越来越多样,这导致用传统的主曲线分析算法来处理这些数据不能给出理想的结果。针对海量复杂数据,2017年胡作梁和张红云提出了基于MapReduce框架的分布式软K段主曲线算法(Distributed soft K-segments principal curve, DisSKPC)[17],大大提升了主曲线对复杂数据的处理速度。但对于不同类别的数据类簇相互包含的复杂数据,现有的软K段主曲线算法仍无法较好地处理,因此迫切需要新理论、新方法来解决该类复杂数据的主曲线学习问题,而粒计算是研究如何模拟人类思维,采用多层次、多粒度的思维方式、问题求解方法来解决复杂问题的有效工具。因此,本文研究将粒计算引入复杂数据的主曲线学习中,探索多粒度主曲线学习方法。
本文针对传统主曲线学习在处理复杂性数据中存在的问题和困难,探索采用粒计算的粒化策略,根据数据相似性、近似性和功能性来实现对数据的粒化拆分和数据转换,形成数据片段(即局部数据);基于主曲线理论和方法,对每类局部数据提取主曲线;采用从局部到全局的,自底向上的策略进行多粒度主曲线提取,最终形成数据完整的主曲线分布。
1 相关工作 1.1 主曲线定义主曲线是第一主成分的非线性推广,在1988年由Trevor Hastie首次提出,他将主曲线定义成一条通过数据云或者分布“中间”且满足自相合的光滑曲线。
HSPC定义 如果光滑曲线f(λ)满足:
(1) f(λ)不自相交;
(2) 在任何有界Rd子集内;f(λ)是有限长度的;
(3) f(λ)是自相合的,即f(λ)=E(X|λf(x)=λ), 则称f(λ)为X的一条主曲线。其中λf(x)为数据点x投影到曲线f(λ)上λ点的值,即
| $ {\lambda _f}(\boldsymbol{x}) = \sup\{ \lambda :\left\| {\boldsymbol{x}-f(\lambda )} \right\| = \mathop {\inf }\limits_\tau \left\| {\boldsymbol{x}-f(\tau )} \right\|\} $ |
Verbeek认为HS主曲线算法及其改进算法(如BR主曲线,T主曲线和多边形主曲线算法等)存在一个共同的问题,即把数据的第一主成分作为初始化线,没有考虑数据的局部结构特点。因此,当数据分布在弯曲度较大或相交曲线周围时,以上算法给出的最终主曲线分布并不能正确反映数据的真实拓扑结构。而软K段主曲线算法能克服“局部模型”的缺点,可以较好地提取出分布在弯曲度很大或相交曲线周围的数据的主曲线,因此许多学者将该算法应用于指纹和字符识别[18-20]。由于通常k≤n,所以算法的总时间复杂度为O(kn2),因需要预先存储两两点之间的距离(对称矩阵,如果使用稀疏矩阵存储,可以节省一半的存储空间),所以总的空间复杂为O(n2),其中k为拟合的线段数,n为数据总数。
随着信息技术的高速发展,数据收集和数据存储技术的快速进步使得各行各业积累了海量复杂的数据,单纯依靠软K段主曲线算法也难以很好地解决现存的一些复杂数据的主曲线提取问题。本文考虑引入粒计算的粒化思想,完成复杂数据的预处理工作。
1.2 粒化粒化是利用指定的粒化策略将复杂数据粒化为信息粒的一个过程,为粒计算的基本问题之一。根据不同信息特征和用户需求目标,采用不同的信息粒化方法。常用的粒化方法有基于二元关系的粒化、基于聚类的粒化、基于集值数据的粒化和基于缺省数据的粒化等[21]。
在现有的粒化方法中,聚类算法是一种常用且有效的数据粒化方法,它通过有机地聚集数据集中的对象,以形成互不相交的数据类型。根据数据集的取值类型划分,目前基于聚类的信息粒化方法主要研究数值型、名义型以及混合型3种数据。而本课题着重解决数值型的复杂数据粒化问题。针对数值型的复杂数据,虽然基于聚类的粒化方法能够处理部分数据集,但对于不同类别的数据类簇相互包含的数值型复杂数据的信息粒化研究还不够充分。探讨这些问题,对于粒化算法的研究具有重要的意义。在过去数十年里,谱聚类算法在数据聚类和图像分割中展现出明显的优势。2002年,Hagen和Kahng[22]提出基于谱图划分理论的谱聚类方法,后因Ng等[23]对其理论基础的完善,使之成为目前数据挖掘领域最常用的聚类算法之一。该算法的主要思想是以谱图理论为基础,通过对数据样本的相似性矩阵进行特征分解,将高维数据映射到低维特征向量空间,然后在特征向量空间中对数据点进行聚类。与其他分类方法相比,谱聚类因其高维数据空间向低维特征向量空间映射的特性,使之能在避免“维度灾难”的前提下处理非凸样本空间,并且保证全局最优收敛。
本文着眼于处理复杂性数值数据,合理选择粒计算中的谱聚类粒化算法,对数据进行预处理,并针对每个粒数据提取主曲线,提出了一种新的数据处理方法。该方法能够从理论上完善数据处理中复杂性数据的表示以及分析等问题的研究,并在实际应用中扩展主曲线的应用领域,推动主曲线理论在数据挖掘、机器学习和知识发现领域的发展。
2 基于粒计算的复杂数据多粒度主曲线提取算法 2.1 基于TNN的谱聚类算法Chen等[24]提出利用t最近邻方法(T-nearest neighbor, TNN)构建相似度矩阵S,从而避免了处理复杂数据时稠密相似度矩阵的存储问题,更减少了算法运行时所需的时间、空间以及计算的复杂度,可见基于TNN的谱聚类算法在处理复杂数据上具有很大优势。其主要算法流程为:
(1) 构造稀疏相似性矩阵。针对每个数据样本点xi,计算其与其他每一个样本点的相似性距离并插入大小为t的最大堆Hi中,然后得到与xi最相似的t个样本点,作为稀疏相似性矩阵S的第i行。相似性距离计算方式如式(1),其中,σ是一个控制Sij随xi和xj之间距离变化速度的缩放因子。
| $ {S_{ij}} = \exp (-\frac{{{{\left\| {{\boldsymbol{x}_i}-{\boldsymbol{x}_j}} \right\|}^2}}}{{2{\sigma ^2}}}) $ | (1) |
(2) 利用式(2)计算Laplacian矩阵。其中,D是一个对角矩阵:
| $ \boldsymbol{L} = \boldsymbol{I}-{\boldsymbol{D}^{-1/2}}\boldsymbol{S}{\boldsymbol{D}^{-1/2}} $ | (2) |
(3) 选取Laplacian矩阵的前k个最大特征值,将数据映射到低维特征向量空间。
(4) 在低维特征向量空间中对数据点使用K-means聚类算法进行聚类。
2.2 软K段主曲线算法Verbeek采用局部主成分方法得到k条线段的方法重新定义了软K段主曲线算法,并依据光滑性连接k条线段形成最终的主曲线,其与数据间距离均方差较小,能够更真实地反映数据的原始分布形态。其算法流程为:
(1) 初始化。输入数据样本点;计算第一主成分线;输入k_max。
(2) 插入一条新的线段。如果k>k_max,则流程结束。否则,计算点xq,求出点xq的Voronoi域,Voronoi域为
| $ {V_q} = \{ \left. {\boldsymbol{x} \in \boldsymbol{X}} \right|\left\| {\boldsymbol{x}-{\boldsymbol{x}_q}} \right\| \le \min d(\boldsymbol{x}, {s_j}), j = 1, 2, \cdots, k\} $ | (3) |
计算Vq的第一主成分线,新插入线段为3σ,第一主成分线的方差为σ2。k=k+1,令sk为新插入线段,sk的Voronoi域为Vk=Φ。
(3) 调整新线段与其他线段。定义每条线段原来的Voronoi域(V1, V2, …, Vk);求出每条线段新的Voronoi域(V′1, V2′, …, Vk′);对比(V1, V2, …, Vk)与(V′1, V2′, …, Vk′)域是否相同。如果不同,计算V′j(j=1, 2, …, k)所有的第一主成分线,并把(V′1, V2′, …, Vk′)赋值给(V1, V2, …, Vk),继续第(2)步;否则,进行第(4)步。
(4) 构造优化。将k条线段当做哈密顿回路问题求解,并进行优化,得到一条通过各个端点的最优曲线。计算目标函数OF是否最小,如果OF最小,则程序结束,否则返回第(2)步。
2.3 基于谱聚类的软K段主曲线算法本算法将基于TNN的谱聚类算法和软K段算法有效地融合,提出了一种新的基于粒计算的复杂数据多粒度主曲线提取算法(T-nearest-neighbors spectral clustering and soft K-segmeuts, TNNSC_SK),并且作了以下改进:(1)对谱聚类算法在第(2)步提出拐点估计方法来自动确定粒的个数,有效避免了自定义粒子数目时引起的“错误传播”;(2)对软K段主曲线算法在第(3)步做了改进,原软K段主曲线算法是基于把所有主曲线Hamilton路径算法全部相连,但对于一些复杂数据,所有线段完全连接是不合适的,因此这里设定第(3)步中的条件以删除假边;(3)原软K段主曲线算法选择目标函数OF达到最小作为主曲线构造过程的终止条件。但是在构造多粒度全局主曲线时,单纯的选择这些条件,容易使最终的主曲线产生过拟合现象,改进的算法在第(4)步中消除部分过拟合的线段,使最终形成多粒度全局主曲线更符合数据的原始分布形态。
TNNSC_SK:基于谱聚类的软K段主曲线算法伪码可描述为
(1) 输入:数据点xi
(2) 输出:数据点的主曲线连接矩阵及段的端点等
(3) 函数:gen_nn_distance(ThreeCircles, num_neighbors, block_size, 0)
计算相似度矩阵;
输出相似度矩阵文件:NN_sym_distance.mat
(4) 函数:sc1(A, sigma, num_clusters)
谱聚类;
输出聚类的标签矩阵:cluster_labels
(5) 函数:k_seg_soft(X, k_max, alpha, lambda, INT_PLOT)
软K段主曲线算法;
输出主曲线的连接矩阵及段的端点等:[edges, vertices, of, y, mm, mm2]
步骤可详细描述为:
(1) 利用谱聚类进行数据特征提取。输入所有数据点xi,计算其到所有数据点的距离, 即
| $ {\left\| {{\boldsymbol{x}_i}-{\boldsymbol{x}_j}} \right\|^2} = {\left\| {{\boldsymbol{x}_i}} \right\|^2} + {\left\| {{\boldsymbol{x}_j}} \right\|^2}-2\boldsymbol{x}_i^T{\boldsymbol{x}_j} $ | (4) |
利用相似度函数公式(5)得到数据集的相似度矩阵,其中选择参数σi[25],σi=‖xi-xit‖,xit为通过排序xi的
| $ {S_{ij}} = \exp (-\frac{{{{\left\| {{\boldsymbol{x}_i}-{\boldsymbol{x}_j}} \right\|}^2}}}{{2{\sigma _i}{\sigma _j}}}) $ | (5) |
计算Laplacian矩阵,选取Laplacian矩阵的前k个最大的特征值,得到特征向量v1, v2, …, vk,构造矩阵V=[v1, v2, …, vk]∈Rk×k。
(2) 利用拐点的除斜率确定粒的数目。基于快速搜索和密度峰的聚类算法(Clustering by fast search and find of density peaks,CFSFDP)[26]是2014年发表在Science杂志上的一种聚类算法,该算法为每个样本点引入两个属性局部密度ρi和距离δi。基于CFSFDP算法提出的两个属性值引入一个新的变量γi,称为决策属性,其计算公式为
| $ {\gamma _i} = {\rho _i}*{\delta _i} $ | (6) |
通过相邻数据的决策属性相减的方式获得减斜率,再把相邻减斜率相除得到除斜率,这里把除斜率比左右相邻点都大的点所在的序号作为拐点,也就是最后的聚类数目cluster_num。最后将cluster_num作为聚类的个数传入k-means方法,输出样本的粒化标签向量cluster_labels。
(3) 消除构造Hamilton路径中的假边。根据标签向量cluster_labels输入单粒度的数据,利用软K段算法进行单粒度主曲线的提取,产生s1, s2, …,sk线段,然后使用贪婪算法进行Hamilton路径的构造,产生连线e1, e2,…, ek-1。虽设有代价函数C(ei)=s(ei)+λ a(ei),其中ei为连接两个子图端点的边,s(ei)为边ei的长度,但仍避免不了假边的出现。因此作以下改进:对e1, e2,…, ek-1检查ei连接的主干线si,si+1,将si,si+1被ei连接的两端点的Voronoi域点形成一个点集合,计算域中每个点相对ei边的Voronoi′域,并计算Voronoi′域内点的数目/ei线段长度,定义为dei,若dei大于给定的经验值,则判断ei为假边,并从e1, e2, …, ek-1中消除。
(4) 构造多粒度全局主曲线。输入所有粒的s1, s2, …,sk与e1, e2, …, ek-1线段,利用局部到全局的策略完成主曲线的多粒度提取过程,即使当目标函数OF达到最小,也不能确保最终的主曲线最接近数据的原始分布,往往出现过拟合现象。
| $ OF = N\lg s + \sum\limits_{i = 1}^k {\sum\limits_{i \in {V_i}} {d{{({\boldsymbol{x}_i}, s)}^2}/(2{\sigma ^2})} } $ | (7) |
据此提出以下改进:分别计算s1, s2, …,sk中任意两个线段间的距离。如si,计算其余线段两端点到该线的投影距离为dsisj,若dsisj小于λσ2(其中λ为自定义参数,σ2为噪声方差),即考虑删除si与sj中较短的线段。
2.4 算法复杂度分析在TNNSC_SK算法中,计算Laplacian矩阵的计算开销较小,kmeans算法以及改进后的软K段主曲线算法的复杂度变化相对较小,因此这里不再讨论。
通过计算所有样本点之间的相互距离,最后得到与xi最为相似的t个样本点,在t个样本点的堆中插入或者删除1个元素的时间复杂度为O(logt),因此该步骤的时间复杂度为:O(n2d+n2logt);该步骤需要维护n个大小为t的样本堆,因此空间复杂度为:O(nt)。其中n为数据总数,d为数据维数,t为最近邻数目。
3 实验及分析使用本文提出的TNNSC_SK算法,在2个公开数据集(Twomoons,Spiral)和2个人工数据集(DisorderThreeCircles,ThreeCircle)上进行了测试。计算机CPU为Intel(R) Xeon(R) CPU E5-2630 v2 @ 2.60 GHz,内存8 GB,操作系统Windows 7,操作软件为MATLAB R2014a。
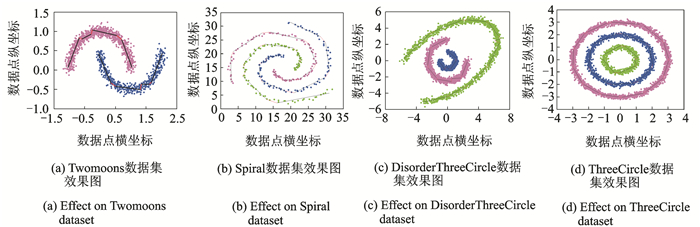
3.1 有效性分析对于4类数据集,TNNSC_SK算法的实验结果如图 1所示,其中不同的颜色代表不同的粒化结果,黑色线段与红色线段共同组成每个粒的主曲线。可见,本文提出的算法能比较完好地拟合出复杂数据的分布形态。
|
图 1 TNNSC_SK算法在不同数据集上的效果图 Fig. 1 Effect of TNNSC_SK on different datasets |
3.2 对比性分析
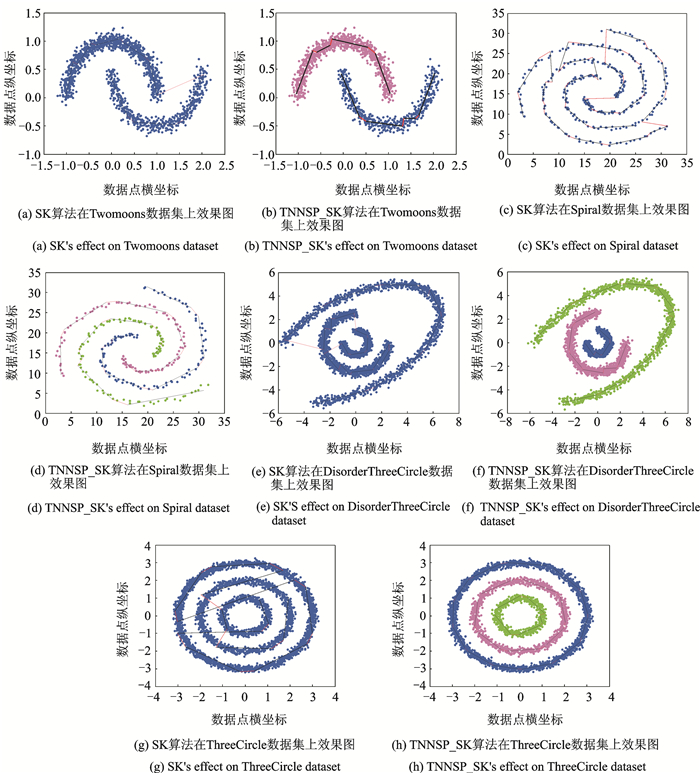
通过5组对比实验来验证所提算法的可行性。5组实验分别是在Twomoons,Spiral,DisorderThreeCircles和ThreeCircles四个数据集上对比TNNSC_SK算法和软K段主曲线算法(SK)算法,结果如图 2所示; 以及在Spiral数据集上对比TNNSC_SK算法与DisSKPC算法,结果如图 3所示。其中图 2 (a, c, e, g)为SK算法的运行结果,图 2(b, d, f, h)为TNNSC_SK算法的运行结果,不同的颜色代表不同的粒数据。从图 2(a, c, e, g)4个图中都可看出SK算法存在过拟合现象,而且只有主曲线无法区分复杂数据的分布种类。而从图 2(b, d, f, h)可看出,TNNSC_SK算法把复杂数据粒化成多个粒再分别进行主曲线的提取,有效避免了不同粒之间过拟合线段的产生。
|
图 2 SK和TNNSC_SK算法在不同数据集上的效果对比图 Fig. 2 Effect comparison of SK and TNNSC_SK on different datasets |
|
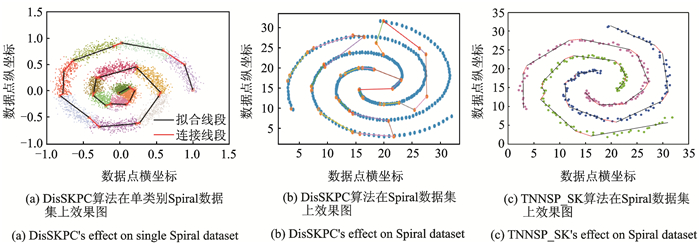
图 3 DisSKPC和TNNSC_SK效果对比图 Fig. 3 Effect comparison of DisSKPC and TNNSC_SK |
从文献[17]中得知DisSKPC算法主要针对复杂数据的海量问题,如图 3(a)显示,在处理复杂的单螺旋Spiral数据集上该算法效果极佳,能较真实地描绘出数据的原始分布形态;但对于多螺旋Spiral数据集,DisSKPC算法处理结果如图 3(b),可看出存在过拟合及假边现象,而且无法区分数据的分布种类,TNNSC_SK算法处理结果如图 3(c),消除了图 3(b)在主曲线提取时的问题,并且主曲线的分布更符合数据的真实形态。
综上所述,TNNSC_SK算法相比于传统的SK算法以及SK算法的DisSKPC改进算法,能更好地拟合出复杂数据的原始分布形态。
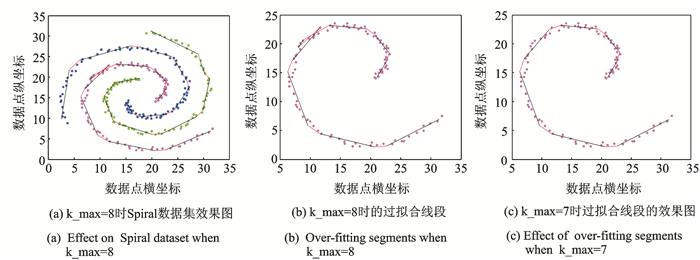
3.3 目标函数OF对多粒度主曲线提取时的影响针对软K段主曲线算法的结束条件——目标函数OF对多粒度主曲线提取时的影响,作了如下实验。如表 1以Spiral数据集粒化后的一个粒(图 4(a)中的紫色粒)为例,当OF值达到最小值0.164 5时,建议的最大主曲线段数k_max为8,但当k_max设为8时,在使用本文所提算法对该粒进行主曲线提取的过程中,出现了过拟合现象,如图 4(b)。因此单纯依靠目标函数OF值达到最小作为算法的终止条件是不可靠的。
|
图 4 TNNSC_SK优化对比效果图 Fig. 4 Effect optimization of TNNSC_SK |
| 表 1 目标函数OF值 Tab. 1 Value of OF |
本文在算法2.3的第(4)步中,对该问题进行了优化,以删除图 4(b)中黑色的过拟合边,经过实验达到了图 4(c)的结果,此时OF值为0.201 8,k_max设为7。根据图 4的效果图可知,单纯依靠目标函数或k_max作为算法终止条件会导致过拟合现象,而结合本文提出的优化算法可以有效地解决该问题。并且根据2.3中第3步消除假边的优化方法,可以有效地删除图 4(b)中交叉的两条红色假边。
4 结束语本文针对复杂的数值数据设计并实现了基于粒计算的复杂数据多粒度主曲线提取算法,并在确定粒子数目、消除假边和过拟合线段上作了优化。通过有效性、对比性以及目标函数OF等多个角度进行了实验,结果表明本文所提算法在复杂形状数据的主曲线提取上明显优于软K段算法,能更好地拟合出复杂数据的原始分布形态。但本算法也有待改进的地方,如在构造多粒度全局主曲线时,对于如何处理过拟合边仍需要讨论,这在下一步工作中将进行深入研究。主曲线算法以一种非监督的方式揭示数据的分布规律,在机器学习领域有重要地位,而本文提出的方法为处理复杂数据提供了一种新的可行且有效的解决方案。
| [1] |
Baldi P, Hornik K. Neural networks and principal component analysis: Learning from examples without local minima[J]. Neural Networks, 1989, 2(1): 53-58. DOI:10.1016/0893-6080(89)90014-2 |
| [2] |
Hastie T, Stuetzle W. Principal curves[J]. Journal of the American Statistical Association, 1989, 84(406): 502-516. DOI:10.1080/01621459.1989.10478797 |
| [3] |
Banfield J D, Raftery A E. Ice floe identification in satellite images using mathematical morphology and clustering about principal curves[J]. Journal of the American Statistical Association, 1992, 87(417): 7-16. DOI:10.1080/01621459.1992.10475169 |
| [4] |
Tibshirani R. Principal curves revisited[J]. Statistics and Computing, 1992, 2(4): 183-190. DOI:10.1007/BF01889678 |
| [5] |
Kegl B, Krzyzak A, Linder T, et al. Learning and design of principal curves[J]. Pattern Analysis & Machine Intelligence IEEE Transactions on, 2000, 22(3): 281-297. |
| [6] |
Verbeek J J, Vlassis N, Se B. A k-segments algorithm for finding principal curves[J]. Pattern Recognition Letters, 2002, 23(8): 1009-1017. DOI:10.1016/S0167-8655(02)00032-6 |
| [7] |
Delicado P. Another look at principal curves and surfaces[J]. Journal of Multivariate Analysis, 2001, 77(1): 84-116. DOI:10.1006/jmva.2000.1917 |
| [8] |
Verbeek J J, Vlassis N A, Kröse B J A. A soft k-segments algorithm for principal curves[M]. Berlin, Heidelberg: Springer, 2001: 450-456.
|
| [9] |
张红云. 基于主曲线的脱机手写字符识别的研究[D]. 上海: 同济大学, 2005. Zhang Hongyun. Research on off-line handwritten digit recognition based on principal curves [D]. Shanghai: Tongji University, 2005. |
| [10] |
Einbeck J, Tutz G, Evers L. Local principal curves[J]. Statistics and Computing, 2005, 15(4): 301-313. DOI:10.1007/s11222-005-4073-8 |
| [11] |
Zhang J, Chen D, Kruger U. Adaptive constraint k-segment principal curves for intelligent transportation systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 9(4): 666-677. |
| [12] |
Zhang J, Wang X, Kruger U, et al. Principal curve algorithms for partitioning high-dimensional data spaces[J]. IEEE Transactions on Neural Networks, 2011, 22(3): 367-380. DOI:10.1109/TNN.2010.2100408 |
| [13] |
Ozertem U, Erdogmus D. Locally defined principal curves and surfaces[J]. Journal of Machine Learning Research, 2011, 12(4): 1249-1286. |
| [14] |
Zhang H, Pedrycz W, Miao D, et al. A global structure-based algorithm for detecting the principal graph from complex data[J]. Pattern Recognition, 2013, 46(6): 1638-1647. DOI:10.1016/j.patcog.2012.11.015 |
| [15] |
Zhang H, Pedrycz W, Miao D, et al. From principal curves to granular principal curves[J]. IEEE Transactions on Cybernetics, 2014, 44(6): 748-760. DOI:10.1109/TCYB.2013.2270294 |
| [16] |
Ghassabeh Y A, Rudzicz F. Incremental algorithm for finding principal curves[J]. IET Signal Processing, 2015, 9(7): 521-528. DOI:10.1049/iet-spr.2014.0347 |
| [17] |
胡作梁, 张红云. 基于MapReduce框架的分布式软K段主曲线算法[J]. 数据采集与处理, 2017, 32(3): 507-515. Hu Zuoliang, Zhang Hongyun. Distributed soft k-segments algorithm for principal curves based on mapreduce[J]. Journal of Data Acquisition and Processing, 2017, 32(3): 507-515. |
| [18] |
张红云, 苗夺谦, 傅文杰. 基于改进的GPL主曲线算法的指纹特征分析与提取[J]. 模式识别与人工智能, 2007, 20(6): 763-769. Zhang Hongyun, Miao Duoqian, Fu Wenjie. Analysis and extraction of fingerprint minutiae based on improved GPL principal curve algorithm[J]. Pattern Recognition and Artificial Intelligence, 2007, 20(6): 763-769. |
| [19] |
Yang M, Liao Z W. The skeletonization research of low-quality Chinese characters based on principal curves [C] // Machine Learning and Cybernetics, 2009 International Conference. Baoding, China: Institute of Electrical and Electronics Engineers, 2009:3238-3241.
|
| [20] |
焦娜. 改进的软K段主曲线算法及其在指纹骨架提取中的应用[J]. 数据采集与处理, 2015, 30(5): 1070-1077. Jiao Na. Improved soft K-segments algorithm for principal curves and its applications on fingerprint skeletonization extraction[J]. Journal of Data Acquisition and Processing, 2015, 30(5): 1070-1077. |
| [21] |
钱宇华. 复杂数据的粒化机理与数据建模[D]. 太原: 山西大学, 2011. Qian Yuhua. Granulation mechanism and data modeling of complex data[D]. Taiyuan: Shanxi University, 2011. |
| [22] |
Hagen L, Kahng A B. New spectral methods for ratio cut partitioning and clustering[J]. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, 2002, 11(9): 1074-1085. |
| [23] |
Ng A Y, Jordan M I, Weiss Y. On spectral clustering: Analysis and an algorithm[J]. Proceedings of Advances in Neural Information Processing Systems, 2002, 14: 849-856. |
| [24] |
Chen W Y, Song Y, Bai H, et al. Parallel spectral clustering in distributed systems[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2011, 33(3): 568-586. |
| [25] |
Zelnik-Manor L. Self-tuning spectral clustering[J]. Advances in Neural Information Processing Systems, 2004, 17: 1601-1608. |
| [26] |
Rodriguez A, Laio A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496. DOI:10.1126/science.1242072 |
 2018, Vol. 33
2018, Vol. 33

