引言

支持向量机(Support vector machines, SVMs)是基本机器学习模型和有效的数据挖掘方法之一。核SVM通过引入核技巧实现应用线性方法来学习非线性关系的途径, 但SVM的求解是一个二次规划问题, 时间复杂度为O(n³), 空间复杂度为O(n²), 其中n为训练集规模^[1-2], 这成为发展大规模SVM的主要瓶颈。

为发展大规模SVM, 文献[3]提出基于核矩阵近似的并行SVM算法, 引入核缓存策略来并行计算核矩阵, 数据分块数设为l/d, 其中, l为训练集规模, d为核缓存区大小。近年来, 应用随机特征映射近似核方法的研究引起了广泛关注。Rahimi等人提出利用随机傅里叶特征映射近似高斯核函数，进而在显式随机特征空间中应用线性SVM来一致逼近核诱导特征空间中的高斯核SVM^[4-5], 成为提升SVM可扩展性的有效方法。Feng等人提出一种新的随机特征映射方法^[6], 利用有符号循环随机矩阵代替无结构随机矩阵来投影数据。该方向的工作进一步发展了有效的近似方法, 时间复杂度可降至与数据规模呈对数线性, 同时也发展了大规模核方法^[7]。文献[8]通过引入半宽因子，构造高斯区间核SVM模型，发展了针对区间型数据的高效分类方法。

交替方向乘子法(Alternating direction method of multipliers, ADMM)提供一个简单且强大的并行/分布式计算框架, 可将大规模问题分解为多个小规模子问题, 进而相互协调且并行一致地求解原问题^[9]。在该框架下, 文献[10]提出基于并行/分布式ADMM的线性SVM算法。该算法中的数据分块数依据经验来选择, 没有探讨数据分块数对模型泛化性和计算效率的影响。文献[11]将随机特征映射与并行/分布式ADMM相结合, 提出基于核方法统计模型的大规模训练框架。该框架适合多种统计学习任务, 分块数目经验地取为D/d, 其中, D为随机特征维度, d为训练数据维度。矩阵分解与填充广泛应用于推荐系统中, 分布式矩阵分解得到了广泛关注。Yu等人^[12]研究随机ADMM框架下分布式求解矩阵分解问题, 矩阵划分块数与集群节点个数相同, 没有讨论分块数目对均方根误差的影响。Zhang等人^[13]提出基于分解法的可扩展核岭回归算法, 通过适当的参数调节，只要分块数目不是太多，该方法可以提高计算速度，保持统计最优性, 进而得到有效的一致模型估计量。

已有的并行/分布式机器学习方法中, 数据分块工作没有明确的分块数选择准则, 也缺乏基本的理论保证。针对这一问题, 提出大规模并行效率敏感的数据分块数选择准则。该准则以并行/分布式机器学习的泛化误差与数据分块数之间的关系为基础, 折衷泛化误差与并行效率, 可在保证并行/分布式机器学习测试精度的条件下, 提高计算效率。在ADMM框架下的随机傅里叶特征空间中, 采用所提出的数据分块数选择准则实现一个大规模支持向量机模型。实验结果表明, 该准则在保证大规模支持向量机测试精度的同时, 仍可进一步提高计算效率。

1 相关工作 1.1 交替方向乘子法

当目标函数满足可加性时, 并行/分布式ADMM等式约束问题^[9]为

$ \mathop {\min }\limits_{\mathit{\boldsymbol{\omega }},\mathit{\boldsymbol{z}}} \sum\limits_{i = 1}^B {{f_i}\left( {{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{\omega }}_i} - {\mathit{\boldsymbol{b}}_i}} \right) + g\left( \mathit{\boldsymbol{\upsilon }} \right)} ,{\rm{s}}.\;{\rm{t}}.\;{\mathit{\boldsymbol{\omega }}_i} - \mathit{\boldsymbol{\upsilon }} = 0,\;\;\;\;i = 1, \cdots ,B $

其中:ω_i∈R^d, υ∈R^d, A_i∈R^n_i×d, b_i∈R^n_i且$\sum\limits_{i = 1}^B {{n_i} = N} $, N为数据规模。缩放形式的增广拉格朗日函数为

$ {\mathscr{L}_i}\left( {{\mathit{\boldsymbol{\omega }}_i},\mathit{\boldsymbol{\upsilon }},{\mathit{\boldsymbol{u}}_i}} \right) = {f_i}\left( {{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{\omega }}_i} - {\mathit{\boldsymbol{b}}_i}} \right) + g\left( \mathit{\boldsymbol{\upsilon }} \right) + \frac{\rho }{2}\left\| {{\mathit{\boldsymbol{\omega }}_i} - \mathit{\boldsymbol{\upsilon }} + {\mathit{\boldsymbol{u}}_i}} \right\|_2^2 - \frac{\rho }{2}\left\| {{\mathit{\boldsymbol{u}}_i}} \right\|_2^2 $

其中:ρ>0为惩罚系数, u_i=y/ρ为缩放对偶变量，y为拉格朗日乘子向量。每个从进程并行更新局部变量ω_i, u_i。主进程汇聚ω_i, u_i, 更新全局变量υ, 并广播给从进程。并行/分布式ADMM交替优化过程见算法1。

算法1  分布式交替方向乘子法(D-ADMM)

输入：函数f, g, 矩阵A, 分块数备选集B, 惩罚系数ρ>0。

(1) 初始化:ω⁰, υ⁰, y⁰;

(2) repeat

(3) $\mathit{\boldsymbol{\omega }}_i^{k + 1}{\bf{:}}\; = \mathop {{\rm{argmin}}}\limits_{{\mathit{\boldsymbol{\omega }}_i}} {f_i}\left( {{\mathit{\boldsymbol{A}}_i}{\mathit{\boldsymbol{\omega }}_i} - {\mathit{\boldsymbol{b}}_i}} \right) + \frac{\rho }{2}\left\| {{\mathit{\boldsymbol{\omega }}_i} - \mathit{\boldsymbol{\upsilon }} + \mathit{\boldsymbol{u}}_i^k} \right\|_2^2$;

(4) ${\mathit{\boldsymbol{\upsilon }}^{k + 1}}{\bf{:}}\; = \mathop {{\rm{argmin}}}\limits_\mathit{\boldsymbol{\upsilon }} \left( \mathit{\boldsymbol{\upsilon }} \right) + \frac{{B\rho }}{2}\left\| {\mathit{\boldsymbol{\upsilon }} - {{\mathit{\boldsymbol{\bar \omega }}}^{k + 1}} - {{\mathit{\boldsymbol{\bar u}}}^k}} \right\|_2^2$;

(5) u_i^k+1:=u_i^k+ω_i^k+1-υ^k+1;

(6) until满足终止条件。

输出：ω^*, υ^*, y^*。

D-ADMM的终止条件为

$ 原残差{\left( {\sum\limits_{i = 1}^B {\left\| {\mathit{\boldsymbol{\omega }}_i^{k + 1} - {\mathit{\boldsymbol{\upsilon }}^{k + 1}}} \right\|_2^2} } \right)^{1/2}} \le {\varepsilon ^{{\rm{pri}}}}\;且对偶残差\;\rho \sqrt N {\left\| {{\mathit{\boldsymbol{\upsilon }}^{k + 1}} - {\mathit{\boldsymbol{\upsilon }}^k}} \right\|_2} \le {\varepsilon ^{{\rm{dual}}}} $

其中:ε^pri>0, ε^dual>0分别为原问题和对偶可行性条件的误差, 定义为

$ {\varepsilon ^{{\rm{pri}}}} = \sqrt N {\varepsilon ^{{\rm{abs}}}} + {\varepsilon ^{{\rm{rel}}}}\max \left\{ {{{\left\| {{{\mathit{\boldsymbol{\bar \omega }}}^{k + 1}}} \right\|}_2},{{\left\| \mathit{\boldsymbol{\upsilon }} \right\|}_2}} \right\},{\varepsilon ^{{\rm{dual}}}} = \sqrt N {\varepsilon ^{{\rm{abs}}}} + {\varepsilon ^{{\rm{rel}}}}\rho {\left\| {{{\mathit{\boldsymbol{\bar u}}}^{k + 1}}} \right\|_2} $

其中:ε^abs>0, ε^rel>0分别为绝对误差和相对误差^[9]。

满足如下两个假设的条件时, D-ADMM收敛^{[9, 14]}。

假设1  扩展实值函数f:Rⁿ→R∪{+∞}, g:R^m→R∪{+∞}是封闭、适定且凸的^[15]。

假设2  增广拉格朗日函数$\mathscr{L}$存在鞍点。

1.2 随机傅里叶特征映射

高斯核函数是一种通用的平移不变核, 定义为

$ k\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \exp \left( { - \gamma \left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right\|_2^2} \right) $

(1)

式中γ=1/2σ²。

可通过高斯核函数的傅里叶逆变换得到ω的概率密度函数p(ω), ω~正态分布$\mathscr{N}$(0, 2γI), 其中I为单位矩阵。易知

$ k\left( {\mathit{\boldsymbol{x}},\mathit{\boldsymbol{y}}} \right) = \mathit{\boldsymbol{E}}\left[ {{{\rm{e}}^{ - {\mathit{\boldsymbol{\omega }}^{\rm{T}}}\left( {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right)}}} \right] = {\mathit{\boldsymbol{E}}_{\omega ,b}}\left[ {\sqrt 2 \cos \left( {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{x}} + b} \right)\sqrt 2 \cos \left( {{\mathit{\boldsymbol{\omega }}^{\rm{T}}}\mathit{\boldsymbol{y}} + b} \right)} \right] $

令T_{ω, b}(x)=$\sqrt 2 $cos(ω^Tx+b)得k(x, y)=E[〈T_{ω, b}(x), T_{ω, b}(y)〉]。

可见, 〈T_{ω, b}(x), T_{ω, b}(y)〉是高斯核函数(1)的无偏估计。通过标准蒙特卡洛积分近似高斯核, 构造如下随机傅里叶特征映射^[4-5]

$ \mathit{\Phi }:x \to \sqrt {\frac{2}{D}} \cos \left( {\mathit{\boldsymbol{Tx}} + \mathit{\boldsymbol{b}}} \right) $

(2)

式中:D为随机特征维度, 高斯随机矩阵T∈R^D×d, T_i~$\mathscr{N}$(0, 2γI), b为随机向量, b_i~均匀分布U(-π, π), i=1, …, D。则k(x, y)=E[〈Φ(x), Φ(y)〉]。

2 并行/分布式机器学习模型泛化误差分析

本节推导并行/分布式机器学习模型数据分块数与泛化误差之间的关系。

不失一般性, 界定以下假设条件:

假设3  f^*∈C(X)且‖f^*‖_∞≤M。其中, C(X)是X上的连续函数空间, ‖·‖_∞为上确界范数。

假设4  损失函数$\mathcal{l}$(·)为非负L-Lipschiz连续的凸函数。${\mathscr{H}}_K$是一再生核Hilbert空间(RKHS)。对任意f₁, f₂∈${\mathscr{H}}_K$, 存在常数L>0, 使得

$ \left| {l\left( {{\mathit{\boldsymbol{f}}_1},\mathit{\boldsymbol{z}}} \right) - l\left( {{\mathit{\boldsymbol{f}}_2},\mathit{\boldsymbol{z}}} \right)} \right| \le {L_1}{\left\| {{\mathit{\boldsymbol{f}}_1} - {\mathit{\boldsymbol{f}}_2}} \right\|_\infty } $

假设5  任意g∈C(X), ε>0, 存在f∈${\mathscr{H}}_K$, 使得‖f-g‖_∞ < ε。令B_R={f∈${\mathscr{H}}_K$, ‖f‖_∞≤R}, R>0。存在常数C₀, s>0, 使得

$ {\mathscr{N}_\infty }\left( {\mathit{\boldsymbol{F}},\mathit{\boldsymbol{r}}} \right) \le \exp \left( {{C_0}{r^{ - s}}} \right) $

其中:${\mathscr{N}}_\infty$(F, r)表示集合F半径为r球的覆盖数。

下面分析并行/分布式机器学习模型的泛化误差。可将泛化误差分解为采样误差、假设误差和近似误差3部分，则有

$ \varepsilon \left( {{\mathit{\boldsymbol{f}}_B}} \right) - \varepsilon \left( {{\mathit{\boldsymbol{f}}^ * }} \right) = \underbrace {{\varepsilon _S}\left( \mathit{\boldsymbol{f}} \right) - \varepsilon \left( \mathit{\boldsymbol{f}} \right) + \varepsilon \left( {{\mathit{\boldsymbol{f}}_B}} \right) - {\varepsilon _S}\left( {{\mathit{\boldsymbol{f}}_B}} \right)}_{采样误差} + \underbrace {{\varepsilon _S}\left( {{\mathit{\boldsymbol{f}}_B}} \right) - {\varepsilon _S}\left( \mathit{\boldsymbol{f}} \right)}_{假设误差} + \underbrace {\varepsilon \left( \mathit{\boldsymbol{f}} \right) - \varepsilon \left( {{\mathit{\boldsymbol{f}}^ * }} \right)}_{近似误差} $

其中:f^*∈C(X), f∈${\mathscr{H}}_K$是在样本S上学习的结果, f_B∈${\mathscr{H}}_K$是把样本分成B块后学习的结果, ε(·)为期望误差, ε_S(·)为经验误差。令样本规模为N, 基于以上假设和分析可给出如下泛化误差分析结果。

引理1^[16]  假设3—5成立, M′=max{2M, ‖f-f^*‖_∞}。对任意0 < δ < 1, 有

$ \Pr \left\{ {{\varepsilon _S}\left( \mathit{\boldsymbol{f}} \right) - \varepsilon \left( \mathit{\boldsymbol{f}} \right) + \varepsilon \left( {{\mathit{\boldsymbol{f}}_B}} \right) - {\varepsilon _S}\left( {{\mathit{\boldsymbol{f}}_B}} \right) \le 6M'L\left( {\frac{{{G_1}\left( {N/B,\delta } \right)}}{{N/B}} + \frac{{{G_2}\left( {N/B,\delta } \right)}}{{\sqrt {N/B} }}} \right) + \frac{1}{{{{\left( {N/B} \right)}^\tau }}}} \right\} \\ \ge 1 - \delta $

(3)

式中：τ=1/(s+2);P(N, δ)=C₀(8LMN^τ)^s-logδ; G₁(N, δ)=P(N, δ/2)+log(2/δ); G₂(N, δ)=$\sqrt {P\left( {N, \delta /2} \right)} + \sqrt {\log \left( {2/\delta } \right)} $。

引理2^[16]  假设3—5成立, 对任意0 < δ < 1, 有

$ \Pr \left\{ {{\varepsilon _S}\left( {{\mathit{\boldsymbol{f}}_B}} \right) - {\varepsilon _S}\left( \mathit{\boldsymbol{f}} \right) \le 6LM'\left( {\frac{{{G_1}\left( {N/B,\delta /2} \right)}}{{N/B}} + \frac{{{G_2}\left( {N/B,\delta /2} \right)}}{{\sqrt {N/B} }}} \right) + \frac{1}{{{{\left( {N/B} \right)}^\tau }}} + 2\lambda \left\| \mathit{\boldsymbol{f}} \right\|_2^2} \right\} \\ \ge 1 - \delta $

(4)

式中M′, G₁和G₂定义同引理1。

定理1  假设3—5成立, 当N足够大时, 对任意0 < δ < 1, f∈${\mathscr{H}}_K$, 有

$ \Pr \left\{ {\varepsilon \left( {{\mathit{\boldsymbol{f}}_B}} \right) - \varepsilon \left( {{\mathit{\boldsymbol{f}}^ * }} \right) \le 24LM\left( {\frac{{{G_1}\left( {N/B,\delta /4} \right)}}{{N/B}} + \frac{{{G_2}\left( {N/B,\delta /4} \right)}}{{\sqrt {N/B} }}} \right) + \frac{{2 + L}}{{{{\left( {N/B} \right)}^\tau }}} + 2\lambda \left\| \mathit{\boldsymbol{f}} \right\|_2^2} \right\} \\ \ge 1 - \delta $

(5)

式中:‖f-f^*‖_∞≤1/N, G₁和G₂定义同引理1。

证明  由假设3和假设5成立可知, 对任意N≥1, 存在f∈${\mathscr{H}}_K$, 有

$ {\left\| {\mathit{\boldsymbol{f}} - {\mathit{\boldsymbol{f}}^ * }} \right\|_\infty } < 1/N $

由假设4成立, 损失函数l(·)是L-Lipschiz连续的，有

$ \varepsilon \left( \mathit{\boldsymbol{f}} \right) - \varepsilon \left( {{\mathit{\boldsymbol{f}}^ * }} \right) = {\mathit{\boldsymbol{E}}_z}\left[ {l\left( {\mathit{\boldsymbol{f}},z} \right) - l\left( {{\mathit{\boldsymbol{f}}^ * },z} \right)} \right] \le L{\left\| {\mathit{\boldsymbol{f}} - {\mathit{\boldsymbol{f}}^ * }} \right\|_\infty } < L/N \le L/{\left( {L/B} \right)^\tau } $

(6)

所以, 近似误差上界为L/(N/B)^τ。当N足够大时, ‖f-f^*‖_∞ < 1/N→0。那么

$ M' = \max \left( {2M,{{\left\| {\mathit{\boldsymbol{f}} - {\mathit{\boldsymbol{f}}^ * }} \right\|}_\infty }} \right) = 2M $

(7)

将式(7)分别代入采样误差式(3)和假设误差式(4)并与近似误差式(6)求和, 可得式(5)。

定理1表明, 分块模型泛化误差界为O((N/B)^-τ)。分块数B越少, 每个进程上数据规模N/B越大, 分块模型泛化误差越小, 但每个进程的计算时间越长。所以, 选择最优分块数${\hat B}$, 可在保证并行/分布式机器学习模型泛化性的同时提高计算效率。

3 数据分块数选择准则

给定训练数据A={r_i=(x_i, y_i), i=1, 2, …, N}, 其中, x_i∈R^d, d为训练数据维度, N为训练集规模。

由经验风险最小化^[17]可得

$ \mathit{\boldsymbol{f}} = \mathop {\arg \min }\limits_{f \in {\mathscr{H}_K}} \frac{1}{N}\sum\limits_{i = 1}^N {l\left( {f,{\mathit{\boldsymbol{r}}_i}} \right)} $

其中:f为再生核希尔伯特空间${\mathscr{H}}_K$中的任意假设, l(·)为非负凸损失函数。

对训练数据A按行划分为B块^[18], 每个子数据块A_i∈R^|B_i|×d, 其中, |B_i|为子数据块规模, 且$\sum\limits_{i = 1}^B {\left| {{B_i}} \right| = N} $。

定义分块经验风险最小化, 可得

$ {f_B} = \mathop {\arg \min }\limits_{f \in {\mathscr{H}_K}} \frac{1}{N}\sum\limits_{i = 1}^B {{l_i}\left( {f,{\mathit{\boldsymbol{A}}_i}} \right)} $

其中l_i(·)为第i个子数据块的平均经验风险。

并行算法效率^[19]定义为

$ E = \frac{{{T_{\rm{s}}}}}{{{T_{\rm{p}}}B}} $

其中:T_s为串行时间, T_p为并行时间, B为进程数。

为了权衡模型的泛化性和并行效率, 提出并行效率敏感的数据分块数选择准则

$ \hat B = \mathop {\arg \min }\limits_{B \in \mathscr{B}} \sum\limits_{i = 1}^B {{l_i}\left( {{f_B},{\mathit{\boldsymbol{A}}_i}} \right)} + \eta E\left( B \right) $

其中:$\mathscr{B}$为分块数备选集, η为惩罚系数, δ≤E(B) < 1, δ为并行效率下界。

4 大规模支持向量机

本节采用所提出的数据分块数选择准则来构造一个大规模支持向量机模型。

在并行/分布式ADMM框架下的随机傅里叶特征空间中实现大规模支持向量机模型。给定标签数据集S={(x₁, y₁), (x₂, y₂), …, (x_N, y_N)}∈(X×Y)^N, 其中, X表示输入域, Y为输出域, x_i∈R^d, 标签y_i∈{-1, +1}, N为训练集规模。

由随机傅里叶特征映射式(2), 得到随机特征映射矩阵Z∈R^N×D, D为随机特征维度。将Z按行随机划分为B块^[18], 每个分块的样本规模为|B_j|。随机傅里叶特征映射显式地构造随机特征空间, 可在该随机特征空间中应用线性SVM来一致逼近高斯核SVM^[7]。

损失函数max(1-y_iω^Tz_i, 0)²是L-Lipschiz连续的^[20]。由分块经验风险最小化, 可得

$ {\mathit{\boldsymbol{\omega }}_B} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{\omega }}_j}} \sum\limits_{j = 1}^B {\sum\limits_{i \in {B_j}} {\max {{\left( {1 - {y_i}\mathit{\boldsymbol{\omega }}_j^{\rm{T}}{\mathit{\boldsymbol{z}}_i},0} \right)}^2}} } $

此时, D-ADMM中g(·)为指示函数^[21]。定义为

$ {{\tilde g}_S}\left( x \right) = \left\{ {\begin{array}{*{20}{c}} \begin{array}{l} 0\\ \infty \end{array}&\begin{array}{l} x \in S\\ x \notin S \end{array} \end{array}} \right. $

则υ^k+1:=Π_S(ω^k+1+u^k), 其中Π_S表示在封闭凸集S上的投影。

大规模SVM最优分块数选择为

$ \hat B = \mathop {\arg \min }\limits_{B \in \mathscr{B}} \sum\limits_{j = 1}^B {\sum\limits_{i \in {B_j}} {\max {{\left( {1 - {y_i}\mathit{\boldsymbol{\omega }}_B^{\rm{T}}{\mathit{\boldsymbol{z}}_i},0} \right)}^2} + \eta E\left( B \right)} } $

ADMM框架下随机傅里叶特征空间中数据分块数选择过程见算法2。

算法2  分块数选择算法(SNC)

输入：随机特征矩阵Z∈R^N×D, 分块数备选集B, 且|B|=t, 惩罚系数η, 并行效率下界δ。

(1) 初始化: E(B)=1;

(2) for k=1, 2, …, t do

(3) 调用D-ADMM计算ω_B=argmin_ωj$\sum\limits_{i = 1}^B {\sum\limits_{i \in {B_j}} {\max {{\left( {1 - {y_i}\mathit{\boldsymbol{\omega }}_j^{\rm{T}}{\mathit{\boldsymbol{z}}_i}, 0} \right)}^2}} } \;$;

(4) 更新E(B);

(5) 计算${V_k} = \sum\limits_{i = 1}^B {\sum\limits_{i \in {B_j}} {\max {{\left( {1 - {y_i}\mathit{\boldsymbol{\omega }}_B^{\rm{T}}{\mathit{\boldsymbol{z}}_i}, 0} \right)}^2}} } + \eta E\left( B \right)$;

(6) end for

(7) ${\hat B}$=argmin_B∈BV_k。

输出：最优分块数${\hat B}$。

对D-ADMM中的并行子问题利用对偶坐标下降算法^{[10, 22]}求解。要得到ε精确解, 迭代次数为O(log(1/ε)), 时间复杂度为O(nDlog(1/ε)), 其中, n为子数据块数据规模。算法SNC的迭代次数为t, 所以总的时间复杂度为O(tnDlog(1/ε))。

损失函数max(1-y_iω^Tz_i, 0)²和正则化函数1/2‖ω‖₂²均为封闭、适定凸函数, 约束条件为仿射函数。根据Slater条件, 对偶间隙为0, 强对偶性成立。故应用D-ADMM来并行/分布式求解大规模SVM满足收敛条件。

D-ADMM框架下大规模SVM问题为

$ \mathop {\min }\limits_{{\mathit{\boldsymbol{\omega }}_1}, \cdots ,{\mathit{\boldsymbol{\omega }}_{\hat B}},o} C\sum\limits_{j = 1}^{\hat B} {\sum\limits_{i \in {{\hat B}_j}} {\max {{\left( {1 - {y_i}\mathit{\boldsymbol{\omega }}_j^{\rm{T}}{\mathit{\boldsymbol{z}}_i},0} \right)}^2}} } + \frac{1}{2}\left\| \mathit{\boldsymbol{o}} \right\|_2^2,\;\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;\;\;{\mathit{\boldsymbol{\omega }}_j} - \mathit{\boldsymbol{o}} = \mathit{\boldsymbol{0}} $

其中:C为超参数, o为全局变量, ω_j是与第j个进程的局部变量。由D-ADMM可得

$ \mathit{\boldsymbol{\omega }}_j^{k + 1} = \mathop {\arg \min }\limits_{{\mathit{\boldsymbol{\omega }}_j}} C\sum\limits_{i \in {{\hat B}_j}} {\max {{\left( {1 - {y_i}\mathit{\boldsymbol{\omega }}_j^{\rm{T}}{\mathit{\boldsymbol{z}}_i},0} \right)}^2}} + \frac{\rho }{2}\left\| {{\mathit{\boldsymbol{\omega }}_j} - {\mathit{\boldsymbol{o}}^k} + \mathit{\boldsymbol{u}}_j^k} \right\|_2^2 $

$ {\mathit{\boldsymbol{o}}^{k + 1}} = \frac{{\sum\limits_{j = 1}^{\hat B} {\left( {\mathit{\boldsymbol{\omega }}_j^{k + 1} + \mathit{\boldsymbol{u}}_j^k} \right)} }}{{\hat B + 1/\rho }} $

$ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{u}}_j^{k + 1} = \mathit{\boldsymbol{u}}_j^k + \mathit{\boldsymbol{\omega }}_j^{k + 1} - {\mathit{\boldsymbol{o}}^{k + 1}}}&{j = 1, \cdots ,\hat B} \end{array} $

每个进程j处理一个子问题, 各个并行子问题利用对偶坐标下降算法求解ω_j^[22]。

5 实验结果及分析

本节实现并行/分布式ADMM框架下随机傅里叶特征空间中的大规模SVM, 并实验验证所提出的数据分块数选择准则。实验中使用6个标准数据集, 如表 1所示, 其中, 大规模SVM的超参数C和高斯核参数γ通过在11×11空间内进行格搜索的5-折交叉验证来选取, (C, γ)∈{2^-9，2 ^-7，…，2⁷，2⁹}。η为惩罚系数, 并行效率下界δ设为0.25, D-ADMM中惩罚系数ρ设为1, 绝对误差ε^abs和相对误差ε^rel均设为10^-4, ε设为10^-3。实验环境:曙光“星云”高性能计算集群。采用OpenMPI 1.4.5和C++实现并行算法。普通队列最多申请4节点, 每个节点32个核, 每个核分配内存2 GB, 主频2.2 GHz, 操作系统CentOS 5.8, 作业管理系统Torque 4.1.5。

对比实验结果如表 2所示。其中, Acc表示测试精度, 计算时间和测试精度为重复10次实验的平均值。

实验结果表明, 最优分块数相比于其他分块数下的并行模型预测精度相当, 但计算时间大幅缩减。如在webspam数据集上, 在最优分块数为12, 相比于B=2而言, 计算时间大幅缩短。

分块数过多, 单节点任务规模太小, 将会导致额外开销(如负载不均衡、进程间通信)增大, 总时间反而会增加。如在covtype数据集上, 在最优分块数为${\hat B}$=8下模型分类精度高于B=14, 同时计算时间更短; 同样, 在其他数据集上也可得出类似的结论。

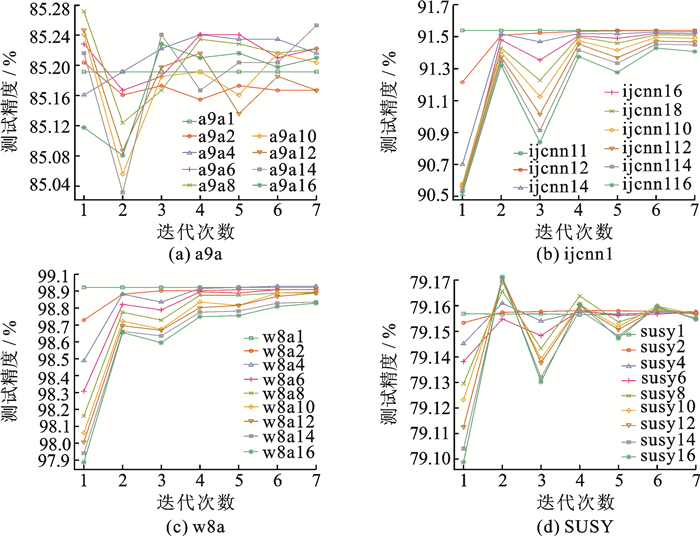
为了验证不同分块数对模型测试精度的影响, 给出测试精度随着迭代次数的变化曲线, 如图 1所示。

结果表明, 在相同迭代次数下, 随着分块数的增多, 模型的测试精度逐渐下降。这与第2节的泛化误差分析结果一致。

6 结束语

现有并行/分布式机器学习方法缺少有理论依据的数据分块数选择准则。针对这一问题, 推导并行/分布式机器学习模型的泛化误差与分块数目的关系, 折衷泛化性与并行效率, 进而提出一个并行效率敏感的并行/分布式机器学习数据分块数选择准则。大规模支持向量机的理论分析和实验结果表明, 所提出的数据分块数选择准则, 可保证测试精度并提高计算效率。虽然所提出的数据分块数选择准则适用于ADMM框架下随机傅里叶特征空间中的大规模支持向量机, 该数据分块数准则及分析方法也适用于其他并行/分布式机器学习模型, 如大规模核岭回归等。