引言

信号波达方向(Direction of arrival，DOA)估计是阵列信号处理领域研究的主要问题之一^[1]。电磁矢量传感阵列可同时获取信号的DOA信息和极化信息，而传统标量传感器阵由于所有阵元的极化方式相同，只能接收电磁信号的某一分量，其阵列输出仅反映信号强度的复幅度，无法检测信号的极化信息。与标量阵列相比，电磁矢量传感阵列具有较强的抗干扰能力、稳健的检测能力、较高的系统分辨能力和极化多址能力，为阵列性能的进一步改善提供了物理基础^[2]。文献[3, 4]将标量传感器阵列中的借助旋转不变技术的信号参数估计方法(Estimation of signal parameters via rotational invariance technique, ESPRIT)推广到电磁矢量传感器阵列，其中文献[3]在正交偶极子构成均匀线阵中利用阵列两方面的旋转不变特性，实现了一维角度和极化参数的联合估计。文献[4]将线阵算法推广到均匀矩形面阵，实现了电磁矢量均匀面阵中的二维角度和极化参数的估计。文献[5]通过构造拉格朗日代价函数，对电磁矢量均匀线阵的多重信号分类(Multiple signal classification, MUSIC)空间谱函数进行降维，算法可以适应不规则的阵列结构。文献[6]针对电磁矢量传感器多输入多输出(Multiple-input multiple-output, MIMO)雷达，将传统MUSIC算法的四维谱峰搜索降至一维搜索，用极低的复杂度实现了离开角(Direction of Departure, DOD), DOA和极化联合估计。文献[7]提出的DOA和极化联合估计算法，适用于阵列阵元间距大于入射信号半波长的情况，有效扩展了阵列孔径。

但在传统电磁矢量阵的参数估计算法中，阵列布阵往往为满阵，相邻阵元的间距必须满足d≤λ/2，其中λ为入射信号波长。而满阵存在相邻阵元互耦严重、阵列孔径小、分辨率差和测向精度低等不足，无法满足实际环境需求。在这种背景下稀疏阵列被提出并开始推广应用。稀疏阵列^[8-16]是指相邻阵元以间距大于半波长均匀或非均匀稀疏排布的一种阵列。稀疏阵列相比传统满阵具有更多优势，如相同阵元数时能够有效扩展阵列孔径，减小了阵元的互耦效应，改善了DOA估计的测向精度和分辨率等。

互质阵列是稀疏阵列的一种重要形式，由两个阵元数和阵元间距存在互质关系的均匀子阵穿插拓扑构成，通过子阵的互质关系可以有效消除测向模糊。与阵元数相等的均匀线阵相比，互质阵列具有更大的阵列孔径，在DOA估计中具有相对更高的自由度^[11]，正成为稀疏阵列中一个热门研究方向。文献[16]最早提出互质线阵的概念，证明了M+N－1个阵元的互质线阵可获得O(MN)的自由度。文献[17]在互质阵列的互质特性基础上，提出了互质阵中的联合MUSIC估计算法。文献[18]提出了一种互质面阵，将均匀面阵中的传统二维MUSIC算法推广到该阵列，并进一步提出局部谱峰搜索算法，实现了较低复杂度的二维参数估计。文献[19, 20]通过互质稀疏子阵结构的优化组合，实现了无自由度性能损失的DOA估计。文献[21]利用和阵列与差阵列，得到一个大于实际阵列的虚拟阵列，引入稀疏恢复方法，大大扩展了自由度与阵列孔径。文献[22]提出了一种离网型(off-grid)的互质阵列波达方向估计算法。目前将互质阵列与电磁矢量传感器阵列相结合的研究相对还比较少，文献[23]主要利用平滑的极化多重信号分类法进行电磁矢量互质面阵中的参数估计，文献[24]在假设极化信息已知的条件下，研究了电磁矢量互质阵中由传统MUSIC算法改进的综合极化信息的MUSIC算法。

本文将传统电磁矢量均匀阵列推广为电磁矢量互质阵列，突破了阵元间距不大于半波长的限制，提出了电磁矢量互质阵列中基于降维Capon的DOA和极化联合估计算法，无需假设极化信息已知，且参数估计只需一维搜索，避免了多维搜索。阵元数相同时，与电磁矢量均匀线阵中的估计性能相比，本文阵列明显提高了降维Capon的角度估计性能，并拓展了天线孔径，具有相对较高的自由度，且降低了运算复杂度。同时，在相同阵列条件下，本文算法的角度估计性能优于ESPRIT算法和三线性分解算法。

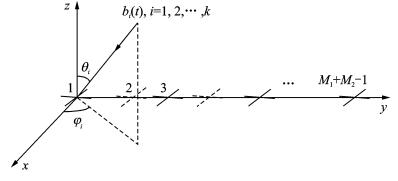
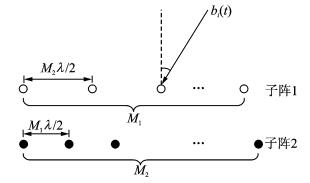
1 数据模型

考虑如图 1所示的电磁矢量互质线阵，该阵列由M₁+M₂－1个正交偶极子对稀疏排布构成。互质线阵具体拓扑结构如图 2，由两个均匀子阵构成，记作子阵1和子阵2，其中，每个阵元由一对分别平行于x轴和y轴方向的正交偶极子构成，各阵元沿y轴正半轴排列，子阵1和子阵2的阵元数分别为M₁和M₂，阵元间距分别为d₁=M₂λ/2和d₂=M₁λ/2，M₁和M₂互为质数，λ为波长。子阵1和子阵2只在原点处有一个阵元重合。假设有K个远场独立信号入射到该阵列，每个信号到达角均不同，第k个信号的到达角记作$ {\theta _k}\left( {k = 1, 2, \ldots , K} \right)$，对应的极化参数为$ \left( {{\gamma _k}, {\eta _k}} \right)$。

双极化敏感阵元接收到的第k个信源的电压为^[2]

$ {\mathit{\boldsymbol{r}}_k}\left( t \right) = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _k}\cos {\varphi _k}}&{ - \sin {\varphi _k}}\\ {\cos {\theta _k}\sin {\varphi _k}}&{\cos {\varphi _k}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\sin {\gamma _k}{{\rm{e}}^{{\rm{j}}{\eta _k}}}}\\ {\cos {\gamma _k}} \end{array}} \right]{\mathit{\boldsymbol{b}}_k}\left( t \right) = {\mathit{\boldsymbol{s}}_k}{\mathit{\boldsymbol{b}}_k}\left( t \right) $

(1)

其中，s_k∈C^2×1为接收极化矢量，其表达式为

$ {\mathit{\boldsymbol{s}}_k} = \left[ {\begin{array}{*{20}{c}} {\cos {\theta _k}\cos {\varphi _k}}&{ - \sin {\varphi _k}}\\ {\cos {\theta _k}\sin {\varphi _k}}&{\cos {\varphi _k}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\sin {\gamma _k}{{\rm{e}}^{{\rm{j}}{\eta _k}}}}\\ {\cos {\gamma _k}} \end{array}} \right] $

(2)

将电磁矢量互质线阵分成子阵1和子阵2来单独分析阵列信号接收模型。分析子阵时，相当于分析电磁矢量均匀线阵中的信号接收模型，此时方位角φ_k=90° (k=1, 2, …, K)。在M个阵元的均匀线阵中，记原点的阵元为参考阵元，相邻阵元间距为d，第m个阵元相对参考阵元的相位滞后为$ - 2{\rm{ \mathit{ π} }}\left( {m - 1} \right)d{\rm{sin}}\theta /\lambda $。故对于K个入射信号、J个快拍的情况，不考虑噪声的条件下，第i个子阵(i=1, 2)的接收信号可表示为^[25]

$ {\mathit{\boldsymbol{X}}_i} = \left[ {{\mathit{\boldsymbol{a}}_{i1}} \otimes {\mathit{\boldsymbol{s}}_1},{\mathit{\boldsymbol{a}}_{i2}} \otimes {\mathit{\boldsymbol{s}}_2}, \cdots ,{\mathit{\boldsymbol{a}}_{iK}} \otimes {\mathit{\boldsymbol{s}}_K}} \right]{\mathit{\boldsymbol{B}}^{\rm{T}}} = \left( {{\mathit{\boldsymbol{A}}_i} \odot \mathit{\boldsymbol{S}}} \right){\mathit{\boldsymbol{B}}^{\bf{T}}} $

(3)

式中：${\mathit{\boldsymbol{a}}_{ik}} = {\rm{ }}{[1, {{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathit{ π} }}{d_i}{\rm{sin}}{\theta _k}/\lambda }}, \ldots , {{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathit{ π} }}{d_i}({M_i} - 1){\rm{sin}}\theta {_k}/\lambda }}{\rm{ }}]^{\rm{T}}} $为第i个子阵接收的第k个信源的导向矢量，s_k为第k个信源的极化矢量, $ \mathit{\boldsymbol{B}} = {\rm{ }}[{\mathit{\boldsymbol{b}}_1}, {\mathit{\boldsymbol{b}}_2}, \ldots {\rm{ }}, {\mathit{\boldsymbol{b}}_K}] \in {\mathit{\boldsymbol{C}}^{J \times K}}$为信源矩阵，b_k为入射到阵列的第k个信源，$ {\mathit{\boldsymbol{A}}_i} = \left[ {{\mathit{\boldsymbol{a}}_{i1}}, {\mathit{\boldsymbol{a}}_{i2}}, {\rm{ }} \ldots , {\mathit{\boldsymbol{a}}_{iK}}} \right] $为第i个子阵的方向矩阵，$\mathit{\boldsymbol{S}} = {\rm{ }}[{\mathit{\boldsymbol{s}}_1}, {\mathit{\boldsymbol{s}}_2}, {\rm{ }} \ldots , {\mathit{\boldsymbol{s}}_K}]$为极化矩阵，$ \otimes $和⊙分别为Kronecker积和Khatri-Rao积。

对于图 1的信号模型，第i个子阵(i=1, 2)通过获取J个快拍得到协方差矩阵R_ix的估计为

$ {{\mathit{\boldsymbol{\hat R}}}_{ix}} = \frac{1}{J}\sum\limits_j^J {{\mathit{\boldsymbol{x}}_i}\left( {{\mathit{\boldsymbol{t}}_j}} \right)\mathit{\boldsymbol{x}}_i^{\rm{H}}\left( {{\mathit{\boldsymbol{t}}_j}} \right)} $

(4)

2 DOA和极化估计算法

根据电磁矢量互质线阵的两个子阵都是均匀线阵，且同一种阵列分析方法相同，故本文首先分别在子阵1和子阵2的基础上进行参数估计。但电磁矢量均匀线阵条件下的传统Capon算法需进行三维谱峰搜索，运算复杂度过高。因此本文通过降维处理，只需在两个子阵中分别进行一维谱峰搜索即可实现参数估计，复杂度得到降低，后利用两个子阵的互质特性解模糊得出真实角度估计，最后进一步得出与真实角度匹配的极化参数估计。

2.1 3D-Capon算法

Capon算法将阵列中可控的自由度用来形成期望的波束形状，达到对有用信号进行提升和对无用信号进行抑制，第i个子阵(i=1, 2)的多维Capon谱函数可通过类比一维Capon算法得到^[26]

$ {P_{{\rm{iMD - Capon}}}}\left( {\theta ,\gamma ,\eta } \right) = \frac{1}{{{{\left[ {{\mathit{\boldsymbol{a}}_i}\left( \theta \right) \otimes \mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right)} \right]}^{\rm{H}}}\mathit{\boldsymbol{\hat R}}_{ix}^{ - 1}\left[ {{\mathit{\boldsymbol{a}}_i}\left( \theta \right) \otimes \mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right)} \right]}} $

(5)

其中, ${{\mathit{\boldsymbol{\hat R}}}_{ix}} $根据式(4)构造得到。

$ {\mathit{\boldsymbol{a}}_i}\left( \theta \right) = {\left[ {1,{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{d_i}\sin \theta /\lambda }},{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{d_i} \times 2\sin \theta /\lambda }}, \cdots ,{{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathsf{ π} }}{d_i}\left( {{M_i} - 1} \right)\sin \theta /\lambda }}} \right]^{\rm{T}}} $

(6)

$ \mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) = {\left[ { - \cos \gamma ,\cos \theta \sin \gamma {{\rm{e}}^{{\rm{j}}\eta }}} \right]^{\rm{T}}} $

(7)

当不存在角度模糊时，在各子阵中搜索θ，γ和η，式(5)的K个较大的峰值对应θ，γ和η即为待估计的DOA和极化参数。由于存在角度模糊，因此各子阵通过三维搜索得到式(5)所有峰值对应的θ中包含真实角度和模糊角度，角度模糊需利用解模糊方法消除。但三维搜索复杂度过高，故先用降维方法降低搜索维数。

2.2 降维Capon算法

分析子阵1时，定义$ {\mathit{\boldsymbol{V}}_1}\left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right), \mathit{\boldsymbol{s}}\left( {{\rm{ }}\theta , \gamma , \eta } \right)} \right]{\rm{ }} = \left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right) \otimes \mathit{\boldsymbol{s}}\left( {\theta , \gamma , \eta } \right)} \right]{^{\rm{H}}}\mathit{\boldsymbol{\hat R}}_{1x}^{ - 1}\left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right) \otimes \mathit{\boldsymbol{s}}\left( {\theta , \gamma , \eta } \right)} \right]$，该式也可表示为

$ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_1}\left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right),\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right)} \right] = {\mathit{\boldsymbol{s}}^{\rm{H}}}\left( {\theta ,\gamma ,\eta } \right){{\left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right) \otimes {\mathit{\boldsymbol{I}}_2}} \right]}^{\rm{H}}}\mathit{\boldsymbol{\hat R}}_{1x}^{ - 1}\left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right) \otimes {\mathit{\boldsymbol{I}}_2}} \right]\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) = }\\ {{\mathit{\boldsymbol{s}}^{\rm{H}}}\left( {\theta ,\gamma ,\eta } \right){\mathit{\boldsymbol{Q}}_1}\left( \theta \right)\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right)} \end{array} $

(8)

其中，$ {\mathit{\boldsymbol{Q}}_1}\left( \theta \right){\rm{ }} = {\left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right) \otimes {\mathit{\boldsymbol{I}}_2}} \right]^{\rm{H}}}\mathit{\boldsymbol{\hat R}}_{1x}^{ - 1}\left[ {{\mathit{\boldsymbol{a}}_1}\left( \theta \right) \otimes {\mathit{\boldsymbol{I}}_2}} \right] \in {{\bf{C}}^{2 \times 2}}, {\mathit{\boldsymbol{I}}_2} \in {{\bf{C}}^{2 \times 2}}$为单位矩阵。式(8)是一个二次优化问题，用约束条件${\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{s}}\left( {\theta , \gamma , {\rm{ }}\eta } \right) = 1 $来消除该方程$\mathit{\boldsymbol{s}}\left( {\theta , \gamma , \eta } \right) = \mathit{\boldsymbol{0}} $的平凡解，其中$\mathit{\boldsymbol{e}} = {\left[ {1, 0} \right]^{\rm{T}}} \in {{\bf{R}}^{2 \times 1}} $。因此这个二次优化问题可重新构建为下列形式的线性约束最小方差问题^[5]，即

$ \mathop {\min }\limits_{\theta ,\gamma ,\eta } {\mathit{\boldsymbol{s}}^{\rm{H}}}\left( {\theta ,\gamma ,\eta } \right){\mathit{\boldsymbol{Q}}_1}\left( \theta \right)\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right)\;\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;\;{\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) = 1 $

(9)

构造如下代价函数

$ L\left( {\theta ,\gamma ,\eta } \right) = {\mathit{\boldsymbol{s}}^{\rm{H}}}\left( {\theta ,\gamma ,\eta } \right){\mathit{\boldsymbol{Q}}_1}\left( \theta \right)\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) - {\lambda _1}\left( {{\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) - 1} \right) $

(10)

其中λ₁是常数，对s(θ, γ, η)求导有

$ \frac{\partial }{{\partial \mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right)}}L\left( {\theta ,\gamma ,\eta } \right) = 2{\mathit{\boldsymbol{Q}}_1}\left( \theta \right)\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) + {\lambda _1}\mathit{\boldsymbol{e}} = 0 $

(11)

根据式(11)得, $\mathit{\boldsymbol{s}}\left( {\theta , \gamma , \eta } \right) = \mu \mathit{\boldsymbol{Q}}_1^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}} $，其中μ是常数。由${\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{s}}\left( {\theta , \gamma , {\rm{ }}\eta } \right) = 1, \mu = 1/{e^{\rm{H}}}\mathit{\boldsymbol{Q}}_1^{ - 1}\left( \theta \right){\rm{ }}\mathit{\boldsymbol{e}} $，得到$\mathit{\boldsymbol{s}}\left( {\theta , \gamma , {\rm{ }}\eta } \right) $为

$ \mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) = \frac{{\mathit{\boldsymbol{Q}}_1^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}}}{{{\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{Q}}_1^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}}} $

(12)

将式(12)代入式(9)，可以得到

$ {{\hat \theta }_{1k}} = \mathop {\arg \min }\limits_\theta \frac{1}{{{\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{Q}}_1^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}}} = \mathop {\arg \max }\limits_\theta {\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{Q}}_1^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}\;\;\;\;\;\;\;k = 1,2, \cdots ,K $

(13)

记$ {{\hat u}_{1k}} = {\rm{sin}}({{\hat \theta }_{1k}})$，可通过在区间u∈[－1, +1]对u_1k进行全局搜索，寻找矩阵Q₁^-1(θ)的(1, 1)元素的所有峰值，这些峰值对应的角度即为子阵1的所有模糊角度估计信息。

同理，分析子阵2时，定义${\mathit{\boldsymbol{V}}_2}\left[ {{\mathit{\boldsymbol{a}}_2}\left( \theta \right), \mathit{\boldsymbol{s}}\left( {\theta , \gamma , \eta } \right)} \right]{\rm{ }} = \left[ {{\mathit{\boldsymbol{a}}_2}\left( \theta \right) \otimes \mathit{\boldsymbol{s}}\left( {\theta , \gamma , \eta } \right)} \right]{^{\rm{H}}}\mathit{\boldsymbol{\hat R}}_{2x}^{ - 1}\left[ {{\mathit{\boldsymbol{a}}_2}\left( \theta \right) \otimes \mathit{\boldsymbol{s}}\left( {\theta , \gamma , \eta } \right){\rm{ }}} \right] $，令${\mathit{\boldsymbol{Q}}_2}\left( \theta \right) = {\left[ {{\mathit{\boldsymbol{a}}_2}\left( \theta \right) \otimes {\mathit{\boldsymbol{I}}_2}} \right]^{\rm{H}}}\mathit{\boldsymbol{\hat R}}_{2x}^{ - 1}\left[ {{\mathit{\boldsymbol{a}}_2}\left( \theta \right) \otimes {\mathit{\boldsymbol{I}}_2}} \right] \in {{\bf{C}}^{2 \times 2}} $，通过构建线性约束最小方差问题，即

$ \mathop {\min }\limits_{\theta ,\gamma ,\eta } {\mathit{\boldsymbol{s}}^{\rm{H}}}\left( {\theta ,\gamma ,\eta } \right){\mathit{\boldsymbol{Q}}_2}\left( \theta \right)\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right)\;\;\;\;{\rm{s}}.\;{\rm{t}}.\;\;\;\;{\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) = 1 $

(14)

进一步推导可得

$ \mathit{\boldsymbol{s}}\left( {\theta ,\gamma ,\eta } \right) = \frac{{\mathit{\boldsymbol{Q}}_2^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}}}{{{\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{Q}}_2^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}}} $

(15)

最后得到

$ {{\hat \theta }_{2k}} = \mathop {\arg \min }\limits_\theta \frac{1}{{{\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{Q}}_2^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}}} = \mathop {\arg \max }\limits_\theta {\mathit{\boldsymbol{e}}^{\rm{H}}}\mathit{\boldsymbol{Q}}_2^{ - 1}\left( \theta \right)\mathit{\boldsymbol{e}}\;\;\;\;\;\;\;k = 1,2, \cdots ,K $

(16)

同样地，记${{\hat u}_{2k}} = {\rm{sin}}({{\hat \theta }_{2k}}) $，可通过在区间u∈[－1, +1]对u_2k进行全局搜索，寻找矩阵Q₂^-1(θ)的(1, 1)元素的所有峰值，从而得到子阵2的所有模糊角度估计信息。

2.3 角度模糊消除

结合式(13, 16)以及角度模糊产生原理^[16]，可知电磁矢量互质线阵中角度模糊产生只与a_i(θ)有关。因此通过找到两个均匀子阵得到的相同角度值，即可消除角度模糊，证明如下：

当一个信源以θ₀入射到M个阵元的均匀线阵中，产生角度模糊时有

$ \mathit{\boldsymbol{a}}\left( {{\theta _0}} \right) = \mathit{\boldsymbol{a}}\left( {{{\theta '}_0}} \right)\;\;\;\;\;\;\;{\theta _0} \ne {{\theta '}_0} $

(17)

其中，θ₀和θ′₀分别为真实入射角和模糊角，$\mathit{\boldsymbol{a}}\left( \theta \right){\rm{ }} = {\left[ {1, {{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathit{ π} }}d{\rm{sin}}\theta /\lambda }}, \ldots , {{\rm{e}}^{ - {\rm{j}}2{\rm{ \mathit{ π} }}d\left( {M - 1} \right){\rm{sin}}\theta /\lambda }}} \right]^{\rm{T}}} $，d为相邻阵元间距。

考虑单个信源入射到互质线阵时，假设子阵1和子阵2存在两个相同的估计结果θ和θ′。对于子阵1，阵元间距为d₁=M₂λ/2，根据式(17)有

$ \sin \left( \theta \right) - \sin \left( {\theta '} \right) = 2{k_1}/{M_2} $

(18)

其中$ {k_1} = - ({M_2} - 1), \ldots , - 1, 1, \ldots , ({M_2} - 1)$。

同理，对于子阵2有

$ \sin \left( \theta \right) - \sin \left( {\theta '} \right) = 2{k_2}/{M_1} $

(19)

其中${k_1} = - ({M_2} - 1), \ldots , - 1, 1, \ldots , ({M_2} - 1) $。

结合式(18)和式(19)可以得到

$ \frac{{2{k_1}}}{{{M_2}}} = \frac{{2{k_2}}}{{{M_1}}} $

(20)

由于M₁, M₂互为质数，除k₁=k₂=0外，没有符合条件的k₁, k₂使式(20)成立。由此可以说明，互质线阵中两个子阵得到的相同角度估计值，即为真实的角度估计结果。因此通过对比子阵1和子阵2的所有模糊DOA估计信息，找到其中的相同角度值θ_k即为真实的DOA估计值。

2.4 极化估计

由于两个子阵接收极化矢量相同，结合式(12, 15)，根据所得的真实DOA估计值最终可以得到K个矢量$ \mathit{\boldsymbol{\hat s}}({\theta _1}, {\gamma _1}, {\eta _1}), \mathit{\boldsymbol{\hat s}}{\rm{ }}({\theta _2}, {\gamma _2}, {\eta _2}), \ldots , \mathit{\boldsymbol{\hat s}}({\theta _k}, {\gamma _k}, {\eta _k})$。在不考虑噪声的情况下，估计所得第k个信源的极化矢量可以表示为$\mathit{\boldsymbol{\hat s}}({\theta _k}, {\gamma _k}, {\eta _k}) = \left[ {1, - {\rm{cos}}{\theta _k}{\rm{tan}}{\gamma _k}{\rm{}}{{\rm{e}}^{{\rm{j}}{\eta _k}}}} \right]{^{\rm{T}}} $。

为简单表示，定义$ {{\mathit{\boldsymbol{\hat s}}}_k}\mathop \Delta \limits_ = \mathit{\boldsymbol{\hat s}}({\theta _k},{\gamma _k},{\eta _k})$，则极化参数估计为

$ \begin{array}{*{20}{c}} {{{\hat \eta }_k} = {\rm{angle}}\left( {{{\mathit{\boldsymbol{\hat s}}}_k}\left( 2 \right)} \right)}\\ {{{\hat \gamma }_k} = \arctan \left( {\frac{{{\rm{abs}}\left( {{{\mathit{\boldsymbol{\hat s}}}_k}\left( 2 \right)} \right)}}{{\cos {{\hat \theta }_k}}}} \right)} \end{array} $

(21)

式中：$ {{\mathit{\boldsymbol{\hat s}}}_k}$ (2)表示$ {{\mathit{\boldsymbol{\hat s}}}_k}$的第2个元素，angle(·)表示对复数阵各个元素取相角，abs(·)表示对复数阵各个元素取幅值。

2.5 算法主要步骤

上述推导已经给出了电磁矢量互质线阵中基于降维Capon的参数估计实现过程，算法主要步骤如下：

(1) 根据第i个子阵i(i=1, 2)接收信号构造协方差矩阵R_i，求逆得到R_i^－1。

(2) 通过一维全局搜索，找出Q_i^－1(θ)的(1, 1)元素的所有峰值，根据峰值对应的角度得到每个子阵的所有模糊DOA估计信息。

(3) 对比子阵1和子阵2的所有模糊DOA估计信息，找到其中的相同角度值θ_k即为真实的DOA估计值。

(4) 结合式(12, 15)得到$\mathit{\boldsymbol{\hat s}}({\theta _k}, {\gamma _k}, {\eta _k}) $，根据式(21)，求出极化参数γ_k和η_k的估计。

3 算法仿真结果与性能分析

通过Monte Carlo仿真中的求根均方误差(Root mean squares error, RMSE)评估算法性能，Monte Carlo仿真次数为1 000，定义角度求根均方误差RMSE_a，极化求根均方误差RMSE_γ和RMSE_η分别为

$ {\rm{RMS}}{{\rm{E}}_a} = \frac{1}{K}\sum\limits_{k = 1}^K {\sqrt {\frac{1}{{1\;000}}\sum\limits_{l = 1}^{1\;000} {\left[ {{{\left( {{{\hat \theta }_{k,l}} - {\theta _k}} \right)}^2}} \right]} } } $

(22)

$ {\rm{RMS}}{{\rm{E}}_\gamma } = \frac{1}{K}\sum\limits_{k = 1}^K {\sqrt {\frac{1}{{1\;000}}\sum\limits_{l = 1}^{1\;000} {\left[ {{{\left( {{{\hat \gamma }_{k,l}} - {\gamma _k}} \right)}^2}} \right]} } } $

(23)

$ {\rm{RMS}}{{\rm{E}}_\eta } = \frac{1}{K}\sum\limits_{k = 1}^K {\sqrt {\frac{1}{{1\;000}}\sum\limits_{l = 1}^{1\;000} {\left[ {{{\left( {{{\hat \eta }_{k,l}} - {\eta _k}} \right)}^2}} \right]} } } $

(24)

式中：${{\hat \theta }_{k, l}}, {{\hat \gamma }_{k, l}} $和$ {{\hat \eta }_{k, l}}$分别为第l次仿真时的θ_k, γ_k和η_k的估计值。仿真试验采用双极化天线构成的互质线阵。假设空域有K=2个信源，它们的角度和极化参数(θ, γ, η)分别为(10°, 7 °, 15°)和(20°, 17°, 25°)，M₁和M₂分别为子阵1和子阵2的阵元数，M为均匀线阵的阵元数，J为快拍数。

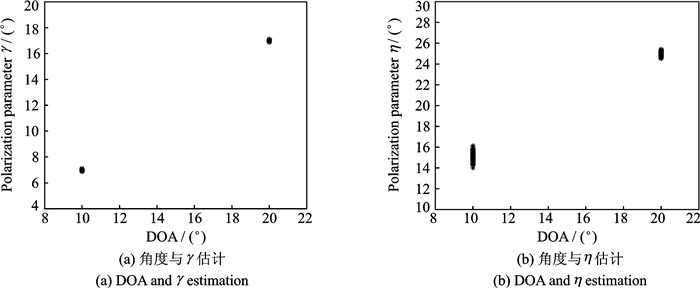
图 3为本文算法在信噪比SNR =25 dB条件下，仿真100次的角度和极化参数估计的散点图。仿真过程中，M₁=4, M₂ = 5, J=200。从图 3中可以看出，本文算法可以有效地估计出角度和极化参数，且角度和极化参数是有效配对的。

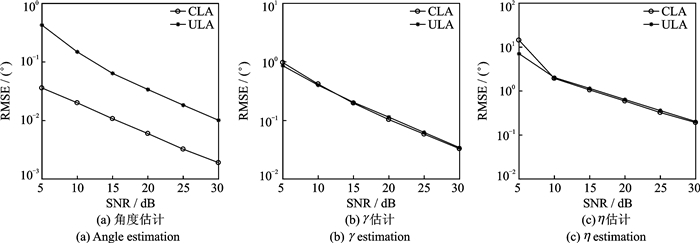
图 4为降维Capon算法在阵元数相同的互质线阵和均匀线阵中的性能对比。仿真过程中，M₁=4, M₂=5, M=8, J=200。其中，CLA表示互质线阵，ULA表示均匀线阵。由图 4可以看出，与阵元数相同的电磁矢量均匀线阵相比，电磁矢量互质线阵下的降维Capon算法具有更优越的DOA估计性能。

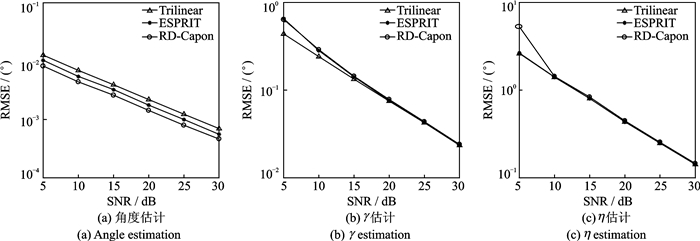
图 5为本文算法与相同阵列条件下的ESPRIT算法、三线性分解算法的性能对比。仿真过程中，M₁=7, M₂=9, J=200。从图 5中可以看出，相同阵列条件下，本文中降维Capon算法的DOA估计性能优于ESPRIT算法、三线性分解算法。

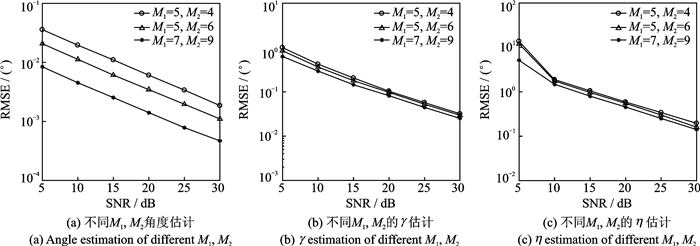
图 6为本文算法参数估计性能在不同阵元数下的仿真结果，仿真中快拍数J=200。从图 6可以看出，算法的DOA和极化参数估计性能都随着阵元数的增加而改善。

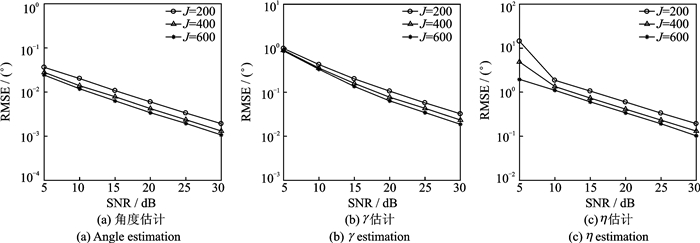
图 7为本文算法在不同快拍数下的仿真结果，仿真过程中M₁=4, M₂=5。从图 7中可知，算法的DOA和极化参数估计性能随着快拍数增加都变得更好。本文算法运算复杂度分析如下：设子阵1和子阵2的阵元数分别为M₁和M₂，信源数为K，快拍数为J，本文降维Capon算法的主要运算复杂度包括：计算R_i所需复杂度为$ O\{ 4J(M_1^2 + M_2^2)\} , {\mathit{\boldsymbol{R}}_i}$求逆所需复杂度为$O\{ 8(M_1^3 + M_2^3)\} $，计算Q(θ)需要复杂度为$ O\{ 8(M_1^2 + M_2^2 + {M_1} + {M_2})\} $，因此本文降维Capon算法的复杂度可以表示为$ O\{ 4J(M_1^2 + M_2^2) + 8(M_1^3 + M_2^3) + {n_1}[8(M_1^2 + M_2^2 + {M_1} + {M_2})]$, 其中n₁是一维全局搜索时的步数。设均匀线阵的阵元数为$M = {M_1} + {M_2} - 1 $，可得电磁矢量均匀线阵中降维Capon算法的运算复杂度为$O\{ 4JM + 8M{^3} + {n_2}[8{M^2} + 8M] $, 其中n₂是全局搜索时的步数。由此可见当阵元数相同时，电磁矢量互质线阵中算法复杂度更低。本文中降维Capon算法的优点：(1)本文算法只需要一维搜索，避免了传统Capon算法的三维谱峰搜索，算法复杂度大大降低; (2)本文算法中DOA和极化参数可自动配对; (3)阵元数相同时，与电磁矢量均匀线阵中的估计性能相比，该算法在互质线阵中具有更优越的DOA估计性能; (4)本文算法的角度估计性能优于ESPRIT算法、基于平行因子的三线性分解算法。

4 结束语

本文将互质阵空间谱算法与电磁矢量传感器阵列相结合，利用降维Capon算法解决了电磁矢量互质阵中DOA和极化联合估计问题。首先在子阵基础上进行参数估计，然后利用互质线阵解模糊方法得出真实角度估计，最后进一步得出与真实角度匹配的极化参数估计。本文算法将三维谱峰搜索降至一维搜索，大大降低了运算复杂度。仿真结果表明，与阵元数相同的均匀阵列中降维Capon算法相比，本文阵列中的算法具有更优越的角度估计性能，并拓展了天线孔径，且运算复杂度更低；相同阵列条件下，本文算法的角度估计性能优于ESPRIT算法和三线性分解算法。