2. 苏州大学机器学习与类脑计算国际合作联合实验室, 苏州, 215006
2. Joint International Research Laboratory of Machine Learning and Neuromorphic Computing, Soochow University, Suzhou, 215006, China
近年来,随着科学技术的发展,数据的数量和维度呈现出快速增长的趋势。降维不仅可以简化模型、降低模型的训练时间,而且可以提高模型的泛化能力。因为高维数据难以表达且需要较高的计算和存储代价,所以降维方法成为机器学习和模式识别领域中的热门研究方向,并已在人脸识别、手写体识别等系统中取得了良好的效果。
降维方法可分为线性和非线性两种。线性降维方法,如主成分分析法(Principal component analysis, PCA)[1]、线性判别分析(Linear discriminant analysis, LDA) [2]等,几何表达简单、计算成本较低,是分析高维数据的基础。PCA由Karl Pearson于1901年提出, 该方法使用正交线性变换将一组观测的可能相关变量转换为一组线性不相关变量,这些不相关变量叫做主成分。拥有最大方差,即尽可能不相关的数据称为第一主成分,并以此类推。PCA算法的核心是对数据协方差矩阵进行特征分解。LDA算法与方差分析和回归分析密切相关,它试图找到一组特征的线性组合,能将多个对象尽量分开,即找到最佳投影方向。
如果所需的特征在一个低维的流形子空间中,那么传统的线性降维算法并不能很好地提取出该非线性结构,因此很多非线性的流形学习算法被提出,包括等距映射(Isomap)[3]、拉普拉斯特征映射(Laplacian eigenmaps, LE)[4]及局部线性嵌入(Locally-linear embedding, LLE)[5]等。
但是以上流形学习算法只考虑了训练样本,处理过程中未能得到一个显式映射,因此不能处理新样本,即所谓的“out of sample”问题。针对这个问题,He等人提出了保局算法(Locality preserving projection, LPP)[6]和局部保持嵌入算法(Neighborhood preserving embedding, NPE) [7]:(1) LPP算法首先整合邻近点信息建立一个图,该图可看做一个连续流形结构的线性离散近似[6],然后使用拉普拉斯算子计算出转换矩阵将数据点映射到低维子空间; LPP算法使原始高维空间中距离相近点在降维后依旧保持近距离。(2) NPE算法的目的在于保持局部流形结构。在一定范围内给定一些数据点,首先建立权重矩阵来描述数据点之间的关系,并将每个点用邻近点线性表示; 然后找到一个最佳嵌入使得该邻近结构在低维空间中得以保持。以上两个利用局部信息进行降维的算法虽然没有“out of sample”问题,但非局部信息在此过程中被忽略,即算法没有考虑相隔较远的点之间的关系。2007年,Yang等人提出了非监督判别投影(Unsupervised discriminant projection,UDP)算法[8]。该方法考虑了样本点在低维表示后的局部和非局部性,最小化局部散度的同时最大化非局部散度,即使非局部散度与局部散度的比值尽可能大。但UDP是非监督的学习方法,也就是不能利用样本的类别信息,不利于分类;而且在处理过程中也出现小样本问题[9]:当训练样本个数远小于样本维数时,就会出现矩阵奇异问题。2012年,楼宋江等人提出的小样本有监督拉普拉斯判别分析算法(Supervised Laplacian discriminant analysis, SLDA)[9], 通过将类内拉普拉斯散度矩阵投影在去除零空间的总体拉普拉斯散度矩阵上,避免了小样本问题。但是由于该方法中没有明确最大化类间散度,因而导致在投影空间的可分性不够好。2015年,丁春涛等人提出的基于双邻接图的判别近邻嵌入算法(Double adjacency graphs-based discriminant neighborhood embedding, DAG-DNE)[10], 融入了构建双邻接图的想法,解决了判别近邻嵌入(Discriminant neighborhood embedding, DNE)图嵌入降维方法在构造权重矩阵时数据不平衡的问题。
受到DAG-DNE算法的启发,本文提出了一种新的基于拉普拉斯判别分析的有监督降维方法,称为适用于小样本的双邻接图判别分析方法(Double adjacent graph-based discriminant analysis for small sample size, DAG-DA)。DAG-DA在构建邻接图时考虑了样本的不平衡问题,每个样本点都至少建立两个关联,并将局部拉普拉斯散度矩阵与非局部拉普拉斯散度矩阵的差投影到总体拉普拉斯散度矩阵的秩空间中,然后在该空间中进行特征问题的求解,求得投影矩阵。通过在简单人工数据集、Yale人脸库和ORE人脸库的实验证明了DAG-DA算法的优越性。
1 适用于小样本的SLDA算法针对小样本问题,已有相应的一些解决方案[9, 11-12],其中监督化拉普拉斯判别分析算法和本文的工作紧密相关。该算法是一种有监督的流形学习算法,其目标是最小化局部散度,同时最大化非局部散度,即非局部散度与局部散度的比值尽可能大[13],表达式为
| $ \max J\left( \mathit{\boldsymbol{W}} \right) = \frac{{{J_{\rm{N}}}\left( \mathit{\boldsymbol{W}} \right)}}{{{J_{\rm{L}}}\left( \mathit{\boldsymbol{W}} \right)}} \Leftrightarrow \min J\left( \mathit{\boldsymbol{W}} \right) = \frac{{{J_{\rm{L}}}\left( \mathit{\boldsymbol{W}} \right)}}{{{J_{\rm{T}}}\left( \mathit{\boldsymbol{W}} \right)}} $ | (1) |
式中:W为投影矩阵,JL为局部散度,JN为非局部散度,JT为总体散度,JT=JL+JN。
以上优化问题(1)可以转化为如下目标函数
| $ {\mathit{\boldsymbol{S}}_{\rm{L}}}\mathit{\boldsymbol{w = }}\lambda {\mathit{\boldsymbol{S}}_{\rm{T}}}\mathit{\boldsymbol{w}} $ | (2) |
式中:λ为特征分解得到的特征值,w为特征向量,SL为局部拉普拉斯散度矩阵,ST为丢弃零空间的总体拉普拉斯散度矩阵。
2 适用于小样本的DAG-DA算法 2.1 双邻接图判别分析由于适用于小样本的监督化拉普拉斯判别分析算法在分子上仅考虑将局部拉普拉斯散度矩阵进行投影, 忽略了非局部拉普拉斯散度矩阵。为了强调非局部信息,本文考虑在最优化函数里引入非局部散度, 表达式为
| $ \min J\left( \mathit{\boldsymbol{W}} \right) = \frac{{{J_{\rm{L}}}\left( \mathit{\boldsymbol{W}} \right) - {J_{\rm{N}}}\left( \mathit{\boldsymbol{W}} \right)}}{{{J_{\rm{T}}}\left( \mathit{\boldsymbol{W}} \right)}} = \frac{{{J_D}\left( \mathit{\boldsymbol{W}} \right)}}{{{J_{\rm{T}}}\left( \mathit{\boldsymbol{W}} \right)}} $ | (3) |
局部散度为
| $ {J_{\rm{L}}} = \frac{1}{{2nn}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{F_{ij}}{{\left( {{y_i} - {y_j}} \right)}^2}} } $ | (4) |
非局部散度为
| $ {J_{\rm{N}}} = \frac{1}{{2nn}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{B_{ij}}{{\left( {{y_i} - {y_j}} \right)}^2}} } $ | (5) |
式(4, 5)中:F为相似度矩阵;B为差异度矩阵。与SLDA方法从数据点的K近邻中找到同类和异类样本点来构建邻接图不同,本文在构造邻接图时借用双邻接图的思想,从同类和异类样本点间分别找到K个近邻点,再构建F和B。
设样本集{(xi, yi)}i=1n,其中xi∈ Rd,yi∈{1, 2, …, c}为xi的类别标签,n为样本的个数,d为样本的维数,c为类别总数。对于这个样本集,利用样本的类别信息,对每一个数据点都构造相似度矩阵F和差异度矩阵B,根据样本分布赋予不同的权值,表达式为
| $ {F_{ij}} = \left\{ \begin{array}{l} \exp \left\{ { - \frac{{{\mathit{\boldsymbol{x}}_i} - \mathit{\boldsymbol{x}}_j^2}}{t}} \right\}\;\;\;{\mathit{\boldsymbol{x}}_i} \in N_k^ + \left( j \right)\;或\;{\mathit{\boldsymbol{x}}_j} \in N_k^ + \left( i \right)\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (6) |
| $ {B_{ij}} = \left\{ \begin{array}{l} - \exp \left\{ { - \frac{{{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right\|}^2}}}{\sigma }} \right\}\;\;\;{\mathit{\boldsymbol{x}}_i} \in N_k^ - \left( j \right)\;或\;{\mathit{\boldsymbol{x}}_j} \in N_k^ - \left( i \right)\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (7) |
式中:Nk+(i)和Nk+(j)分别表示样本xi和xj的同类近邻集合,且xi和xj类别相同;Nk-(i)和Nk-(j)分别表示样本xi和xj的异类近邻集合,且xi与xj类别不相同;t和σ为可变参数。由式(6, 7)可以看出,当同类样本距离越近,它们的相似度越高,反之亦然。当异类样本距离越近,它们的差异度越小,反之亦然。
由式(4, 6)可以得到
| $ {J_{\rm{L}}} = \frac{1}{{2nn}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{F_{ij}}{{\left( {{y_i} - {y_j}} \right)}^2}} } = \frac{1}{{nn}}{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{\rm{L}}}\mathit{\boldsymbol{W}} $ | (8) |
式中SL为局部拉普拉斯散度矩阵
| $ {\mathit{\boldsymbol{S}}_{\rm{L}}} = \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{F_{ij}}\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right){{\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right)}^{\rm{T}}}} } = \mathit{\boldsymbol{XF'}}{\mathit{\boldsymbol{X}}^{\rm{T}}} - \mathit{\boldsymbol{XF}}{\mathit{\boldsymbol{X}}^{\rm{T}}} = \mathit{\boldsymbol{XL}}{\mathit{\boldsymbol{X}}^{\rm{T}}} $ | (9) |
式中F′为一个对角矩阵,对角线上的元素为:
同样,由式(5,7)可以得到
| $ {J_{\rm{N}}} = \frac{1}{{2nn}}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{B_{ij}}{{\left( {{y_i} - {y_j}} \right)}^2}} } = \frac{1}{{nn}}{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{\rm{N}}}\mathit{\boldsymbol{W}} $ | (10) |
| $ {\mathit{\boldsymbol{S}}_{\rm{N}}} = \frac{1}{2}\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {{B_{ij}}\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right){{\left( {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{x}}_j}} \right)}^{\rm{T}}}} } = \mathit{\boldsymbol{XB'}}{\mathit{\boldsymbol{X}}^{\rm{T}}} - \mathit{\boldsymbol{XB}}{\mathit{\boldsymbol{X}}^{\rm{T}}} = \mathit{\boldsymbol{XN}}{\mathit{\boldsymbol{X}}^{\rm{T}}} $ | (11) |
式中:B′为一个对角矩阵,对角线上的元素为
由式(3, 8, 10)可推导出目标函数等价于
| $ \min \frac{{{J_{\rm{D}}}\left( \mathit{\boldsymbol{W}} \right)}}{{{J_{\rm{T}}}\left( \mathit{\boldsymbol{W}} \right)}} = \frac{{{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{\rm{D}}}\mathit{\boldsymbol{W}}}}{{{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{\rm{T}}}\mathit{\boldsymbol{W}}}} = \frac{{{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{\rm{D}}}\alpha }}{{{\mathit{\boldsymbol{\alpha }}^{\rm{T}}}{\mathit{\boldsymbol{S}}_{\rm{T}}}\mathit{\boldsymbol{\alpha }}}} \Leftrightarrow {\mathit{\boldsymbol{S}}_{\rm{D}}}\mathit{\boldsymbol{w = }}\lambda {\mathit{\boldsymbol{S}}_{\rm{T}}}\mathit{\boldsymbol{w}} $ | (12) |
式中:SD =SL-SN,α∈range (ST)。
2.2 秩空间首先对ST进行特征分解。由于总体拉普拉斯散度矩阵ST非负定,所以对它进行特征值分解后的特征值可能为零,可能为正。取非零的特征值
| $ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = {\rm{diag}}\left( {{\lambda _1},{\lambda _2}, \cdots ,{\lambda _r},{\lambda _{r + 1}}, \cdots ,{\lambda _n}} \right) $ |
其中特征值λ1≥λ2…≥λr,λr+1=λr+2=…=λn=0。特征值对应的特征向量矩阵为
| $ \mathit{\boldsymbol{U}} = \left\{ {{\mathit{\boldsymbol{u}}_1},{\mathit{\boldsymbol{u}}_2}, \cdots ,{\mathit{\boldsymbol{u}}_r},{\mathit{\boldsymbol{u}}_{r + 1}}, \cdots ,{\mathit{\boldsymbol{u}}_n}} \right\} $ |
其中特征值λi对应的特征向量为ui。
令非负特征值矩阵
| $ {{\mathit{\boldsymbol{\tilde S}}}_D} = \mathit{\boldsymbol{W}}_1^{\rm{T}}{\mathit{\boldsymbol{S}}_{\rm{D}}}{\mathit{\boldsymbol{W}}_1} $ | (13) |
因为差异拉普拉斯散度矩阵SD也是非负定的,所以对它进行特征值分解后的特征值可能为零,也可能为正。设分解后d个最小的特征值为μ1≤μ2≤…≤μd,其对应向量分别为φ1, φ2, …, φd,令W2= {φ1, φ2, …, φd}。最终的投影矩阵W =W1W2。DAG-DA算法的步骤如下:
输入:训练样本集合{(xi, yi)}i=1n,令样本矩阵为X=[x1, x2, …, xn]∈ R d×n,降维子空间维数r。
输出:投影矩阵W∈ Rd×r。
(1) 构建相似度矩阵S和差异性矩阵B;
(2) 计算局部拉普拉斯散度矩阵SL,非局部拉普拉斯散度矩阵SN,以及它们的和ST与差SD;SL=XLXT, 其中L=S′-S,S′为对角矩阵,
(3) 对矩阵ST进行特征分解,取其非零特征值λi和非零特征值对应的向量ui,分别组成矩阵Λ和U,其中Λ为对角矩阵且Λii=λi,U的第i列为ui,令W1=UΛ;
(4) 将SD在W1上投影,得到
(5) 得到最终投影矩阵:W=W1W2。
2.3 DAG-DA算法和SLDA算法比较(1) 在用邻接图来保持样本的局部结构信息时,SLDA算法找到近邻后,利用类别信息再构建类内和类间邻接图,这样可能会出现只有类内近邻或只有类间近邻的数据不平衡问题。而在计算权值时,同等距离下类间近邻比类内近邻的权值更大,这显然不利于保持数据的结构。DAG-DA算法分别在类内和类间找近邻点,从热核函数可以看出:若是类内近邻点,则赋予较大的权值;若是类间近邻点,则权值较小。这样可以扩大类内距离缩小类间距离的影响,同时也解决了数据不平衡的问题,更好地保持了数据的流形结构。
(2) 在优化问题选取目标函数时,SLDA算法的目标函数(式(1))分子上仅考虑了将局部拉普拉斯散度矩阵进行投影,而忽略了非局部拉普拉斯散度矩阵; 而DAG-DA算法在最优化函数(式(3))里引入了非局部散度,强调了类间散度,使得降维后的数据可分性更好。
(3) 在对总体拉普拉斯散度矩阵进行特征分解后,SLDA算法选取的投影空间为特征向量乘以一个小于1的数; 而DAG-DA算法直接将非零向量作为投影空间,相当于少乘一个缩小因子,使数据更加准确。
3 实验结果与分析为验证DAG-DA算法的有效性,在各类数据上对DAG-DA算法进行实验,并与SLDA算法、LPP算法和DNE算法进行比较。这4种算法均可以对近邻个数进行调节,其中SLDA算法和DAG-DA算法中的t和σ为可变参数。本文实验均采用最近邻分类器对降维后的数据进行分类。
3.1 人工数据随机生成两类符合均匀分布的人工数据,一类是0~1之间的随机数,另一类是0.7~1.7之间的随机数,分别用SLDA算法和DAG-DA算法学习得到投影矩阵。图 1显示了SLDA算法和DAG-DA算法学习投影矩阵后投影后的效果。从图 1中看到,图 1(b)中的类间点距离更大,类内点距离更小,也就是DAG-DA算法相对比SLDA而言,降维效果有了明显的提升,也更适合于分类。在对优化函数进行等价替代后,SLDA算法的目标函数里并没有考虑类间距离,仅将局部拉普拉斯散度矩阵投影到总空间。DAG-DA算法对其进行改进,将局部拉普拉斯散度矩阵与非局部拉普拉斯散度矩阵的差进行投影,是一个更理想的目标函数。
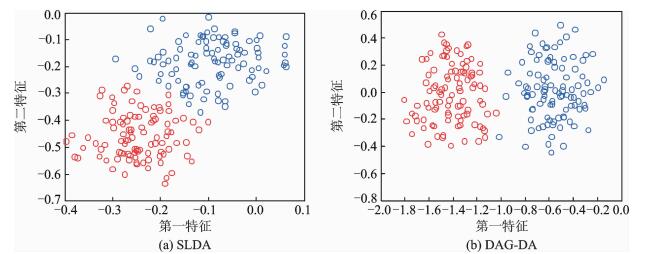
|
图 1 SLDA与DAG-DA在简单人工数据集上的比较 Fig. 1 Comparison of SLDA and DAG-DA on artificial dataset |
除了图 1能直观地看出两种算法的分类效果外,表 1还给出了两种算法在人工数据测试后的具体结果。从表 1中可以看出,用DAG-DA算法降维比SLDA算法得到的类内距离和更小,类间距离和更大,说明降维后分类效果更佳。
| 表 1 SLDA与DAG-DA在人工数据上测试结果比较 Tab. 1 Test results of SLDA and DAG-DA on artificial dataset |
3.2 Yale人脸数据库
Yale人脸数据库[14]共有165张人脸灰度图像,每张图像数字为32×32的像素矩阵,来自15个不同的人,每人11张。每个人的各张图像有不同的光照条件(中央光照、左侧光照、右侧光照)和不同的表情(眼镜/无眼镜、高兴、常态、悲伤、睡眠、惊讶和眨眼)。Yale人脸数中不同条件下的一些人脸图像样本如图 2所示。该实验中,随机选择60%样本作为训练样本,其余的40%作为测试样本。

|
图 2 Yale人脸图像示例 Fig. 2 Face examples of Yale dataset |
在实验时,为了减少大量的计算,先采用PCA方法对测试数据进行初始降维,初始降维的投影矩阵为A。再采用DAG-DA,SLDA,LPP,DNE四种算法进行再次降维,二次降维矩阵为W,最终投影矩阵为P = WA。利用P把训练样本和训练样本投影到低维空间,再用近邻分类器进行分类,得到各个方法降维后的识别率。在构造邻接图时,选取k=3,通过循环找到最佳的t和σ。图 3显示了DAG-DA算法,SLDA算法,LPP算法和DNE算法在不同维数下的识别率。表 2显示了不同算法在Yale人脸库上的最高识别率和特征维度。

|
图 3 在Yale人脸库上不同维数的识别率 Fig. 3 Recognition rate of different algorithms on Yale dataset |
| 表 2 Yale人脸库各算法最高识别率和特征维数 Tab. 2 Recognition rate and dimension of different algorithms on Yale dataset |
3.3 ORL人脸数据库
ORL人脸数据库[15]共有400张人脸灰度图像,每张图像为32×32的像素矩阵,来自40个不同的人,每人10张。每个人的各图像有不同的人脸大小、人脸旋转程度和不同的表情(睁眼/闭眼、高兴/悲伤、戴眼镜/不戴眼镜等)。ORL人脸数据库中不同条件下的一些人脸图像样本如图 4所示。该实验中,随机选择60%样本作为训练样本,其余的40%作为测试样本。

|
图 4 ORL人脸图像示例 Fig. 4 Face examples of ORL dataset |
同样,为了减少大量的计算,先采用PCA方法对测试数据进行初始降维,再采用DAG-DA,SLDA,LPP和DNE四种算法进行再次降维,最后用近邻分类器进行分类,得到各个方法降维后的识别率。本文选取k=3,通过循环找到最佳的t和σ。图 5显示了DAG-DA算法,SLDA算法,LPP算法和DNE算法在不同维数下的识别率。表 3显示了不同算法在ORL人脸库上的最高识别率和特征维度。
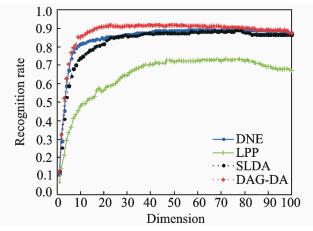
|
图 5 在ORL人脸库上不同维数的识别率 Fig. 5 Recognition rate of different algorithms on ORL dataset |
| 表 3 ORL人脸库各算法最高识别率和特征维数 Tab. 3 Recognition rate and dimension of different algorithms on ORL dataset |
从实验结果可以看出,DAG-DA算法达到的最佳识别率最高。SLDA算法的识别率高于LPP算法,因为SLDA算法考虑了非局部信息和样本的类别信息。DNE算法也是监督化学习方法,它构建了类内与类间的邻接图,让同类数据在低维空间紧凑,不同类数据尽可能分开,识别率高于LPP算法。DAG-DA算法不仅考虑了非局部信息和样本类别信息,而且考虑了数据不平衡问题,并在目标函数内加入了非局部拉普拉斯散度矩阵,所以最佳识别率不仅优于LPP算法,也比SLDA和DNE算法更胜一筹。
4 结束语本文为了处理监督化拉普拉斯判别分析方法中的邻接图数据不平衡问题,以及目标函数中类间信息缺失问题,提出了适用于小样本的双邻接图判别分析算法DAG-DA,并在Yale和ORL人脸数据集上验证了该方法的有效性。
但是,本文算法在实现过程中需要寻找热核函数的最佳参数值,同时去掉了总体拉普拉斯散度矩阵的零空间,这两步使得该算法的时间复杂度比LPP和DNE算法高。下一步工作将尝试寻找时间复杂度较低且降维效果好的算法。
| [1] |
Jolliffe I T. Principal component analysis[M]. Berlin: Springer-Verlag, 2002.
|
| [2] |
Yan S, Xu D, Zhang B, et al. Graph embedding and extensions:A general framework for dimensionality reduction[J]. IEEE Trans Pattern Anal Mach Intell, 2006, 29(1): 40. |
| [3] |
Tenenbaum J B, De S V, Langford J C. A global geometric framework for nonlinear dimensionality reduction[J]. Science, 2000, 290(5500): 2319-2323. DOI:10.1126/science.290.5500.2319 |
| [4] |
Belkin M, Niyogi P. Laplacian Eigenmaps for dimensionality reduction and data representation[J]. Neural Computation, 2003, 15(6): 1373-1396. DOI:10.1162/089976603321780317 |
| [5] |
Roweis S T, Saul L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2009, 290(5500): 2323-2326. |
| [6] |
Niyogi X. Locality preserving projections[J]. Advances in Neural Information Processing Systems, 2004, 16: 153. |
| [7] |
He X, Cai D, Yan S, et al. Neighborhood preserving embedding[C]//Tenth IEEE International Conference on Computer Vision. [S. l. ]: IEEE, 2005: 1208-1213.
|
| [8] |
Yang J, Zhang D, Yang J, et al. Globally maximizing, locally minimizing:Unsupervised discriminant projection with applications to face and palm biometrics[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(4): 650-664. DOI:10.1109/TPAMI.2007.1008 |
| [9] |
楼宋江, 张国印, 潘海为, 等. 人脸识别中适合于小样本情况下的监督化拉普拉斯判别分析[J]. 计算机研究与发展, 2012, 49(8): 1730-1737. Lou Songjiang, Zhang Guoyin, Pan Haiwei, et al. Supervised Laplacian discriminant analysis for small sample size problem with its application to face recognition[J]. Journal of Computer Research and Development, 2012, 49(8): 1730-1737. |
| [10] |
Ding C T, Zhang L. Double adjacency graphs-based discriminant neighborhood embedding[J]. Pattern Recognition, 2015, 48(5): 1734-1742. DOI:10.1016/j.patcog.2014.08.025 |
| [11] |
Huang R, Liu Q, Lu H, et al. Solving the small sample size problem of LDA[C]//16th International Conference on Pattern Recognition. [S. l. ]: IEEE Computer Society, 2002: 30029.
|
| [12] |
Jain A K, Duin R P W, Mao J. Statistical pattern recognition:A review[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2000, 22(1): 34-37. |
| [13] |
Tao Y J, Yang J. Quotient vs. difference:Comparison between the two discriminant criteria[J]. Neurocomputing, 2010, 73(10/11/12): 1808-1817. |
| [14] |
University of California, San Diego. The Yale face database[EB/OL]. http://vision.ucsd.edu/content/yale-face-database, 2013-12-21.
|
| [15] |
AT&T Laboratories Cambridge. The ORL face database[EB/OL]. http://www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html, 2013-12-21.
|
 2018, Vol. 33
2018, Vol. 33

