线性判别分析(Linear discriminant analysis, LDA)是一种流行的有监督数据降维和可视化工具, 广泛用于模式识别和机器学习等各个领域[1-2]; 它最大化类间散度的同时最小化类内散度, 提取数据特征, 将高维投影到2~3维即获得可视化, 能更直观理解和探索潜在的数据结构[3], 有利于其后续的分类算法获得更好的泛化性能。判别分析可分为线性型和非线性型两大类, 上述提及的LDA[4]是线性型的代表之一, 而传统的非线性判别方法主要包括神经网络和核方法, 如核LDA(Kernel linear discriminant analysis, KLDA)[5], 流形判别分析[6], (深度)神经网络[7-8]和深度判别分析[9]等。其中KLDA采用核函数将输入样本映射到高维特征空间, 而后利用LDA进行线性分类。而神经网络(Neural network, NN)则通过多层结构的非线性变换将输入映射到输出空间以实现非线性判别。尽管NN缺乏核方法那样的简洁表示方式, 但NN所具有的分布并行特点和其对连续函数的万能逼近性使其获得了广泛应用。事实上, 基于NN的判别分析可追溯到1995年Mao和Jain的先驱性工作[10], 即神经网络判别分析方法(Neural networks discriminant analysis, NNDA), 该工作促发了众多非线性化分类和可视化研究。目前该文被引数已超680次, 并在1996年获得了IEEE TNN期刊年度最佳论文奖[11]。然而, 与其他多层前向网络训练类似, NNDA存在优化收敛速度慢、易陷入局部最小、且因网络结构复杂易导致过拟合等问题。1999年由Scholkopft等人[12]提出的KLDA, 利用核技巧避免了NNDA复杂的优化。相对NNDA, 其判别投影仅需通过求解一广义特征值方程即可获得解析解, 不仅快速而且学习性能优良, 因而受到广泛关注和应用, 该工作目前的引用数已超2 240次。
然而传统的KLDA在学习过程中存在数据的可伸缩性问题[13], 当数据量增加到一定规模后, 算法所学得的判别方向复杂度与训练样本数成线性增长, 这在常规计算资源上已难以胜任相应的学习。相比KLDA的这种复杂性, 本文所提出的ENDA算法本身只线性于隐节点数, 而独立于训练样本数, 在现实应用中, 隐节点数通常比训练样本数要小很多。因此, 当实验数据规模变大时, 在保证分类性能的前提下, ENDA计算成本比KLDA更小。另一方面, 近年来的众多研究表明[14], 对传统NN(如卷积网络)的深化学习能大大提升图像分类[8]、语音识别[15]和自然语言处理[16]等的识别性能, 由此也促发了对NNDA向深度化学习[17]的研究, 在对NNDA的跟踪研究发现, 此类研究主要有两大趋势:(1)网络变大变深的深度学习; (2)限于常规计算资源的加速化(例如典型ELM)极速学习。然而深度学习的成功往往需付出高昂的代价, 是因为:(1)深度学习需要学习大量参数, 样本少了很易“过拟合”, 数据大小成为其性能提升的关键[18]; (2)模型复杂化需要庞大的计算资源和巨大的时间开销。而“没有免费午餐定理”告诉人们:算法的优劣必须针对具体的学习任务, 其有效性必须考虑“偏好”问题, 结果是:(1)时间开销大和计算资源缺乏, 即难以在常规计算资源下完成深度学习; (2)所需要的大数据的标记涉及昂贵的人力和物力等问题。综上所述, 当数据规模达不到深度学习要求的情况下(在机器学习UCI储存数据库公布的348个数据集当中, 296个数据集的主要样本例数集中在50 000个以下, 约占85%), 如何在常用PC计算资源下进行更有效的学习变得更有意义和更加紧迫, 所以笔者更偏重于NN加速化的研究。在保证分类性能的前提下, ENDA能迅速处理这类常规数据的分类任务, 与传统NNDA不同是因为其利用了快速、可靠的随机映射。
最新研究表明[19]使用随机投影的简单NN与人类学习具有很大相关性和相似鲁棒性。因此也为10年前采用此原理的极速学习机(Extreme learning machine, ELM)提供了认知原理上的解释, 尽管ELM被提出以来得到了广泛关注, 并已在特征学习、分类、回归和聚类[20]等方面获得了一系列拓展, 但就笔者所知, 还未有对NNDA相应的ELM改造。本文基于这一事实, 对NNDA进行极速化, 构建出一种极速非线性判别分析方法(Extreme nonlinear discriminant analysis, ENDA), 使其兼具NNDA的万能逼近能力和KLDA能解析获得全局最优解的快速性。最后在UCI机器学习库真实数据集上进行实验, 结果显示ENDA比KLDA和NNDA具有更优的分类性能。
1 极速学习机模型极限学习机ELM[21]是一种特殊单隐层前向神经网络(Single-hidden layer feedforward neural networks, SLFN), 由Huang等人于2004年提出, 目前已获得了1 180多次引用。不同于SLFN传统梯度下降学习算法, ELM随机产生输入层到隐层权重和偏置, 克服SLFN反复迭代计算导致的收敛慢、且不能保证全局最优解等问题。在优化隐节点和输出节点的权重上, ELM采用正则化最小二乘法快速求得闭合解[22]。ELM由输入层, 隐层和输出层3层网络组成, 其中隐节点常用非线性激活函数。典型的非线性激活函数包括Sigmoid函数、高斯函数和径向基函数。不失一般性, 这里采用式(1)中的Sigmoid函数作为隐层神经元的激活函数
| $ g\left( x \right) = \frac{1}{{1 + \exp \left( { - x} \right)}} $ | (1) |
ELM不仅有速度上优势, 更重要的是理论上也证明了其具有与SLFN同样的对非线性分段连续函数的万能逼近能力[23]。其学习过程可视为两步:(1)确定网络NN隐层的神经元数, 随机设置输入权重和偏差; (2)确定网络权重。在特征空间中通过使训练误差平方和最小解析求得输出权重的最小范数解, 达到优化输出权重的目的。ELM除了快速外还能实现对不同类型数据的分析, 并已渐渐成为一种新型的快速学习范式。
现设有N个样本的训练数据集
| $ {h_i}\left( {{\mathit{\boldsymbol{x}}_j}} \right) = g\left( {\mathit{\boldsymbol{w}}_i^{\left( 1 \right){\rm{T}}}{\mathit{\boldsymbol{x}}_j} + {b_i}} \right) $ | (2) |
式中:wi(1)=[wi1(1), wi2(1), …, win(1)]T(i=1, …, L, j=1, …, N)为输入层连接第i个隐层单元输入权值, bi为偏置。定义H为L维的隐层映射特征空间表示
| $ \mathit{\boldsymbol{H}}\left( {{\mathit{\boldsymbol{w}}_1},{\mathit{\boldsymbol{w}}_2}, \cdots ,{\mathit{\boldsymbol{w}}_L},{b_1},{b_2}, \cdots ,{b_L},{\mathit{\boldsymbol{x}}_1},{\mathit{\boldsymbol{x}}_2}, \cdots ,{\mathit{\boldsymbol{x}}_N}} \right) =\\ {\left[ {\mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_1}} \right),\mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_2}} \right), \cdots ,\mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_N}} \right)} \right]^{\rm{T}}} \in {{\bf{R}}^{N \times L}} $ | (3) |
式中:
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_B {L_{{\rm{ELM}}}} = \frac{1}{2}{{\left\| \mathit{\boldsymbol{B}} \right\|}^2} + \frac{C}{2}\sum\limits_{j = 1}^N {{{\left\| {{\mathit{\boldsymbol{\xi }}_j}} \right\|}^2}} }\\ {{\rm{s}}.\;{\rm{t}}.\;\;\;\mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_j}} \right)\mathit{\boldsymbol{B}} = \mathit{\boldsymbol{t}}_j^{\rm{T}} - \mathit{\boldsymbol{\xi }}_j^{\rm{T}}\;\;\;\;j = 1, \cdots ,N} \end{array} $ | (4) |
式中:ξj为第j个训练模式的误差, B= [β1, …, βL]T∈ RL×m, C>0为惩罚系数。而ELM的输出方程为
| $ f\left( {{\mathit{\boldsymbol{x}}_j}} \right) = \sum\limits_{i = 1}^L {{\mathit{\boldsymbol{\beta }}_i}g\left( {\mathit{\boldsymbol{w}}_i^{\rm{T}}{\mathit{\boldsymbol{x}}_j} + {b_i}} \right)} = \mathit{\boldsymbol{h}}\left( {{\mathit{\boldsymbol{x}}_j}} \right)\mathit{\boldsymbol{B}} $ | (5) |
式中βi=[βi1, βi2, …, βim]T为输出权重。因此最终优化问题式(4)可重写为
| $ \mathop {\min }\limits_B {\mathit{\boldsymbol{L}}_{{\rm{ELM}}}} = \frac{1}{2}{\left\| \mathit{\boldsymbol{B}} \right\|^2} + \frac{C}{2}\sum\limits_{j = 1}^N {{{\left\| {\mathit{\boldsymbol{T}} - \mathit{\boldsymbol{HB}}} \right\|}^2}} $ | (6) |
式中T=[t1, …, tN]T∈ RN×m。借助正则化最小二乘法求解获得全局最优的权阵B为
| $ \mathit{\boldsymbol{B}} = {\left( {\frac{\mathit{\boldsymbol{I}}}{C} + {\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{H}}} \right)^{ - 1}}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{T}} $ | (7) |
式中I为单位矩阵。利用式(7)可快速计算B[22]。ELM从理论和经验上获得了性能保证[24]。借助其思想, 拟对由Mao和Jain所提出的NNDA进行极速化改造, 建立ENDA模型。
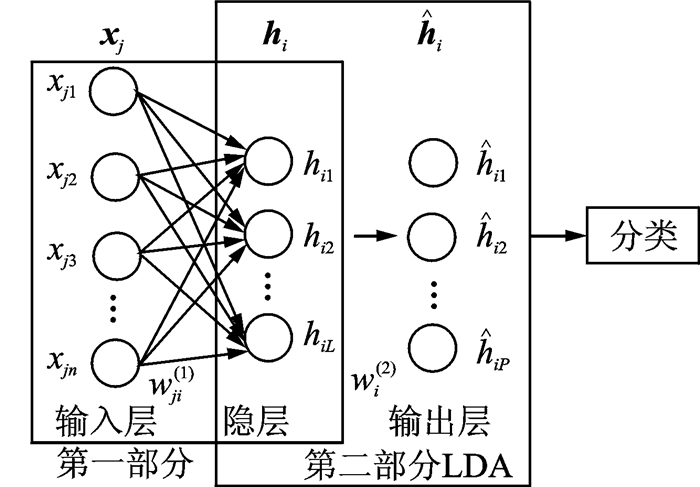
2 极速非线性判别分析网络Mao等人的NNDA属于浅层网络, 其目标是学习非线性降维, 但其遗传了SLFN的训练慢、易陷于局部最优的缺点。同时基于深度学习思想实现的多层ELM[25-26], 能够实现对海量数据的建模, 尽管能获得比深度网络相对快的训练, 但对本文所要处理的数据规模仍显得“大材小用”, 偏离了传统ELM简单易解的特性。本文目的在于极速化NNDA, 使ENDA在常规计算设施上能处理比NNDA更大规模的数据集, 同时继承了ELM能解析求解的优点。ENDA网络结构如图 1所示, 具体分两步:(1)随机生成NN的输入层连接权重和偏置, 构成了一个随机映射, 结果使模型具有简单快速性; (2)视隐层输出为新形成的训练数据, 用LDA准则优化进输出层连接权重, 同时可用于可视化。同ELM求解一样, 不仅无局部最小, 并且能快速解析求得全局闭合最优解, 最后形成一个新的判别特征空间, 而后用所获特征对目标进行分类。由于采用了随机非线性变换和后续的判别优化, 使ENDA对数据有着自适应性和期望的分类性能。
|
图 1 ENDA网络结构图 Fig. 1 Structure of ENDA Network |
ENDA算法第一部分实现原始特征X=[x1T, x1T, …, xNT]∈ RN×n]到非线性特征H=[h1T, h2T, …, hNT]∈ RN×L的极速随机映射; 第二部分通过使用LDA对H进行降维。LDA作为一种有效的降维和分类方法, 具有以下优点:(1)可作为可视化工具; (2)通过获取最佳投影方向问题转化为求解最大特征值的问题, 易求得分类面法方向的解析解。在多分类任务中, 假定一个有包含c类的样本, LDA降维实际是从L维空间向P维空间投影, 设P≤c-1。对H经过式(9)投影后得到新样本
| $ \mathit{\boldsymbol{W}} = \left[ {\mathit{\boldsymbol{w}}_1^{\left( 2 \right)},\mathit{\boldsymbol{w}}_2^{\left( 2 \right)}, \cdots ,\mathit{\boldsymbol{w}}_P^{\left( 2 \right)}} \right] $ | (8) |
| $ \mathit{\boldsymbol{\hat H}} = {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{H}} $ | (9) |
式中wi(2)为LDA的投影权重。样本总类内散度矩阵Sb和类间散度矩阵Sw分别定义为
| $ {\mathit{\boldsymbol{S}}_b} = \sum\limits_{i = 1}^c {{n_i}\left( {{\mathit{\boldsymbol{\mu }}_i} - \mathit{\boldsymbol{\mu }}} \right){{\left( {{\mathit{\boldsymbol{\mu }}_i} - \mathit{\boldsymbol{\mu }}} \right)}^{\rm{T}}}} $ | (10) |
| $ {\mathit{\boldsymbol{S}}_w} = \sum\limits_{i = 1}^c {\sum\limits_{\hat h \in {{\mathit{\boldsymbol{\hat H}}}_i}} {\left( {\mathit{\boldsymbol{\hat h}} - {\mathit{\boldsymbol{\mu }}_i}} \right){{\left( {\mathit{\boldsymbol{\hat h}} - {\mathit{\boldsymbol{\mu }}_i}} \right)}^{\rm{T}}}} } $ | (11) |
式中:
| $ \mathop {\max }\limits_W \mathit{\boldsymbol{J}}\left( \mathit{\boldsymbol{W}} \right) = \frac{{\left| {{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_b}\mathit{\boldsymbol{W}}} \right|}}{{\left| {{\mathit{\boldsymbol{W}}^{\rm{T}}}{\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{W}}} \right|}} $ | (12) |
然后对其进行判别分析求解, 最大化J(W)等价于求解如下广义特征问题, 即
| $ {\mathit{\boldsymbol{S}}_b}\mathit{\boldsymbol{W}} = \lambda {\mathit{\boldsymbol{S}}_w}\mathit{\boldsymbol{W}} $ | (13) |
通过求解式(13)可计算出LDA投影矩阵W, 它由Sw-1Sb的c-1个最大广义特征值所对应的特征向量组成, 此W即为最佳的判别投影矩阵。通过以上两部分计算可得到整个ENDA投影权重, 完整的ENDA算法如算法1所示。
算法1 ENDA算法
输入:样本集N={ (xj, tj)|xj∈ Rn, tj∈ Rm}j=1N, 激活函数g(·), 隐层节点数L。
输出:ENDA输出
步骤1 随机生成ENDA第一部分中的权重wi(1)和偏置bi, i=1, …, L;
步骤2 计算ENDA的隐层输出hi (通过式(2));
步骤3 对隐层输出hi进行判别分析, 通过式(13)计算出投影权重W, 得到ENDA的输出
实验环境如下:MATLAB2013a, Intel(R) CoreTM i5-3470 CPU @3.20 GHz, 16.0 GB内存, 64位Win10操作系统。如表 1所示, 实验所用数据为UCI(http://archive.ics.uci.edu/ml/)数据集。实验前需对数据进行了归一化, 然后将处理后的数据作为ENDA的输入进行训练。为了验证模型的有效性, 将ENDA算法与NNDA, KLDA, ELM算法进行了比较分析, 为公平起见, NNDA, ELM与ENDA的隐层节点参数相同, 统一使用K近邻算法(K-Nearest Neighbor), 分别对NNDA, KLDA和ENDA进行分类。实验过程中参数K采用10折交叉验证。
| 表 1 UCI数据集 Tab. 1 UCI datasets |
按照Mao等人提出NNDA方法实验, 采用的NN包含两个隐层的误差反向传播算法(Error back propagation, BP)网络, 输入层节点个数对应特征维数, 输出层神经元个数等于类别数。通过反向传播学习算法训练前馈神经网络两个隐层的权重, 并且固定最后隐层的节点数作为要投影空间的维度。NN训练参数设置如下:学习率为0.7, 迭代次数5 000次, 动量因子为0.3, 最小误差为0.001。KLDA所采用的高斯映射核函数的类型为K(x, y)=exp(
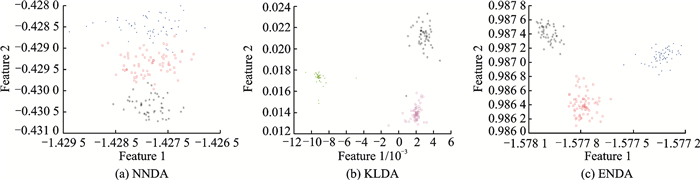
为验证ENDA模型的非线性特征学习能力, 实验中随机抽取UCI的4组数据集通过模型投影到二维空间进行可视化, 结果如图 2~5所示。
|
图 2 Wine数据集的可视化 Fig. 2 Wine datasetvisualized by three algorithms |
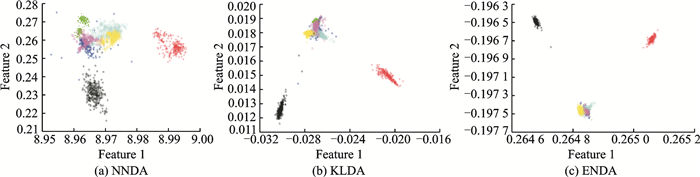
|
图 3 Segment数据集的可视化 Fig. 3 Segment dataset visualized by three algorithms |

|
图 4 Waveform3数据集的可视化 Fig. 4 Waveform3 dataset visualized by three algorithms |
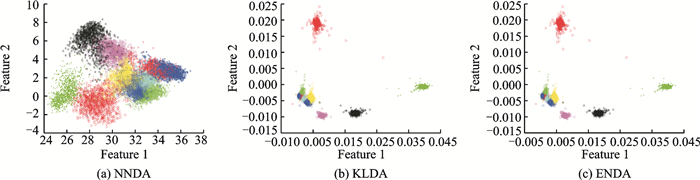
|
图 5 Pen-Digits数据集的可视化 Fig. 5 Pen-Digits dataset visualized by three algorithms |
由图 2~5可以观察到样本分别经过NNDA, ENDA和KLDA方法投影二维投影空间后的效果:数据经过投影之后都具有最大的分离度, 其中ENDA和KLDA投影分类效果更直观有效。同时实验结果表明对数据线性不可分问题, 非线性变换是一个强大的方法。
在隐节点参数设置相同情况下, NNDA不仅花费的训练时间更长, 而且投影出来效果分离程度并不明显, 如图 4, 5所示, 其原因有:(1)NNDA最后隐层到输出层训练权重并没有充分利用; (2)NNDA为避免扭曲严重, 以线性函数替代Sigmoid函数。在图 4, 5中, 随着数据规模和特征属性逐渐复杂情况下, ENDA, KLDA比NNDA分类投影后数据分开, 抽取特征更明显。ENDA与KLDA投影效果差别不大, 但KLDA的不足表现在对数据集规模较大样本, 计算时间和空间复杂度变大。综上所述ENDA可作为一种极速且稳定的可视化工具, 其原理简单直观, 通过可视化可以更加了解数据的内在特性, 同时在判别分析时提取最大特征, 不仅降低数据中的不相关和冗余信息, 同时有利于数据的后续分类。
3.3 性能分析对KLDA, NNDA, ELM和ENDA这4种相关算法进行实验对比, NNDA, ELM和ENDA隐层节点设置为相同参数, 采用统计测试集数据分类的错误率和时间进行对比分析。实验结果为10次测试结果平均值和标准差, 如表 2所示。其中错误率公式为
| $ {\rm{ErrorRate}} = \frac{{{\rm{NumError}}}}{{{\rm{NumAll}}}} $ | (14) |
| 表 2 错误率和耗时比较 Tab. 2 Comparisons of classification error rate and training time |
表 2中*代表溢出, 性能较好结果用粗体标出, 虽然ELM是4种方法里最快速的, 但ENDA的分类性能相比ELM得到很大提升。从综合情况看, 当数据规模逐渐变大的情况下, ENDA算法始终表现出较好分类精度和快速性。分析原因如下:(1)实验中发现NNDA需要训练多层神经网络权重和偏置, 导致学习效率低、开销大; NNDA双隐层网络结构致使参数增多, 而ENDA通过随机映射简化了模型结构, 只需要优化LDA层权重, 就可以达到比NNDA更好的效果。(2)NNDA不仅时间花费巨大, 而性能并没有得到改善, 从表 2中ENDA和NNDA分类结果可以看出, ENDA性能更优。由于NNDA在最后一个隐层到输出层训练出的权重并没发挥训练作用, 而且NNDA为了防止变形严重用线性函数替代了Sigmoid函数, 导致学习效果不理想。
从表 2中耗时结果可看出, ENDA比KLDA计算更快速。随着数据集规模增大, 除了Wine数据集外, ENDA的表现明显, 准确性更高。这是因为KLDA隐节点数与训练样本数呈线性关系(计算复杂度为N3), 需要计算N×N大小的核矩阵, 而ENDA只与隐节点数的大小呈线性关系, 只需计算N×L大小的核矩阵, 而隐节点参数L通常远小于N, 当数据规模变大时, KLDA计算成本较高甚至溢出, 而ENDA则表现出更好的可伸缩性。
综上所述, ENDA比NNDA, KLDA更具有极速性, 这充分表明随机映射在不影响分类性能前提下大幅度降低了NN的复杂性。与KLDA不同的是, ENDA, NNDA, ELM都充分发挥了NN的万能逼近能力, 而ENDA不仅强化了随机映射, 而且能保证全局最优解析解, 使学习更加迅速和鲁棒。
4 结束语本文探讨了LDA三种非线性化方法。受随机映射启发, 将NNDA进行改造, 提出ENDA算法, 避免了NNDA需要迭代的调整权重和易陷入局部最优等问题, 并且具有KLDA的全局最优特性, 同时又避免了KLDA对样本依赖的影响, 使其更具极速性和鲁棒性。
由于ENDA随机设置权重和偏置带来的不稳定性, 很容易联想到集成的学习方法, 利用对样本数据进行重采样技术[27-28]加强分类器泛化性能, 对于同质或异质个体学习器集成学习, 可使整个模型决策更加智能化。通常对产生的个体学习器进行集成的学习算法涉及稀疏修剪或多样性的度量相关[29]。多样性度量能确保信息完整性, 而稀疏化建立原则是在不使用更多的个体学习器的情况下就能达到剪枝的目的。Yin等人[30]提出同时结合稀疏正则化和多样性度量这两种方法用于凸二次规划求解, 极大地改进了集成泛化性能, 并有利于大规模数据的并行分布式表示[31-32], 具有很好的扩展性, 这将是下一步研究内容。
| [1] |
杜海顺, 张平, 张帆. 一种基于双向2DMSD的人脸识别方法[J]. 数据采集与处理, 2010, 25(3): 369-372. Du Haishun, Zhang Ping, Zhang Fan. Face recognition method based on bidirectional two-dimensional maximum scatter difference[J]. Journal of Data Acquisition and Processing, 2010, 25(3): 369-372. |
| [2] |
牛璐璐, 陈松灿, 俞璐. 线性判别分析中两种空间信息嵌入方法之比较[J]. 计算机科学, 2014, 41(2): 49-54. Niu Lulu, Chen Songcan, Yu Lu. Comparison between two approaches of embedding spatial information into linear discriminant analysis[J]. Computer Science, 2014, 41(2): 49-54. |
| [3] |
Zhang X Y, Huang K, Liu C L. Feature transformation with class conditional decorrelation[C]//2013 IEEE 13th International Conference on Data Mining. Dallas, Texas: IEEE, 2013: 887-896.
|
| [4] |
Izenman A J. Linear discriminant analysis[M]. New York: Springer, 2013: 237-280.
|
| [5] |
Baudat G, Anouar F. Generalized discriminant analysis using a kernel approach[J]. Neural Computation, 2000, 12(10): 2385-2404. DOI:10.1162/089976600300014980 |
| [6] |
Wang R, Chen X. Manifold discriminant analysis[C]//IEEE Conference on Computer Vision and Pattern Recognition, 2009, CVPR 2009. Anchorage, Alaska: IEEE, 2009: 429-436.
|
| [7] |
Stuhlsatz A, Lippel J, Zielke T. Feature extraction with deep neural networks by a generalized discriminant analysis[J]. Neural Networks and Learning Systems, IEEE Transactions on, 2012, 23(4): 596-608. DOI:10.1109/TNNLS.2012.2183645 |
| [8] |
Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(7553): 436-444. DOI:10.1038/nature14539 |
| [9] |
Wu L, Shen C, Hengel A V D. Deep linear discriminant analysis on fisher networks:A hybrid architecture for person reidentification[J]. Pattem Recognition, 2016, 65: 238-250. |
| [10] |
Mao J, Jain A K. Artificial neural networks for feature extraction and multivariate data projection[J]. Neural Networks, IEEE Transactions on, 1995, 6(2): 296-317. DOI:10.1109/72.363467 |
| [11] |
Hassoun M H. 1996 IEEE transactions on neural networks outstanding paper award[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1996(4): 802-802. |
| [12] |
Scholkopft B, Mullert K R. Fisher discriminant analysis with kernels[J]. Neural Networks for Signal Processing Ⅸ, 1999, 1: 1. |
| [13] |
Cai D, He X, Han J. Speed up kernel discriminant analysis[J]. The VLDB Journal, 2011, 20(1): 21-33. DOI:10.1007/s00778-010-0189-3 |
| [14] |
Sermanet P, Eigen D, Zhang X, et al. Overfeat:Integrated recognition, localization and detection using convolutional networks[J]. arXiv Preprint arXiv, 2013, 1312. |
| [15] |
Hinton G, Deng L, Yu D, et al. Deep neural networks for acoustic modeling in speech recognition:The shared views of four research groups[J]. IEEE Signal Processing Magazine, 2012, 29(6): 82-97. DOI:10.1109/MSP.2012.2205597 |
| [16] |
Collobert R, Weston J, Bottou L, et al. Natural language processing (almost) from scratch[J]. The Journal of Machine Learning Research, 2011, 12: 2493-2537. |
| [17] |
Huang G B, Wang D H, Lan Y. Extreme learning machines:A survey[J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122. DOI:10.1007/s13042-011-0019-y |
| [18] |
Hu G, Peng X, Yang Y, et al. Frankenstein:Learning deep face representations using small data[J]. IEEE Trans Image Process, 2017, 27(1): 293-303. |
| [19] |
Arriaga R I, Rutter D, Cakmak M, et al. Visual categorization with random projection[J]. Neural Computation, 2015, 27(10): 2132. DOI:10.1162/NECO_a_00769 |
| [20] |
刘金勇, 郑恩辉, 陆慧娟. 基于聚类和微粒群优化的基因选择方法[J]. 数据采集与处理, 2014, 29(1): 83-89. Liu Jinyong, Zheng Enhui, Lu Huijuan. Gene selection based on clustering method and particle swarm optimazition[J]. Journal of Data Acquisition and Processing, 2014, 29(1): 83-89. |
| [21] |
Huang G B, Zhu Q Y, Siew C K. Extreme learning machine: A new learning scheme of feedforward neural networks[C]//Proc IJCNN. Budapest, Hungary: [s. n. ], 2004(2): 985-990.
|
| [22] |
Tang J, Deng C, Huang G B. Extreme learning machine for multilayer perceptron[J]. IEEE Transactions on Neural Networks and Learning Systems, 2016, 27(4): 809-821. DOI:10.1109/TNNLS.2015.2424995 |
| [23] |
Huang G B, Zhu Q Y, Siew C K. Extreme learning machine:theory and applications[J]. Neurocomputing, 2006, 70(1): 489-501. |
| [24] |
Huang G B. What are extreme learning machines? Filling the gap between frank rosenblatt's dream and John von neumann's puzzle[J]. Cognitive Computation, 2015, 7(3): 263-278. DOI:10.1007/s12559-015-9333-0 |
| [25] |
Tang J, Deng C, Huang G B. Extreme learning machine for multilayer perceptron[J]. IEEE Transactions on Neural Networks & Learning Systems, 2016, 27(4): 809-821. |
| [26] |
Kasun L L C, Zhou H, Huang G B, et al. Representational learning with ELMs for big data[J]. IEEE Intelligent Systems, 2013, 28(6): 31-34. |
| [27] |
Breiman L. Bagging predictors[J]. Machine Learning, 1996, 24(2): 123-140. |
| [28] |
Schapire R E, Freund Y, Bartlett P, et al. Boosting the margin:A new explanation for the effectiveness of voting methods[J]. The Annals of Statistics, 1998, 26(5): 1651-1686. DOI:10.1214/aos/1024691352 |
| [29] |
Kuncheva L I, Whitaker C J. Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy[J]. Machine Learning, 2003, 51(2): 181-207. DOI:10.1023/A:1022859003006 |
| [30] |
Yin X C, Huang K, Yang C, et al. Convex ensemble learning with sparsity and diversity[J]. Information Fusion, 2014, 20: 49-59. DOI:10.1016/j.inffus.2013.11.003 |
| [31] |
Wang H, He Q, Shang T, et al. Extreme learning machine ensemble classifier for large-scale data[C]//Proceedings of ELM-2014. Singapore: Springer International Publishing, 2015: 151-161.
|
| [32] |
Van Heeswijk M, Miche Y, Oja E, et al. GPU-accelerated and parallelized ELM ensembles for large-scale regression[J]. Neurocomputing, 2011, 74(16): 2430-2437. DOI:10.1016/j.neucom.2010.11.034 |
 2018, Vol. 33
2018, Vol. 33

