引言

噪声是数据采集、传输及处理等环节不可避免的问题。图像受到噪声污染则是引起图像退化和降质的主要因素，它产生于图像的采集、传输、加工、记录等过程。图像去噪之所以重要，原因是数据噪声广泛存在于各类工程实际问题，如采集环境、采集设备、测量误差及记数误差等。而且噪声是一个比较广泛的概念，有很多类型，都是图像中不希望出现的部分^[1]。噪声的存在，会影响人们对感兴趣内容的观看和接收。因此，图像去噪在雷达探测、光电探测、地质勘探^[2-5]、遥感应用^[6]和医疗影像分析^[7]等领域中均有广泛的应用前景。

由于噪声源的多样性，去噪一直是富有挑战性且十分活跃的研究课题，发展了多种经典去噪方法^[8-26]，如基于深度学习的图像去噪方法^[22]，基于信号滤波的算法^[27]和基于奇异值分解(Singular value decomposition, SVD)的去噪方法^{[13, 28, 29]}。随着压缩感知理论^{[30, 31]}的发展，基于稀疏表示和约束正则化的图像去噪成为图像去噪中的最新发展方向和一项重要的技术途径^[23-26]。大部分噪声具有随机性，而图像信号则在某些变换域中或者梯度域中存在明显的稀疏特性。另外，图像去噪恢复本质上也是一个典型的反问题求解过程, 因此稀疏表示和约束正则化自然成为了图像去噪、去模糊、修复及特征融合等诸多反问题求解的重要途径^[3]。对高斯噪声抑制效果较好的稀疏约束方法有基于三维块匹配方法的去噪技术(Block matching 3D, BM3D)^[32]、K奇异值分解方法(K-singular value decomposition, K-SVD)^[29]和基于全变分(Total variation, TV)^{[8, 33-35]}能量泛函技术的去噪方法等。值得注意的是，部分去噪方法仅对高斯噪声有较好的噪声抑制效果，对于其他类型的噪声，例如椒盐噪声、乘性噪声则效果一般。

由于图像存在某些变换域的稀疏性^[10]，稀疏表示及约束正则化是图像恢复与重建的重要技术途径。其中较为典型的稀疏约束有：多尺度小波变换域的稀疏约束和全变分域的稀疏约束。多尺度小波变换域通过一组过完备正交基对图像进行稀疏表示，在变换域中对图像进行稀疏约束，从而提高图像的恢复质量。然而，由于变换域中对某些系数直接通过硬阈值或者软阈值方法加以收缩，会导致空域中的振铃效应。全变分稀疏约束技术充分考虑到图像的梯度稀疏先验知识，并且能很好地应用于各类噪声的去除中，因此基于全变分能量泛函的去噪技术是一种重要的图像去噪方法分支，并且适用于多种类型噪声的图像去噪问题。然而，基于全变分恢复的图像存在较为严重的阶梯效应^[34], 因此全变分方法出现许多变种，总结起来可以分为下列几类：(1)将差分算子加以推广，例如将横竖两方向的差分算子推广为多方向差分算子^{[35, 36]}，或将差分算子推广为分数阶差分算子^{[37, 38]}；(2)针对稀疏收缩算子加以改进，例如将基于L₁范数的全变分推广为基于L_p伪范数^[39-41]的全变分，提高对图像梯度稀疏性的刻画能力；(3)将一阶差分梯度推广为高阶差分梯度，例如广义全变分正则化^[42]；(4)将像素级别的梯度信息推广为交叠组合梯度信息，从而提高图像平滑区域与边缘区域之间的差异性，并有效抑制全变分的阶梯效应，例如交叠组稀疏全变分技术^[43-45]。

本文根据图像随机噪声的产生机理以及噪声幅度特点，总结了图像噪声的分类。然后详细综述各类基于稀疏表示及正则约束约束的图像去噪技术，分析各类技术的去噪机理及其优缺点，同时介绍了图像去噪的评价指标。最后，总结了各类图像去噪方法并讨论未来图像去噪技术的发展趋势。

1 图像噪声分类

图像噪声种类繁多，根据噪声幅度的概率密度函数(Probability density functions，PDF)分布情况可以分为：高斯噪声(Gaussian noise)，瑞利分布噪声(Rayleigh noise)，均匀分布噪声(Uniform noise)，指数分布噪声(Exponential noise)，椒盐噪声(Salt & Pepper noise)和伽马噪声(Gamma noise)等。一般情况下，最为常见的是频谱均匀分布的高斯白噪声。

按照噪声与有效信号之间的数据依赖关系，可以将噪声分类为加性噪声和乘性噪声。(1)加性噪声：每个像素的噪声不管输入信号的大小，噪声总是分别加入到信号中。(2)乘性噪声：例如光量子噪声、胶片颗粒噪声等，噪声受到信息本身的调制。为便于分析处理，常将被乘性噪声污染的信号取自然对数，从而将乘性噪声转化为加性噪声处理。

由于不同噪声特殊的统计特性，在针对不同的噪声类型时，往往需要进行不同的数学建模。例如去除零均值高斯白噪声时，往往采用L₂范数对数据保真项进行建模。在进行椒盐噪声建模时，保真项的建模则可采用L₁范数。

2 图像的稀疏表示及正则化约束去噪方法 2.1 全变分稀疏正则约束

假设噪声为加性高斯噪声，则基于各向异性TV(Anisotropic TV, ATV)去噪模型建模如下

$ \mathit{\boldsymbol{F}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{F}} \frac{1}{2}\left\| {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{G}}} \right\|_2^2 + \mu {R_{{\rm{ATV}}}}\left( \mathit{\boldsymbol{F}} \right) $

(1)

式中：F∈R^N×N表示由去噪模型恢复出的图像；G∈R^N×N表示被噪声污染的图像；$\frac{1}{2}\parallel \mathit{\boldsymbol{F - G}}\parallel _2^2 $为保真项；R_ATV(F)为各向异性全变分正则项; μ为保真项和正则项的平衡系数；‖·‖ ₂表示矩阵的L₂范数，具体定义为$ \parallel \mathit{\boldsymbol{F}}{\parallel _2} = \sqrt {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {F_{ij}^2} } } $。

若加性噪声为椒盐噪声，由于椒盐噪声具有稀疏统计特性，则数据保真项需要用L₁范数来刻画，数学建模需要修改为

$ \mathit{\boldsymbol{F}} = \arg \mathop {\min }\limits_\mathit{\boldsymbol{F}} \frac{1}{2}{\left\| {\mathit{\boldsymbol{F}} - \mathit{\boldsymbol{G}}} \right\|_1} + \mu {R_{{\rm{ATV}}}}\left( \mathit{\boldsymbol{F}} \right) $

(2)

式中R_ATV(F)定义如下

$ {R_{{\rm{ATV}}}}\left( \mathit{\boldsymbol{F}} \right) = {\left\| {{\mathit{\boldsymbol{K}}_{\rm{h}}} * \mathit{\boldsymbol{F}}} \right\|_1} + {\left\| {{\mathit{\boldsymbol{K}}_{\rm{v}}} * \mathit{\boldsymbol{F}}} \right\|_1} $

(3)

式中:K_h=[－1, 1]; ${\mathit{\boldsymbol{K}}_{\rm{v}}} = \left[\begin{array}{l} -1\\ 1 \end{array} \right] $分别表示横向和纵向差分卷积核; ‖·‖₁表示矩阵的L₁范数，具体定义为$\parallel \mathit{\boldsymbol{F}}{\parallel _1} = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {|{\mathit{\boldsymbol{F}}_{ij}}|} } $; 符号表示卷积操作符。ATV模型假设图像为分片常数，导致去噪结果存在比较严重的阶梯效应。

2.2 四方向全变分稀疏正则约束

传统的全变分模型仅考虑两方向的梯度信息，而四方向全变分(Quadruple total variation，QTV)模型则更加充分考虑了邻域梯度信息^{[35, 36]}。下面用图 1来说明四方向全变分的去噪机理，一个点被重噪声污染的概率远远高于周围4个点都被重噪声污染的概率，因此考虑4个方向的梯度要比只考虑2个方向的梯度信息获得的重构图像效果更好。从图 1(a)中可以看到，传统的二方向全变分模型只能最小化横向和纵向梯度，从而对横向和纵向上的图像噪声加以抑制，但是对45°方向和135°方向的噪声则无能为力。而四方向梯度正则项能压制45°方向和135°方向的噪声，从而提高图像复原的质量。四方向全变分模型正则项定义为

$ {R_{{\rm{QTV}}}}\left( \mathit{\boldsymbol{F}} \right) = {\left\| {{\mathit{\boldsymbol{K}}_{\rm{h}}} * \mathit{\boldsymbol{F}}} \right\|_1} + {\left\| {{\mathit{\boldsymbol{K}}_{\rm{v}}} * \mathit{\boldsymbol{F}}} \right\|_1} + {\left\| {{\mathit{\boldsymbol{K}}_{{\rm{4}}{{\rm{5}}^ \circ }}} * \mathit{\boldsymbol{F}}} \right\|_1} + {\left\| {{\mathit{\boldsymbol{K}}_{{\rm{13}}{{\rm{5}}^ \circ }}} * \mathit{\boldsymbol{F}}} \right\|_1} $

(4)

式中：R_QTV(F)表示四方向全变分正则项；${\mathit{\boldsymbol{K}}_{{\rm{45°}}}} = \left[{\begin{array}{*{20}{c}} 0&{-1}\\ 1&0 \end{array}} \right] $；$ {\mathit{\boldsymbol{K}}_{135°}} = \left[{\begin{array}{*{20}{c}} {-1}&0\\ 0&1 \end{array}} \right]$表示对角线和反对角线差分卷积核。

Wu等人将四方向全变分正则项进一步推广为四方向分数阶全变分稀疏正则项^[38]，即充分发挥了四方向全变分正则项的抗噪能力，又发挥了分数阶差分算子缓解阶梯效应的能力，从而获得更好的去噪效果和更快的收敛速度。

值得注意的是，四方向全变分稀疏正则项还可以和交叠组稀疏正则、L_p伪范数收缩算子结合，组合形成新的稀疏正则约束。

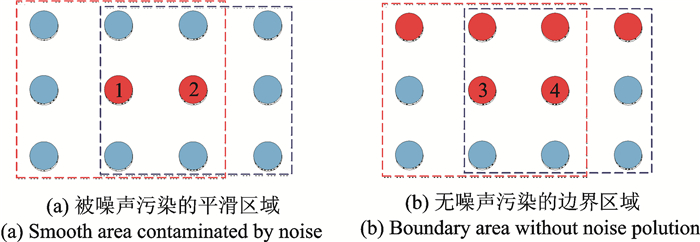
2.3 交叠组稀疏正则约束

近年来，Selesnick和Chen提出了交叠组稀疏正则项(Overlapping group sparse total variation，OGSTV)^[43-45]。该正则项是一种非分离正则项，能更好地保持目标函数的稀疏性^[46]。交叠组稀疏正则项不仅仅考虑到图像差分域的稀疏性，还挖掘了每个点的邻域差分信息，从而挖掘了图像梯度的结构化稀疏特性。通过交叠组合梯度可以提高平滑区域与边界区域的差异，从而抑制TV模型的阶梯效应。Liu等借鉴Selesnick和Chen的工作，将一维交叠组稀疏正则项推广为二维交叠组稀疏正则项，并将其引入各向异性全变分模型，用于椒盐噪声的去噪和解卷积问题中^[47]。Liu等将交叠组稀疏正则项用于Speckle噪声的去除^[48]。交叠组稀疏全变分正则项定义如下^[43-45]

$ {R_{{\rm{OGSTV}}}}\left( \mathit{\boldsymbol{F}} \right) = \varphi \left( {{\mathit{\boldsymbol{K}}_{\rm{h}}} * \mathit{\boldsymbol{F}}} \right) + \varphi \left( {{\mathit{\boldsymbol{K}}_{\rm{v}}} * \mathit{\boldsymbol{F}}} \right) $

(5)

式中：R_OGSTV(F)表示交叠组稀疏正则项；$\varphi \left( \mathit{\boldsymbol{V}} \right) = \sum\limits_{i = 1}^K {\sum\limits_{j = 1}^K {\parallel {{\mathit{\boldsymbol{\tilde V}}}_{i, j, K, K}}{\parallel _2}} } $用于求解组合梯度，${\mathit{\boldsymbol{\tilde V}}} $ _{i, j, K, K}的定义如下

$ {{\mathit{\boldsymbol{\tilde V}}}_{i,j,K,K}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_{i - {K_l},j - {K_l}}}}&{{\mathit{\boldsymbol{V}}_{i - {K_l},j - {K_l} + 1}}}& \cdots &{{\mathit{\boldsymbol{V}}_{i - {K_l},j + {K_r}}}}\\ {{\mathit{\boldsymbol{V}}_{i - {K_l} + 1,j - {K_l}}}}&{{\mathit{\boldsymbol{V}}_{i - {K_l} + 1,j - {K_l} + 1}}}& \cdots &{{\mathit{\boldsymbol{V}}_{i - {K_l} + 1,j + {K_r}}}}\\ \vdots&\vdots&\ddots&\vdots \\ {{\mathit{\boldsymbol{V}}_{i + {K_r},j - {K_l}}}}&{{\mathit{\boldsymbol{V}}_{i + {K_r},j - {K_l} + 1}}}& \cdots &{{\mathit{\boldsymbol{V}}_{i + {K_r},j + {K_r}}}} \end{array}} \right] \in {{\bf{R}}^{K \times K}} $

(6)

式中：K为组合值大小；${K_l} = \left\lfloor {\frac{{K - 1}}{2}} \right\rfloor {\rm{ }};{\rm{ }}{K_r} = \left\lfloor {\frac{K}{2}} \right\rfloor ;{\rm{ }}x $表示小于或等于x的最大整数值。

从式(6)中可以看到，组合梯度$\sum\limits_{i = 1}^K {\sum\limits_{j = 1}^K {\parallel {{\mathit{\boldsymbol{\tilde V}}}_{i, j, K, K}}{\parallel _2}} } $已经将像素点邻域的梯度信息充分考虑，以二范数的方式将这些邻域像素点的梯度信息进行重组，从而提高平滑区域与图像边缘区域之间的差异性。为阐述这个问题，本文给出一个示意图，如图 2所示。假设图 2(a)表示图像的平滑区域的纵向梯度，且①，②两点被噪声重度污染。图 2(b)表示图像中边缘区域的纵向梯度，且无噪声污染，③，④两个像素点表示边缘区域的像素梯度。图 2中蓝色圈表示灰度值较低的像素点，红色圈表示灰度值较高的像素点。为方便讨论，本文假定蓝色区域的灰度值为0，红色区域的灰度值为1。图 2(a)中，如果采用传统的TV去噪方法，由于①，②两个像素点的灰度值与边界处③，④两个像素点梯度值相当，这两点就非常容易被错误地判定为图像边缘并被保留下来，噪声就无法有效去除。在传统TV模型中，讨论的4个点具有完全相同的横向差分和纵向差分。无论阈值取多大，4个点梯度都将出现一致的变化规律。

注意到平滑区域中，连续几个点同时被高噪声污染的概率极小，可以利用这种结构相似性对噪声加以去除。显然，根据式(6)得到的①，②像素的组合梯度为$\sqrt 2 $，而③, ④两个像素的梯度则是$\sqrt 5 $。此时，只要本文将阈值设定为$\sqrt 2 $，①, ②两个像素的噪声就能被很好地去除，与此同时，③, ④两个像素的梯度则被收缩为$\sqrt 5 - \sqrt 2 $，图像边界被很好地保留下来。综上所述，通过交叠组合方式计算像素点梯度时，可以凸显平滑区域的高噪污染点与边界区域像素点的差异性，从而更加鲁棒地进行去噪。利用L₂₁范数收缩算子^[49]来处理组合梯度或者优化最小化(Majorization-minimization，MM)算法^[50]就可以求解交叠组稀疏去噪模型。

2.4 基于L_p伪范数的稀疏全变分正则约束

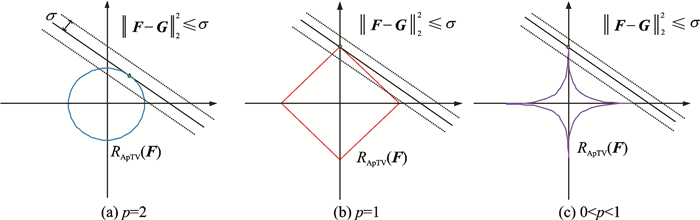
近年来，L_p伪范数^{[41, 51]}的出现已经引起学术界的广泛注意。L_p伪范数相比于L₁范数增加了一个自由度，能更好地刻画稀疏梯度信息。图 3给出基于L₂，L₁，L_p伪范数的各向异性全变分等高线${R_{{\rm{ApTV}}}}\left( \mathit{\boldsymbol{F}} \right)\parallel {\mathit{\boldsymbol{K}}_{\rm{h}}} * \mathit{\boldsymbol{F}}\parallel _p^p + \parallel {\mathit{\boldsymbol{K}}_{\rm{v}}} * \mathit{\boldsymbol{F}}\parallel _p^p\left( {0 < p \le 2} \right) $示意图，其中L₂和L₁范数为L_p范数的特例，L_p范数定义为$\parallel \mathit{\boldsymbol{F}}{\parallel _p} = {(\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {|{\mathit{\boldsymbol{F}}_{ij}}{|^p}} } )^{1/p}} $，L_p伪范数定义为$\parallel \mathit{\boldsymbol{F}}\parallel _p^p = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {|{\mathit{\boldsymbol{F}}_{ij}}{|^p}} } $。图中假设图像被标准差为σ的高斯噪声所污染。可以发现，L₂范数等高线与保真项$\frac{1}{2}\parallel \mathit{\boldsymbol{F - G}}\parallel _2^2 $的交点并不稀疏，而L₁范数等高线与保真项的交点稀疏，但是易受噪声污染。L_p伪范数的等高线则对噪声更加鲁棒。

综上考虑，学者们将基于L₁范数的各向异性全变分推广为如式(7)所示^[40]，并将参数p的范围限定为0＜p＜1。

$ {R_{{\rm{ApTV}}}}\left( \mathit{\boldsymbol{F}} \right) = \left\| {{\mathit{\boldsymbol{K}}_{\rm{h}}} * \mathit{\boldsymbol{F}}} \right\|_p^p + \left\| {{\mathit{\boldsymbol{K}}_{\rm{v}}} * \mathit{\boldsymbol{F}}} \right\|_p^p\;\;\;\;\;\;0 < p < 1 $

(7)

式中R_ApTV(F)表示基于L_p伪范数的各向异性总变分稀疏正则项。

2.5 广义全变分正则约束

前面讨论的各类全变分正则约束都是基于一阶梯度信息的稀疏约束，都一定程度受到阶梯效应的影响。为抑制阶梯效应和提高TV模型的去噪效果，Bredies, Kunisch和Pock提出广义全变分模型(Total generalized variation, TGV)^[42]。二阶广义全变分稀疏正则约束，定义如下

$ \begin{array}{*{20}{c}} {{R_{{\rm{TG}}{{\rm{V}}_2}}}\left( \mathit{\boldsymbol{F}} \right) = \left[ {{\alpha _0}\left( {{{\left\| {{\mathit{\boldsymbol{K}}_{\rm{h}}} * \mathit{\boldsymbol{F}} - {\mathit{\boldsymbol{V}}_x}} \right\|}_1} + {{\left\| {{\mathit{\boldsymbol{K}}_{\rm{v}}} * \mathit{\boldsymbol{F}} - {\mathit{\boldsymbol{V}}_y}} \right\|}_1}} \right) + } \right.}\\ {\left. {{\alpha _1}\left( {{{\left\| {{\mathit{\boldsymbol{K}}_{\rm{h}}} * {\mathit{\boldsymbol{V}}_x}} \right\|}_1} + {{\left\| {{\mathit{\boldsymbol{K}}_{\rm{v}}} * {\mathit{\boldsymbol{V}}_y}} \right\|}_1} + {{\left\| {{\mathit{\boldsymbol{K}}_{\rm{v}}} * {\mathit{\boldsymbol{V}}_x} - {\mathit{\boldsymbol{K}}_{\rm{h}}} * {\mathit{\boldsymbol{V}}_y}} \right\|}_1}} \right)} \right]} \end{array} $

(8)

式中：R_TGV2(F)表示二阶广义全变分正则项，V_x, V_y∈R^N×N；α₀和α₁是控制一阶梯度和二阶梯度的平衡参数。

TGV模型考虑了二阶甚至高阶的梯度信息，能有效抑制阶梯效应。它同时约束了图像的一阶梯度与二阶梯度，从而有效缓解了全变分模型的阶梯效应。该模型是全变分模型的推广，具有凸性、下半连续性、旋转不变性等众多优秀的数学性质，并能逼近任意多项式^[22]，引起学者们的广泛关注，并将TGV正则项应用于众多领域。例如，Knoll, Bredies等将广义全变分模型用于核磁共振成像，取得较好的应用效果^[52]。因此，TGV稀疏正则化技术逐渐成为图像与信号处理领域的新热点。

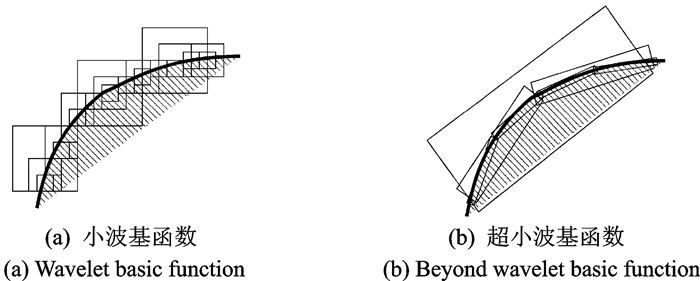
2.6 基于稀疏变换的图像去噪

变换域去噪技术是一种非常常见的去噪技术，这类技术充分考虑到噪声的随机性，从变换域中降低噪声的随机干扰。例如基于小波变换的硬阈值、软阈值技术，先将图像从空域映射到小波域，再对小波系数进行稀疏化操作，最终恢复空域图像。小波变换的小波基函数缺少多尺度、多角度的基函数，对图像细节的刻画能力有限。近年来，超小波的出现逐步弥补了小波变换的缺陷，基于曲波变换(Curvelet transform)^[53]、轮廓波变换(Contourlet transform)^[54]、剪切波变换(Shearlet transform)^[55-57]等超小波的稀疏变换域去噪技术相继出现。图 4展示了超小波基函数与哈尔小波基函数之间的区别。显然，小波基函数对曲线的稀疏表示能力远远低于超小波。

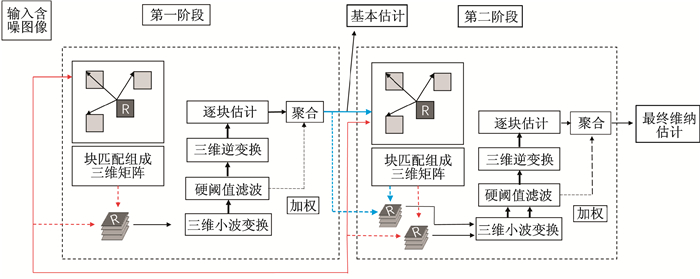
Dabov等提出BM3D算法^[32]，是一种典型的稀疏变换域去噪方法，这种方法主要有两个阶段操作：(1)搜索图像中不同位置的相似块，如图 5中的“R”方块，将相似块组合成三维块矩阵，然后进行三维稀疏变换，在小波变换域中进行硬阈值滤波^[58]，完成图像基本估计；(2)在第一阶段基本估计的基础上，再重新进行块匹配，获得新的三维矩阵，然后结合第一阶段中的三维块矩阵进行小波变换域的协同维纳滤波，最终将三维矩阵进行三维小波逆变换，逐块估计并利用维纳滤波的结果进行加权聚合估计，最后将图像恢复。BM3D的实现框图详见图 5。图 5中，红色实线表示输入的信号为含噪声图像，红色虚线表示由含噪声图像得到的三维块矩阵。蓝色实线表示输入的信号为基本估计图像，蓝色虚线表示由基本估计图像得到的三维块矩阵。

近年来提出的重加权最小核范数(Weighted nuclear norm minimization, WNNM)方法^[59]和基于自适应簇字典的双向低秩表示去噪方法^[60]将图像进行奇异值分解，在变换域中进行奇异值阈值收缩，从而实现图像的去噪，本质上也属于基于稀疏变换的去噪方法。

2.7 基于稀疏字典学习的图像去噪

前面讨论的各类稀疏约束图像去噪技术，尤其是基于变换域的稀疏约束方法，其稀疏表示字典往往是固定的。基于字典学习的稀疏约束图像去噪方法突破了字典固定的局限性。在对图像稀疏表示后，固定稀疏表示系数，然后更新字典，并自适应地学习字典，使得字典对图像的稀疏表示能力得以提高。图 6给出3种字典，其中图 6(a，b)是离散余弦变换(Discrete cosine transform, DCT)字典和哈尔小波字典，而图 6(c)则是通过K-SVD方法获得的学习字典。通过数据驱动得到的字典能更好地表征图像细节，从而获得更好的稀疏表示结果。

字典学习也是稀疏描述方法的一个核心问题，字典由一些典型的模式或者基本元素组成。在稀疏方法中，为一个图像重建问题学习合适的字典将会获得比固定字典更好的效果。目前，字典学习已经在图像去噪、图像超分辨率重建和图像修复等领域得到很好的应用。字典学习问题简单介绍如下，记P=[p₁, p₂, …, p_M]∈R^m×M，是一个M个列向量组成的数据集。D=[d₁, d₂, …, d_K]∈ R^m×K是一个含K个元素的字典。每个数据向量p_i(表示原图中第i个图像块)可以由字典中少量原子进行稀疏表示，即p_i=Dα_i，其中α_i∈R^K×1。令矩阵G=[α₁, α₂, …, α_N]∈R^K×M。稀疏建模的目的是学习字典D，使得X≈DG，同时要保证对于绝大部分图像块，其线性表示系数α_i是稀疏的。在固定字典D时，对系数矩阵G的计算称为稀疏编码阶段。反过来，固定稀疏矩阵G时，更新字典D的过程就是字典学习阶段。因此，字典学习本质上是稀疏编码和字典更新的交替迭代过程。本文将字典学习的数学建模总结为

$ \left( {{\mathit{\boldsymbol{D}}^ * },{\mathit{\boldsymbol{G}}^ * }} \right) = \mathop {\arg \min }\limits_{\mathit{\boldsymbol{D}},\mathit{\boldsymbol{G}}} \left\| {\mathit{\boldsymbol{DG}} - \mathit{\boldsymbol{P}}} \right\|_2^2 + \mu {\left\| \mathit{\boldsymbol{G}} \right\|_0} $

(9)

式中‖·‖₀为L₀范数，具体表示矩阵或向量中非零元素的个数。基于奇异值分解技术的K-SVD^[29]方法是字典学习的经典方法之一，目前已经广泛应用于图像去噪、超分辨率图像重建等领域。

3 噪声衰减质量评价

数据去噪算法的性能评价方法和量化指标很多，依据不同应用领域强调的评价模型和指标各异。其中，最常用的评价指标有峰值信噪比(Peak signal to noise ratio, PSNR)，结构相似性(Structural similarity, SSIM)，相对误差(Relative error, RE)及实时性等^[61]。PSNR，SSIM及RE如式(10~12)所示。

$ {\rm{PSNR}}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = 10\lg \frac{{{{\left( {\max \left( \mathit{\boldsymbol{X}} \right)} \right)}^2}}}{{\frac{1}{{{N^2}}}\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^N {{{\left( {{X_{ij}} - {Y_{ij}}} \right)}^2}} } }} $

(10)

式中：X是原图；Y是重建图像。

$ {\rm{SSIM}}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = \frac{{\left( {2{u_\mathit{\boldsymbol{X}}}{u_\mathit{\boldsymbol{Y}}} + {{\left( {L{k_1}} \right)}^2}} \right)\left( {2{\sigma _{\mathit{\boldsymbol{XY}}}} + {{\left( {L{k_2}} \right)}^2}} \right)}}{{\left( {u_\mathit{\boldsymbol{X}}^2 + u_\mathit{\boldsymbol{Y}}^2 + {{\left( {L{k_1}} \right)}^2}} \right)\left( {\sigma _\mathit{\boldsymbol{X}}^2 + \sigma _\mathit{\boldsymbol{Y}}^2 + {{\left( {L{k_2}} \right)}^2}} \right)}} $

(11)

式中：u_X为X的平均值；u_Y为Y的平均值；σ_X²为X的方差；σ_Y²为Y的方差；σ_XY为X和Y的协方差。L为图像最大灰度；k₁和k₂是用来维持分母非零的常数。

$ {\rm{RE}}\left( {\mathit{\boldsymbol{X}},\mathit{\boldsymbol{Y}}} \right) = \frac{{{{\left\| {\mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}} \right\|}_2}}}{{{{\left\| \mathit{\boldsymbol{X}} \right\|}_2}}} $

(12)

实际应用中采用哪一种评价方式，则取决于具体需求。

4 结束语

针对图像中的随机噪声，本文重点论述了基于稀疏表示和正则化约束去噪的原理和关键技术。最后给出各种去噪方法的去噪评价指标。

基于稀疏表示的不同去噪方法从不同角度加以考虑。例如四方向全变分域稀疏去噪技术主要考虑了像素相邻4点同时受到重噪声污染的概率较小，以此为出发点来进行去噪。基于L_p伪范数的全变分稀疏约束的图像去噪技术则从梯度的稀疏性角度增强了对图像梯度信息的刻画能力。而广义全变分稀疏约束方法则对一阶梯度进行稀疏约束的同时，再进行了二阶甚至高阶梯度的稀疏约束。交叠组稀疏正则约束则充分考虑了邻域组合梯度，提高平滑区域与边缘区域的差异性。BM3D充分考虑图像的非局部相似信息，进行二阶段的三维协同滤波。从上述讨论可以看到，各种方法的研究出发点不同，其优势也有所不同，甚至可以互补。例如广义全变分正则项就没有考虑到利用L_p伪范数来刻画一阶、二阶梯度信息，因此完全可以考虑将广义全变分正则项与L_p伪范数收缩算子结合起来，形成一种新的正则约束项。Zhang等将这种基于L_p伪范数的新型广义全变分应用于医学层析成像中^[62]。BM3D方法在小波域中进行了硬阈值滤波的操作，不可避免地出现局部的振铃效应，超小波域稀疏约束去噪方法也存在类似问题。而利用各类全变分技术则能够有效压制由硬阈值滤波引起的振铃效应，所以将全变分稀疏约束引入到BM3D或者超小波稀疏约束中也是一种非常好的去噪思路。因此，综合多种稀疏约束方法来进行去噪，效果会更明显。